《常微分方程》课程教学资源（讲义）第五章 线性微分方程组（2/2）

$5.3常系数线性微分方程组的求解 根据线性微分方程组解的结构理论，求解线性微分方程组的关键在于求出对应齐线性微 分方程组的基解矩阵当A)为矩阵函数时，求(5.3)的基解矩阵相当不易：当A)=A为常 数矩阵时，可以用代数方法求出方程组的一个基解矩阵 1.矩阵指数expA的定义和性质 设A为n阶常数矩阵，类似于实数e“的幂级数展开式，定义 e=exp4= m+.61 这里E为n阶单位矩阵，A"为A的m次幂，A°=E,0=1.这级数对于任何n阶矩阵都是 收敛的，因而xpA的定义是有意义的，它为一确定的矩阵.事实上，我们有 间小r答眉+o-夜 m 敛，所以expA有意义，且为一个确定的矩阵. 注12对于任何n阶常数矩阵，4为一个确定的非负实数 进一步，级数1eR 含货做的州6c>0金线鞋数 匙厨，空宫智 川≤c上一致收敛 例3设A为对角矩阵，试求exp At, 解记 a A= 这里未写出的元均为零 根据上定义，计算

96 §5.3 常系数线性微分方程组的求解 根据线性微分方程组解的结构理论，求解线性微分方程组的关键在于求出对应齐线性微 分方程组的基解矩阵.当 A(t) 为矩阵函数时，求(5.3)的基解矩阵相当不易；当 A(t) = A 为常 数矩阵时，可以用代数方法求出方程组的一个基解矩阵. 1.矩阵指数exp A 的定义和性质 设 A 为n 阶常数矩阵，类似于实数 a e 的幂级数展开式，定义 = = ∑ = + + +L+ +L ∞ = ! !2 ! exp 2 0 m A A E A k A e A m k k A (5.15) 这里 E 为 n 阶单位矩阵， m A 为 A 的m 次幂， !0, 1 0 A = E = .这级数对于任何n 阶矩阵都是 收 敛 的 ， 因 而 exp A 的 定 义 是 有 意 义 的 ， 它 为 一 确 定 的 矩 阵 . 事 实 上 ， 我 们 有 ! ! , , k A k A E n A A k k m m = ≤ ≤ ， 而 ( ) A m n e m A A n + A + + + + = −1 + 2! ! 2 L L 收 敛，所以exp A 有意义，且为一个确定的矩阵. 注 12 对于任何n 阶常数矩阵， A 为一个确定的非负实数. 进一步，级数 ∑ ∞ = ∀ ∈ 0 ! , k k k k A t t R 是收敛的，且当 t ≤ c, c > 0 时，此级数是一致收 敛的.事实上，由于 ! ! k! A c k A t k A t k k k k k k ≤ ≤ ，而级数∑ ∞ =0 ! k k k k A c 收敛，于是∑ ∞ =0 ! k k k k A t 在 t ≤ c 上一致收敛. 例 3 设 A 为对角矩阵，试求exp At . 解 记               = an a a A O 2 1 这里未写出的元均为零. 根据上定义，计算

xp At =E 根据定义(5.15)，知expA具有如下性质： (I)若n阶矩阵A和B可交换，即AB=BA,则有expA-expB=exp(A+B): (2)对于任何n阶矩阵A,则(expA存在，且有(expA'=exp(-A): (3)诺T为非奇异矩阵，则有expT-AT)=T-(expA)T 对于常系数齐线性微分方程组， 下”=A家 (5.16) 我们有如下定理 定理9对于方程组(5.16)，则矩阵函数Φ()=expA1为方程组(5.16)的基解矩阵，且 (O)=E.此时称expA为标准基解矩阵 证明事实上，由上面讨论知xpA!在任何有限区间上一致收敛，所以计算有 0=4号+g+ =E++4+ =A) 注意到④(O)=E,可知定理成立，证毕 注13对于常系数齐线性微分方程组(5.16)的通解为)=(expA,这里c为任意n维 常数向量 架首先末标雅军解矩腾e即，时4-6-69日04+么，期阳 9%

97               = +               + +               +               = + a t a t a t m n m m m n n n e e e a a a m t a a a t a a a t At E O L O L O O 2 1 !1 !2 ! exp 2 1 2 2 2 2 1 2 2 1 . 根据定义(5.15)，知exp A 具有如下性质： (1)若 n 阶矩阵 A 和 B 可交换，即 AB = BA，则有exp A⋅ expB = exp(A + B) ； (2)对于任何n 阶矩阵 A ，则( ) 1 exp − A 存在，且有( A) = (− A) − exp exp 1 ； (3)若T 为非奇异矩阵，则有exp(T AT ) T (exp A)T −1 −1 = . 对于常系数齐线性微分方程组， x Ax v v ′ = (5.16) 我们有如下定理. 定理 9 对于方程组(5.16)，则矩阵函数 Φ(t) = exp At 为方程组(5.16)的基解矩阵，且 Φ )0( = E .此时称exp At 为标准基解矩阵. 证明 事实上，由上面讨论知exp At 在任何有限区间上一致收敛，所以计算有 ( ) !2 ! !2 ! ( ) 2 2 3 2 1 2 A t m A t A t A E At m A t A t t A A t m m m m = Φ         = + + + + + Φ′ = + + + + + + L L L L ， 注意到Φ )0( = E ，可知定理成立，证毕. 注 13 对于常系数齐线性微分方程组(5.16)的通解为 t ( At)c v v ϕ( ) = exp ，这里c v 为任意n 维 常数向量. 例 4 试求方程组 x x v v         ′ = 0 2 2 1 的通解. 解 首先求标准基解矩阵 exp At ，此时 1 1 0 0 0 1 0 2 2 0 0 2 2 1 A = A + B         +        =        = ，易知

A和B,是可交换的，由性质(1)知，exp At=cxpA1·cxpB,t 其次分别计算 6mema=+6小8+ 放方程组的都为0)-，这里8为任意草活数有量 2.基解矩阵的计算 下面主要介绍三种计算基解矩阵方法 一，基于特征值和特征向量型计算基解矩阵 类似于一阶齐线性微分方程，我们希望方程组(5.16)有解形如(1)=ec, 这里1为待定的参数，c为待定的n维非零向量，将之代入方程组，得到“e=Ae“e 即有 (2E-A)=0(5.17). 要使齐线性代数方程组(5.17)有非零解向量，应有 det(2E-A)=06.18) 称式子(5.18)为方程组(5.16的特征方程，称入为A的特征值，称非零解向量c为A的对应 于特征值入的特征向量于是我们有如下结论： )=e“c为方程组(5.16)解的充分必要条件是入为A的特征值，且c为对应于1的特征向 量 这样就提供了用代数方法求解的平台. (1)设A具有n个线性无关的特征向量可，2，.，下。，它们对应的特征值分别为 入，入2，.，入n(不必各不相同).易知矩阵 )=（e,ep2,.,epn）1∈R 是常系数齐线性微分方程组（⑤.16）的一个基解矩阵，事实上，由上面讨论知道向量函数 e“气(1≤i≤n)都是(5.16)的一个解.因此()是(5.16的解矩阵，计算 det④(0)=det,2,.,n)≠0，于是p()是(5.16)的基解矩阵 注14当A具有n个不同的特征值时，就满足上述性质. 注15此处Φ()不一定是标准基解矩阵expA1,但由定理7(4)知存在一个n阶非奇异 98

98 A1 和 B1是可交换的，由性质（1）知， At A t B t 1 1 exp = exp ⋅ exp . 其次分别计算         = t t e e A t 2 2 1 0 0 exp 和   +L       +        = + 2 2 1 0 0 0 1 0 0 !2 0 1 exp t B t E t ， 注意到         =         0 0 0 0 0 0 0 1 2 ，于是         = 0 1 1 exp 2 t At e t . 故方程组的通解为 ( ) c t t e v t v         = 0 1 1 2 ϕ ，这里c v 为任意n 维常数向量. 2. 基解矩阵的计算 下面主要介绍三种计算基解矩阵方法： 一. 基于特征值和特征向量型计算基解矩阵 类似于一阶齐线性微分方程，我们希望方程组(5.16)有解形如 t e c v λt v ϕ( ) = ， 这里λ 为待定的参数，c v 为待定的n 维非零向量，将之代入方程组，得到 e c Ae c λt v λt v λ = ， 即有 ( ) 0 v v λE − A c = (5.17). 要使齐线性代数方程组(5.17)有非零解向量，应有 det(λE − A) = 0 (5.18) 称式子(5.18)为方程组(5.16)的特征方程，称λ 为 A 的特征值，称非零解向量c v 为 A 的对应 于特征值λ 的特征向量.于是我们有如下结论： t e c v λt v ϕ( ) = 为方程组(5.16)解的充分必要条件是λ 为 A 的特征值，且c v 为对应于λ 的特征向 量. 这样就提供了用代数方法求解的平台. (1)设 A 具有n 个线性无关的特征向量 n v v v v L v v , , , 1 2 ，它们对应的特征值分别为 λ λ λn , , , 1 2 L （不必各不相同）.易知矩阵 t (e v e v e v n ) t R t t t Φ( ) = 1 1 , 2 2 , , n ∀ ∈ v L λ v λ v λ 是常系数齐线性微分方程组(5.16)的一个基解矩阵.事实上，由上面讨论知道向量函数 e v ( i n) i t i 1 ≤ ≤ λ v 都 是 (5.16) 的 一 个 解 . 因 此 Φ(t) 是 (5.16) 的 解 矩 阵 ， 计 算 det )0( det( , , , ) 0 Φ = v1 v2 vn ≠ v L v v ，于是Φ(t) 是(5.16)的基解矩阵. 注 14 当 A 具有n 个不同的特征值时，就满足上述性质. 注 15 此处Φ(t) 不一定是标准基解矩阵exp At ，但由定理 7（4）知存在一个n 阶非奇异

矩阵C,有expA1=(0C,令1=0，得到C=l(O),即expA1=(U)师(O).于 是当A是实矩阵时，那么xpA为实的，这样上式就给出了一个构造实基解矩阵方法 例5求方程组'=A行 a 其中A= 这里未写出的元均为零 的一个基解矩阵 解显然A是对角矩阵，它有n个特征值入=a(1≤i≤n,对于每个特征值元，易 知对应于其的特征向量为c=(0.1.0),即有（亿，E-A克，=0.而这些特征向量 G,C2,.,Cn线性无关，根据注14，于是方程组有基解矩阵 这与例3中计算结论一样 例6试求方程组 x=， 肿4（到 的一个实基解矩阵， 解A的特征值就是特征方程 的根，解之得到入：=3士51对应于特征值入=3+51的特征向量，计算齐线性代数方程 as-gXq-0 因此口=心是对应于么的转征向量类似地，可以求得对皮于无的特征向量下=A们

99 矩阵C ，有 exp At = Φ(t)⋅C ，令t = 0 ，得到 )0( −1 C = Φ ，即 exp ( ) )0( −1 At = Φ t Φ .于 是当 A 是实矩阵时，那么exp At 为实的，这样上式就给出了一个构造实基解矩阵方法. 例 5 求方程组 x Ax v v ′ = 其中               = an a a A O 2 1 这里未写出的元均为零 的一个基解矩阵. 解 显然 A 是对角矩阵，它有 n 个特征值 a ( i n) λi = i 1 ≤ ≤ ，对于每个特征值λi ，易 知对应于其的特征向量为 ( ) T i i c 0 L 1 L 0 v = ，即有( ) 0 v v λiE − A ci = .而这些特征向量 n c c c v L v v , , , 1 2 线性无关，根据注 14，于是方程组有基解矩阵 ( )               Φ = = a t a t a t n a t a t a t n n e e e t e c e c e c O v L v v 2 1 1 2 1 2 ( ) . 这与例 3 中计算结论一样. 例 6 试求方程组 x Ax v v ′ = ， 其中         − = 5 3 3 5 A 的一个实基解矩阵. 解 A 的特征值就是特征方程 ( ) 6 34 0 5 3 3 5 det 2 = − + = − − − − = λ λ λ λ λE A 的根，解之得到 3 5i λ 2,1 = ± .对应于特征值 3 5i λ1 = + 的特征向量，计算齐线性代数方程 ( ) 0 5 5 5 5 2 1 1 v v =                − − = u u i i λ E A u 因此         = i u 1 α v 是对应于 λ1 的特征向量.类似地，可以求得对应于λ2 的特征向量         = 1 i v β v . 这里α ≠ ,0 β ≠ 0 为任意常数.而         =         = 1 , 1 1 2 i v i v v v 是对应于 1 2 λ ,λ 的两个线性无关的特征

向鞋宽0-%e小-)的-个 基解矩阵.再由注15知，实基解矩阵为 （e je-Y1 (2)设A有k个不同的特征值，乙2，.，乙，它们的重数分别为n,n2,.,n:,其中 +n2+.+n=n那么怎样计算xpA? 回忆高等代数理论，对应于n,重特征值入，的如下线性代数方程组 (2E-An=0(6.19 的解全体构成n维欧几里得空间的一个n,维子空间U,(1≤j≤k),并且n维欧几里得 空间可表示成U,U2,.,Uk的直和，由此对于n维欧几里得空间的每一个向量五，存在唯 一组向量元，西，.，成，这里，∈U,(1≤j≤k),使得分解式为 i=1+2+.+(520) 因此，一方面，对于(5.16)的初始值(0)=元。，应用(520)知存在可，∈U,有 元。=可+可2+.+，注意到空间U,的构造，即知可，是(5.19的解，即有 (2,E-A下=0 因而有 (,E-Am,=0I2n,l≤j≤k) (5.21). Le-in -A 另一方面，-元，E为对角矩阵，因此由例3知xp入，E) 故有eexp(,E)=E,计算

100 向量.根据注 14，于是矩阵 ( ) ( ) ( ) ( ) ( )         Φ = = + − + − ti ti ti ti t t ie e e ie t e v e v 3 5 3 5 3 5 3 5 1 2 1 2 ( ) λ v λ v 就是方程组的一个 基解矩阵.再由注 15 知，实基解矩阵为 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )         − =        − −         =                 = Φ Φ = + − + − − + − + − − t t t t e i i ie e e ie i i ie e e ie At t t ti ti ti ti ti ti ti ti sin 5 cos5 cos5 sin 5 1 1 2 1 1 1 exp ( ) )0( 3 3 5 3 5 3 5 3 5 1 3 5 3 5 3 5 3 5 1 . (2)设 A 有 k 个不同的特征值 λ λ λk , , , 1 2 L ，它们的重数分别为 k n ,n , ,n 1 2 L ，其中 n n n n 1 + 2 +L+ k = .那么怎样计算exp At ？ 回忆高等代数理论，对应于 j n 重特征值λ j 的如下线性代数方程组 ( ) 0 v v E − A u = n j λ j (5.19) 的解全体构成n 维欧几里得空间的一个 j n 维子空间U ( j k ) j 1 ≤ ≤ ，并且 n 维欧几里得 空间可表示成U U Uk , , , 1 2 L 的直和，由此对于 n 维欧几里得空间的每一个向量u v ，存在唯 一组向量 k u u u v L v v , , , 1 2 ，这里u U ( j k ) j ∈ j 1 ≤ ≤ v ，使得分解式为 k u u u u v L v v v = 1 + 2 + + (5.20) 因 此 ， 一 方 面 ， 对 于 (5.16) 的 初 始 值 0 x )0( x v v = ， 应 用 (5.20) 知 存 在 j U j v ∈ v ， 有 k x v v v v L v v v 0 = 1 + 2 + + .注意到空间U j 的构造，即知 j v v 是(5.19)的解，即有 ( ) 0 v v − j = n jE A v j λ . 因而有 ( E A) v 0 ( l n 1, j k) j j l j − = ≥ ≤ ≤ v v λ (5.21). 另一方面，− λ jE 为对角矩阵，因此由例 3 知 ( )               − = − − − t t t j j j j e e e Et λ λ λ λ O exp ， 故有e ( jEt) E t j − λ = λ exp ，计算

(exp At),=(exp Ar)Ev,=(exp At)e/exp(-iEi),=e (exp(A-1E))v, =-球+n-r 所以方程组(5.16)满足初始条件(0)=元，的解()为 0)=(exp4压=(exp4+丐，++)=(exp4, (522) -*4- 同时注意到(exp4A)=(expA)E=(expAt)(exp At)克2.(exp At)),这里 =00.0,=(01.0,.,n=(0.0Y即在上面初始条件中 分别令元。=毛，元。=e2,.,元。=en，应用(522)求得n个解，然后以这n个解作为列即得 exp At 注16当A只有一个特征值时，即入为n重的，因此下∈R”,都有(2E-A节=0这表 明(E-A为零矩阵，则 exp Ar=(expAr)E=(expAiYe"exp(-iEr))=e"exp(A-iE) -4-y (6.23) 注17公式(5.22)是本节主要的公式之一，它表明方程组的任一解都可以经过有限次代数运 算求出 例7若A是例4中的矩阵，求初值问题'=4A优，(O)=元，的解和exp4 解本题用两种方法计算expA1和). 方法一：易知入2=2是的二重特征值，此时A只有一个特征值，根据(523)，计算有 四-空-g-6w0-6e仰g 大2泥4的=，调2，发兵者个子气-图)不 需要分解，根据5.22，有 101

101 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) j n j j n j j t j j t j j t j j A E v n t A E t e E t A E At v At Ev At e Et v e A E t v j j j j j v L v v v v         − − = + − + − + + = = − = − − − 1 1 2 2 !2 ( )!1 exp exp exp exp (exp ) λ λ λ λ λ λ λ λ ， 所以方程组(5.16)满足初始条件 0 x )0( x v v = 的解ϕ(t) v 为 ( ) ( )( ) ( ) ( ) j n i i j k i j t j k j k A E v i t e t At x At v v v At v i j v v v L v v v v         = − = = + + + = ∑ ∑ ∑ − = = = 1 1 0 1 0 1 2 ! ( ) exp exp exp λ ϕ λ (5.22) 同时注意到( ) ( ) (( ) ( ) ( ) ) n At At E At e At e At e v L v v exp exp exp exp exp = = 1 2 ，这里 ( ) ( ) ( ) T n T T e1 1 0 0 ,e2 0 1 0 , ,e 0 L 0 1 v L L v L v = = = .即在上面初始条件中 分别令 n x e x e x e v v L v v v v 0 = 1 , 0 = 2 , , 0 = ，应用(5.22)求得 n 个解，然后以这 n 个解作为列即得 exp At . 注 16 当 A 只有一个特征值时，即λ 为 n 重的，因此 n ∀v ∈ R v ,都有( ) 0 v v E − A v = n λ .这表 明( ) n λE − A 为零矩阵，则 ( ) ( )( ( )) ( ) ( )i n i i t t A E i t At At E At e Et e A E t λ λ λ λ λ = − = = − = − ∑ − = 1 0 ! exp exp exp exp exp (5.23) 注 17 公式(5.22)是本节主要的公式之一，它表明方程组的任一解都可以经过有限次代数运 算求出. 例 7 若 A 是例 4 中的矩阵，求初值问题 0 x Ax, x )0( x v v v v ′ = = 的解和exp At . 解 本题用两种方法计算exp At 和ϕ(t) v . 方法一：易知 2 λ 2,1 = 是的二重特征值，此时 A 只有一个特征值，根据(5.23)，计算有 ( ) ( ) ( )         = ∑ − = + − = = 0 1 1 2 2 ! exp 2 2 1 0 2 t A E e E t A E e i t At e i t t i i t 和特解 ( ) ( ) 0 t exp At x v v ϕ = . 方法二： 2 λ 2,1 = 是 A 的二重特征值，这时n1 = 2 ， 2 R 只有一个子空间U1，         = 2 1 0 ~ ~ x x x v 不 需要分解，根据(5.22)，有

0=e+-2=(） 分取，-日-=9=毛，代入上式a0冲，则a0=⑥=0 所ap=a展0-6)Pw0=ao收 例8考虑方程组 3-11 '=A标这里A=201 1-12 试求满足初始条件(0)=元=x2的解，并求expA1. 解A的特征方程为 -31-111-1 det(E-4)=-21-1=(-2l01-10=(a-1a-2}=0, -111-201-2 入=1，入=2分别为m,=L,m,=2重特征值，为了确定R的子空间U,和U2,根据(5.19)， 首先考虑齐线性代数方程组 2-114 4-Eh=2-114=0, 1-11八4 解得，=1，这里α为任意常数，因此U,是由，张成的一维子空间 其次考虑齐线性代数方程组 (000Y4 (4-2y=-11042=0 (-110八4， 10 解得2=B 1+0 这里B,y为任意常数，因此U,是由元，张成的二维子空间 0(1 g

102 ( ) ( )         + = + − = 2 2 1 2 0 2 ~ ~ ( ) 2 x x xt t e E t A E x e t t v v v ϕ 分别取 0 1 0 2 1 0 , 0 1 x e x e v v v v =        = =         = ，代入上式ϕ(t) v 中，则         =         = 1 , ( ) 0 1 ( ) 2 2 2 1 t t e t e t t ϕ ϕ v v ， 所以 ( )         = = 0 1 1 exp ( ) ( ) 2 1 2 t At t t e t ϕ ϕ v v 和特解 ( ) ( ) 0 t exp At x v v ϕ = . 例 8 考虑方程组 x Ax v v ′ = 这里           − − = 1 1 2 2 0 1 3 1 1 A ， 试求满足初始条件           = = 3 2 1 0 ~ ~ )0( x x x x x v v v 的解，并求exp At . 解 A 的特征方程为 ( ) ( ) ( )( ) 1 2 0 0 1 2 0 1 0 1 1 1 2 1 1 2 2 1 3 1 1 det 2 = − − = − − − = − − − − − − − − = λ λ λ λ λ λ λ λ λE A ， λ1 = ,1 λ2 = 2 分别为n1 = ,1 n2 = 2 重特征值，为了确定 3 R 的子空间U1和U2，根据(5.19), 首先考虑齐线性代数方程组 ( ) 0 1 1 1 2 1 1 2 1 1 3 2 1 v v =                     − − − − = u u u A E u , 解得           = 1 1 0 u1 α v ，这里α 为任意常数，因此U1是由u1 v 张成的一维子空间. 其次考虑齐线性代数方程组 ( ) 0 1 1 0 1 1 0 0 0 0 2 3 2 1 2 v v =                     − − = − u u u A E u 解得           +           = 1 0 0 0 1 1 2 u β γ v ，这里 β,γ 为任意常数，因此U2是由u2 v 张成的二维子空间

(0） 是可=2-元可2=元 根据(522)，有 （- （-x2+x 0 (+G,-元，+x)月 0)=e'Em+e2(E+(A-2Eh2=ex-元+e2x+6-x2+) 2-x 元-元2+元 (1)(0)0) 最后为了得到即41，依次分别令，=0=1，=0为，代入上式，得到三线 (0(0(1 性无关解，(0，p,(),勇()，于是 0+e2 -te2te2 exp4=(@()m,),()=-e'++1k2”e'-e2”e2 （-e'+ere'-e2re2 二，基于哈密顿-凯莱定理型计算expA!. 设，入，.，入n为A的特征值，它们之中可以有相同的，记 B=E,B=14-E) (1≤j≤k)(5.24. 根据式子(5.24)，有两点值得注意： ()P,=Π(4-E)=(仁旷p(4)=0,其中p)=det(E-A)为特征多项式：事实 上，根据特征多项式p)=det(E-A)=1-),因此p()=0 2AD=元D,+P4 (0≤j≤n-1).事实上，根据式子524，有 B=E,P=(M-HE)P,(0≤j≤n-l, 此式改写成 AP=P+P(0≤j≤n-) 即可 103

103 下面对初始值 0 x )0( x v v = 进行分解，有 0 1 2 x u u v v v = + ，即           +           +           =           1 0 0 0 1 1 1 1 0 ~ ~ ~ 3 2 1 α β γ x x x ，于 是           − + =           − = − 3 2 1 1 1 2 2 1 1 2 1 ~ ~ ~ ~ ~ , ~ ~ ~ ~ 0 x x x x x v x x v x x v v ，根据(5.22)，有 ( ) ( ) ( ) ( )           − + + − + + − + +           − = + + − = − 3 2 1 1 3 2 1 1 3 2 1 2 2 1 2 2 1 2 1 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 0 ( ) 2 x x x x t x x x x t x x x e x x t e Ev e E t A E v e x x v t v t v t t ϕ . 最后为了得到exp At ，依次分别令           =           =           = 1 0 0 , 0 1 0 , 0 0 1 0 0 0 x x x v v v 为，代入上式，得到三线 性无关解 ( ), ( ), ( ) 1 2 3 ϕ t ϕ t ϕ t v v v ，于是 ( ) ( ) ( )           − + − − + + − + − = = t t t t t t t t t t t t t e e e e e e t e e te te t e te te At t t t 2 2 2 2 2 2 2 2 2 1 2 3 1 1 exp ϕ ( ) ϕ ( ) ϕ ( ) v v v . 二. 基于哈密顿-凯莱定理型计算exp At . 设λ λ λn , , , 1 2 L 为 A 的特征值，它们之中可以有相同的，记 , ( ) 1( ) 1 0 P E P A E j k j k = j = ∏ − k ≤ ≤ = λ (5.24), 根据式子(5.24)，有两点值得注意： (1) ( ) ( ) n n n n k Pn A k E p A × = = ∏ − = −1 ( ) = 0 1 λ ,其中 p(λ) = det(λE − A)为特征多项式；事实 上，根据特征多项式 ( ) ( ) ∏= = − = − n k p E A k 1 (λ) det λ λ λ ，因此 A n n p = × ( ) 0 . (2) (0 1) APj = λ j+1Pj + Pj+1 ≤ j ≤ n − .事实上，根据式子(5.24)，有 , ( ) (0 1) P0 = E Pj+1 = A − λ j+1E Pj ≤ j ≤ n − ， 此式改写成 (0 1) APj = λ j+1Pj + Pj+1 ≤ j ≤ n − 即可

我们的目的是寻找如下形式的 e-20623 这里r(),53(),.,r()为待定函数 首先对(5.25)两边关于1求导数，有 dexp(Ar)=r()P (5.26 其次用矩阵A乘以(5.25)两边且结合(2)，有 dexpl4)=yn04D,=∑n0l,nP+P）(62n =0 0 最后比较5.26)和(5.27)的同类项系数，有5()，5(0，.，r,()是初值问题 =A5 =r+5 (2≤j≤n) 5(0)=1r,(0)=0 的解。 s d)en 解特征方程det(E-A)=(亿-2}=0 有两个特征值元=2，入3=2,5,5是初值问题 =2r 3=片+2 5(0)=1,5(0)=0 的解，得到r=e2,5=1e”,因此 eo=n0%+oe=r6r8-60 这与例4的结论一样 三.基于约当标准型计算exp4! 根据高等代数理论，对于n阶矩阵A,必存在非奇异的矩阵P,有P-AP=J 这里J其有约当标准型，即 a

104 我们的目的是寻找如下形式的 j n j exp At rj (t)P 1 0 ∑ 1 − = = + (5.25) 这里 ( ), ( ), , ( ) 1 2 r t r t r t L n 为待定函数. 首先对(5.25)两边关于t 求导数，有 ( ) ∑ − = + = ′ 1 0 1 exp ( ) n j j Pj A At r t (5.26). 其次用矩阵 A 乘以(5.25)两边且结合(2)，有 ( ) ∑ ∑ ( ) − = − = = + = + + + + 1 0 1 0 1 1 1 1 exp ( ) ( ) n j n j j j j j Pj Pj A At r t AP r t λ (5.27). 最后比较(5.26)和(5.27)的同类项系数，有 ( ), ( ), , ( ) 1 2 r t r t r t L n 是初值问题      = = ′ = + ′ = − 1 )0( ,1 )0( 0 1 1 1 1 j j j j j r r r r r r r λ λ (2 ≤ j ≤ n) 的解. 例 9 设         = 0 2 2 1 A ，求exp At . 解 特征方程det( ) ( 2) 0 2 λE − A = λ − = 有两个特征值λ1 = ,2 λ2 = 2， 1 2 r r, 是初值问题      = = ′ = + ′ = )0( ,1 )0( 0 2 2 1 2 2 1 2 1 1 r r r r r r r 的解，得到 t t r e r te 2 2 2 1 = , = ，因此         =        +        = + = 0 1 1 0 0 0 1 0 1 1 0 exp ( ) ( ) 2 2 2 1 0 2 1 t At r t P r t P e te e t t t 这与例 4 的结论一样. 三. 基于约当标准型计算exp At . 根据高等代数理论，对于n 阶矩阵 A ，必存在非奇异的矩阵 P ，有 P AP = J −1 这里 J 具有约当标准型，即

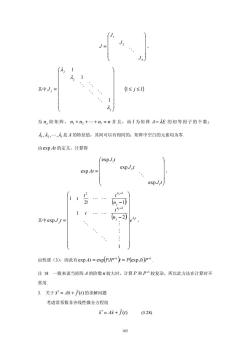
J 其中J, 1sj≤0 。1 为”，阶矩阵，+n2++m=n并且，而1为矩阵A-E的初等因子的个数 入，入，.，入是A的特征值，其间可以有相同的：矩阵中空白的元素均为零 由exp Ar的定义，计算得 expJt exp At= 21 . 11. 其中expJ,1= n,-2e4 1 由性质(3)，因此有exp Al=exp(PP-l=P(expJt)P- 注18一般来说当矩阵A的阶数n较大时，计算P和P-较复杂，所以此方法在计算时不 常用 3.关于'=A标+于)的求解问题 考虑常系数非齐线性微分方程组 =A标+0）(628) 105

105               = n J J J J O 2 1 ， 其中                     = j j j j J λ λ λ 1 1 1 O O O O O (1 ≤ j ≤ l) 为 j n 阶矩阵， n n n n 1 + 2 +L+ l = 并且，而 l 为矩阵 A − λE 的初等因子的个数； λ λ λl , , , 1 2 L 是 A 的特征值，其间可以有相同的；矩阵中空白的元素均为零. 由exp At 的定义，计算得               = J t J t J t At l exp exp exp exp 2 1 O ， 其中 ( ) ( ) t j n j n j j j j e n t t n t t t J t λ                           − − = − − 1 2 ! 1 !2 !1 1 exp 2 2 1 O M O M O M L L L L ， 由性质（3），因此有 ( ) ( ) 1 1 exp exp exp − − At = PJP t = P Jt P . 注 18 一般来说当矩阵 A 的阶数n 较大时，计算 P 和 −1 P 较复杂，所以此方法在计算时不 常用. 3. 关于 x Ax f (t) v v v ′ = + 的求解问题 考虑常系数非齐线性微分方程组 x Ax f (t) v v v ′ = + (5.28)