《离散数学》课程教学资源（PPT课件讲稿）第四章 函数

第四章函数 定义 设f是集合X到Y的关系，如果对每个x∈X, 都存在惟一的y∈Y,使得∈f,则称关系f 为X到Y的函数。 记为f:X→Y。 当∈f时，通常记为y=f(x),这时称x为 函数的自变元，称y为x在f下的函数值。 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 1 第四章 函数 定义 设f是集合X到Y的关系，如果对每个x∈X， 都存在惟一的y∈Y，使得∈f，则称关系f 为X到Y的函数。 记为 f：X→Y。 当∈f时，通常记为y=f(x)，这时称x为 函数的自变元，称y为x在f下的函数值

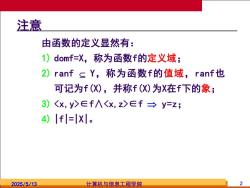
注意 由函数的定义显然有： )domf=X,称为函数f的定义域； 2)ranf Y,称为函数f的值域，ranf也 可记为f(X),并称f(X)为X在f下的象； 3)∈f∧∈f→y=z; 4)1f=X。 2025/5/13 计算机与信息工程学院 2

2025/5/13 计算机与信息工程学院 2 注意 由函数的定义显然有： 1) domf=X，称为函数f的定义域； 2) ranf  Y，称为函数f的值域，ranf也 可记为f(X)，并称f(X)为X在f下的象； 3) ∈f∧∈f  y=z； 4) |f|=|X|

例1 判断下图所示的几个关系是否是函数： B B -B B B 4 B 100a 100a 1O。Oa 100a ○a Ob 20 ○b Ob 2Q 06 20 30 30 30 O 30 40 40 4 40 od Oe 60 h( 6 50 X × 解因f,中X的元素5没出现在序偶的第一元素中， f2中X的元素4出现在两个不同序偶的第一元素中。 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 3 例1 判断下图所示的几个关系是否是函数： 解 因f1中X的元素5没出现在序偶的第一元素中， f2中X的元素4出现在两个不同序偶的第一元素中。 × × √ √ √ √

函数与关系的差别 从定义知，函数确是一种特殊的关系，它与一般 关系比较具备如下差别： )AXB的任何一个子集，都是A到B的二元关系， 因此，从A到B的不同的关系有2lA×B个；但从 A到B的不同的函数却仅有BIA个。 2)每一个函数的基数都为A个，但关系的基数 却可以从零一直到IAXB。 3)每一个函数中序偶的第一个元素一定是互不相 同的。 2025/5/13 计算机与信息工程学院 4

2025/5/13 计算机与信息工程学院 4 从定义知，函数确是一种特殊的关系，它与一般 关系比较具备如下差别： 函数与关系的差别 1) A×B的任何一个子集，都是A到B的二元关系， 因此，从A到B的不同的关系有2 |A||B|个；但从 A到B的不同的函数却仅有|B||A|个。 2) 每一个函数的基数都为|A|个，但关系的基数 却可以从零一直到|A|×|B|。 3) 每一个函数中序偶的第一个元素一定是互不相 同的

例2 设A={a,b},B={1,2},AXB={,, ,}, 此时从A到B的不同关系有24=16个。分别如下： R=Φ；R1={Ka,1>};R2={Ka,2>};R3={Kb,1>}; R4={Kb,2>};R={Ka,1>,};R6={Ka,1>,}; R2=[Ka,2>,};Rg={Ka,2>,}; R3={Ka,1>,};R10={Kb,1>,}; R11={Ka,1>,,};R12={Ka,1>,,}; R13=Ka,1>,,};R14={Ka,2>,,}; R15={Ka,1>,,,}。 2025/5/13 计算机与信息工程学院 5

2025/5/13 计算机与信息工程学院 5 设A＝{a,b}，B＝{1,2}，A×B＝{,, ,}， 例2 此时从A到B的不同关系有2 4＝16个。分别如下： R0＝Φ；R1＝{}；R2＝{}；R3＝{}； R4＝{}；R5＝{,}；R6＝{,}； R7＝{,}；R8＝{,}； R3＝{,}；R10＝{,}； R11＝{,,}；R12＝{,,}； R13＝{,,}；R14＝{,,}； R15＝{,,,}

从A到B的不同的函数仅有22=4个。分别如下： f1={Ka,1>,b,1>};f2={Ka,1>,};f3 =[Ka,2>,};f4={Ka,2>,}。 2025/5/13 计算机与信息工程学院 6

2025/5/13 计算机与信息工程学院 6 从A到B的不同的函数仅有2 2＝4个。分别如下： f1＝{,}；f2＝{,}；f3 ＝{,}；f4＝{,}

定义 设f:A→B,g:C→D,若A=C,B=D,且对 每一x∈A,有f(x)=g(x),则称函数f等于g,记 为f=g。 定义设X和Y是集合，把所有从X到Y的函数构 成的集合记为 Yx={flf:X→Y] 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 7 定义 设f:A→B，g:C→D，若A=C，B=D，且对 每一xA，有f(x)=g(x)，则称函数f等于g, 记 为f=g。 定义 设 X和Y是集合，把所有从X到Y的函数构 成的集合记为 Y X＝｛f|f：X→Y}

定义 设f是从X到Y的函数，若f满足： 对任意x1,x2∈X,若x1≠2，则f(x1)卡f(x2),则 称f为从X到Y的单射； 若ranf=Y,则称f为从X到Y的满射； 若f即是从X到Y的满射，又是从X到Y的单射，则称 f为从到Y的双射。 2025/5/13 计算机与信息工程学院 8

2025/5/13 计算机与信息工程学院 8 定义 设f是从X到Y的函数，若f满足： 对任意x1,x2∈X，若x1≠x2，则f(x1)≠f(x2)，则 称f为从X到Y的单射； 若ranf＝Y，则称f为从X到Y的满射； 若f即是从X到Y的满射，又是从X到Y的单射，则称 f为从X到Y的双射

4)若X=Y,则称f为X上的函数； 5)若X=Y,且对任意x∈X,f(x)=x,则称f为X 上的恒等函数，记为lx 6)若存在b∈Y,且对任意x∈X,f(x)=b,则称 f为常值函数。 2025/5/13 计算机与信息工程学院 9

2025/5/13 计算机与信息工程学院 9 4）若X＝Y，则称f为X上的函数； 5）若X＝Y，且对任意x∈X,f(x)＝x,则称f为X 上的恒等函数，记为IX。 6）若存在b∈Y，且对任意x∈X,f(x)＝b,则称 f为常值函数

例3 确定如下关系哪些关系是函数，若是函数，是 否是单射、满射、双射。 1)设X={1,2,3,4,5},Y={a,b,c,d,e}。 f1={K1,a>,,,,}; f2={K1,a>,,}; f3={K1,a>,,,,}; f4={K1,a>,,,,]o 2025/5/13 计算机与信息工程学院 10

2025/5/13 计算机与信息工程学院 10 确定如下关系哪些关系是函数，若是函数，是 否是单射、满射、双射。 1) 设X＝{1,2,3,4,5},Y＝{a,b,c,d,e}。 f1＝{,,,,}； f2＝{,,}； f3＝{,,,,}； f4＝{,,,,}。 例3