《离散数学》课程教学资源（PPT课件讲稿）第六章 图论

第六章图论 定义一个图是一个序偶,记为 G=,其中： 1)V={1,2,3,V}是一个有限的非空集合， V:（i=1,2,3,n)称为结点，简称点，V为结 点集； 2）)E={e1,e2,e3,em}是一个有限的集合， e:(i=1,2,3,m)称为边，E为边集，E中的 每个元素都有V中的结点对与之对应。即对任 意e∈E,都有e与或者(u,v)相对应。 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 1 定义一个图是一个序偶，记为 第六章 图论 G＝，其中： 1) V＝{v1,v2,v3,.,vn}是一个有限的非空集合， vi(i＝1,2,3,.,n)称为结点,简称点，V为结 点集； 2) E＝{e1,e2,e3,.,em}是一个有限的集合， ei(i＝1,2,3,.,m)称为边，E为边集，E中的 每个元素都有V中的结点对与之对应。即对任 意e∈E，都有e与或者(u,v)相对应

图的分类（按边的方向） 若边e与无序结点对(u,v)相对应，则称边e为无向边，记 为e=(u,v),这时称u,v是边e的两个端点； 若边e与有序结点对相对应，则称边e为有向边（或 弧)，记为e=,这时称u是边e的始点（或弧 尾).v是边e的终点（或弧头），统称为e的端点； 每条边都是无向边的图称为无向图； 每条边都是有向边的图称为有向图； 有些边是无向边，而另一些是有向边的图称为混合图。 用小圆圈表示V中的结点，用由u指向v的有向线段表示 ,无向线段表示(u,V)。 2025/5/13 计算机与信息工程学院 2

2025/5/13 计算机与信息工程学院 2 若边e与无序结点对(u，v)相对应，则称边e为无向边,记 为e＝(u，v)，这时称u，v是边e的两个端点； 若边e与有序结点对相对应，则称边e为有向边(或 弧)，记为e＝，这时称u是边e的始点(或弧 尾).v是边e的终点(或弧头)，统称为e的端点； 每条边都是无向边的图称为无向图； 每条边都是有向边的图称为有向图； 有些边是无向边，而另一些是有向边的图称为混合图。 图的分类(按边的方向) 用小圆圈表示V中的结点，用由u指向v的有向线段表示 ，无向线段表示(u,v)

例 设图G=如右图所 e6 示。这里 es es V={V1,V2,3,V4s}, E={e1,e2,eg,e4e5,e6}, 基粤w2,=g>,9g=, e4=(V2,3),e5=,e6=(V3,3)。 图中的e1、e3e4是无向边，e2e5是有向边。 2025/5/13 计算机与信息工程学院 3

2025/5/13 计算机与信息工程学院 3 例 设图G＝如右图所 示。这里 V＝{v1 ,v2 ,v3 ,v4 ,v5 }， E＝{e1 ,e2 ,e3 ,e4 ,e5 ,e6 }， 其中 e1 ＝(v1 ,v2 )，e2 ＝，e3 ＝(v1 ,v4 )， e4 ＝(v2 ,v3 )，e5 ＝，e6 ＝(v3 ,v3 )。 图中的e1、e3、e4是无向边，e2、e5是有向边

例 G G 上图所示的三个图分别表示为： G,== G2==,, ,}> G3=V3,E3>=,(1,4),, ,}> 2025/5/13 计算机与信息工程学院 4

2025/5/13 计算机与信息工程学院 4 例 上图所示的三个图分别表示为： G1 ＝＝ G2 ＝＝,, ,}> G3 ＝＝,(1,4),, ,}>

几个概念 在一个图中，关联结点v和v的边e, 无论是有向的还是 无向的，均称边e与结点v,和v相关联，而v和v称为 邻接点，否则称为不邻接的； 2)关联于同一个结点的两条边称为邻接边： 3》)图中关联同一个结点的边称为环（或自回路）； 4)图中不与任何结点相邻接的结点称为孤立结点； 5)仅由孤立结点组成的图称为零图； 6)仅含一个结点的零图称为平凡图； e6 )含有n个结点、m条边的图 称为(n,m)图； e2 e 2025/5/13 计算机与信息工程学院 5

2025/5/13 计算机与信息工程学院 5 在一个图中，关联结点vi和vj的边e，无论是有向的还是 无向的，均称边e与结点vI和vj相关联，而vi和vj称为 邻接点，否则称为不邻接的； 几个概念 2) 关联于同一个结点的两条边称为邻接边； 3) 图中关联同一个结点的边称为环(或自回路)； 4) 图中不与任何结点相邻接的结点称为孤立结点； 5) 仅由孤立结点组成的图称为零图； 6) 仅含一个结点的零图称为平凡图； 7) 含有n个结点、m条边的图 称为(n，m)图；

图的分类（按边的重数） 在有向图中，两个结点间（包括结点自身间）若有同始点 和同终点的几条边，则这几条边称为平行边， 在无向图中，两个结点间（包括结点自身间）若有几条边， 则这几条边称为平行边； 两结点v1,v间相互平行的边的条数称为边(v1,v)或的重数； 含有平行边的图称为多重图； 非多重图称为线图； 无自回路的线图称为简单图。 2025/5/13 计算机与信息工程学院 6

2025/5/13 计算机与信息工程学院 6 在有向图中，两个结点间(包括结点自身间)若有同始点 和同终点的几条边，则这几条边称为平行边， 在无向图中，两个结点间(包括结点自身间)若有几条边， 则这几条边称为平行边； 两结点vi，vj间相互平行的边的条数称为边(vi，vj)或的重数； 含有平行边的图称为多重图； 非多重图称为线图； 无自回路的线图称为简单图。 图的分类(按边的重数)

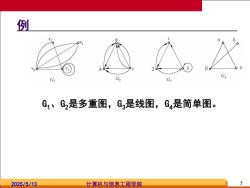
例 G G G1、G2是多重图，G是线图，G4是简单图。 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 7 例 G1、G2是多重图，G3是线图，G4是简单图

图的分类（按权） 定义6.5赋权图G是一个三元组或四元组 N,E,f,g>,其中V是结点集合，E是边的集合，f是从V到 非负实数集合的函数，g是从E到非负实数集合的函数。 非赋权图称为无权图。 50 9 6 6 40 8 9 10 70 35 G G2 2025/5/13 计算机与信息工程学院 8

2025/5/13 计算机与信息工程学院 8 定义6.5 赋权图G是一个三元组或四元组 ，其中V是结点集合，E是边的集合，f是从V到 非负实数集合的函数，g是从E到非负实数集合的函数。 非赋权图称为无权图。 图的分类(按权)

2结点的度数 在无向图G=中，与结点v(vEV)关联的边的条（有 环时计算两次)，称为该结点的度数，记为deg(w); 在有向图G=中，以结点v为始点引出的边的条数， 称为该结点的出度，记为deg(v);以结点v为终点引 入的边的条数，称为该结点的入度，记为deg(v);而 结点的引出度数和引入度数之和称为该结点的度数， 记为deg(v),即deg(w)=deg*(v)+deg(v); 对于图G=,度数为1的结点称为悬挂结点，它所 关联的边称为悬挂边。 在图G=中，称度数为奇数的结点为奇度数结点， 度数为偶数的结点为偶度数结点。 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 9 在无向图G＝中，与结点v(vV)关联的边的条（有 环时计算两次），称为该结点的度数，记为deg(v)； 在有向图G＝中，以结点v为始点引出的边的条数， 称为该结点的出度,记为deg+(v)；以结点v为终点引 入的边的条数，称为该结点的入度,记为deg-(v)；而 结点的引出度数和引入度数之和称为该结点的度数， 记为deg(v)，即deg(v)＝deg+(v)+deg-(v)； 对于图G＝，度数为1的结点称为悬挂结点，它所 关联的边称为悬挂边。 在图G＝中，称度数为奇数的结点为奇度数结点， 度数为偶数的结点为偶度数结点。 2 结点的度数

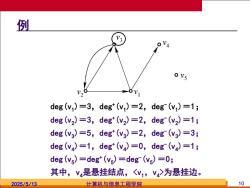
例 o vs 1V deg (v)=3,deg*(v)=2,deg(v)=1; deg(v2)=3,deg*(v2)=2,deg(v2)=1; deg(g)=5,deg*(v3)=2,deg(v3)=3; deg(v4)=1,deg(v4)=0,deg(v4)=1; deg (vs)=deg*(vs)=deg-(vs)=0; 其中，V4是悬挂结点，V1,V4>为悬挂边。 2025/5/13 计算机与信息工程学院 10

2025/5/13 计算机与信息工程学院 10 deg(v1 )＝3，deg+(v1 )＝2，deg-(v1 )＝1； 例 deg(v2 )＝3，deg+(v2 )＝2，deg-(v2 )＝1； deg(v3 )＝5，deg+(v3 )＝2，deg-(v3 )＝3； deg(v4 )＝1，deg+(v4 )＝0，deg-(v4 )＝1； deg(v5 )＝deg+(v5 )＝deg-(v5 )＝0； 其中，v4是悬挂结点，为悬挂边