《离散数学》课程教学资源（PPT课件讲稿）第三章 集合与关系

第三章集合与关系 集合是什么？ “所要讨论的一类对象的整体” “具有同一性质单元的集体” “一些事物汇聚在一起” 常用大写的英文字母A,B,C,.表示 教室里所有的学生 13路公交车 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 1 第三章 集合与关系 集合是什么? “所要讨论的一类对象的整体” “具有同一性质单元的集体” “一些事物汇聚在一起” 常用大写的英文字母A, B, C,.表示 教室里所有的学生 13路公交车

集合的元素 Member /Element 组成一个集合的那些成员称为这个集合的元素。 用a,b,c,.表示集合中的元素 Belong to a是集合A的元素，记以a∈A; a不是集合A的元素，则记以a哇A。 2025/5/13 计算机与信息工程学院 2

2025/5/13 计算机与信息工程学院 2 集合的元素 Member / Element 组成一个集合的那些成员称为这个集合的元素。 用a, b, c,.表示集合中的元素 Belong to a是集合A的元素，记以aA； a不是集合A的元素，则记以aA

集合的表示 ■列举 将集合中的元素一一列举，或列出足够多的元素以 反映集合中元素的特征。 A={0,1,2,3,4,5,6,7,8,9} B=fa,aa,aaa,aaaa,. 谓词描述 用谓词表示集合中元素的性质 A={xk是偶数} 2025/5/13 计算机与信息工程学院 3

2025/5/13 计算机与信息工程学院 3 集合的表示 ◼列举 将集合中的元素一一列举，或列出足够多的元素以 反映集合中元素的特征。 A={0,1,2,3,4,5,6,7,8,9} B={a,aa,aaa,aaaa,.} ◼谓词描述 用谓词表示集合中元素的性质 A={x|x是偶数}

集合的表示 文氏图enn Diagram 用一个大的矩形表示全集，在矩形内画一些圆或其它 的几何图形来表示集合，也可用一些点来表示集合中的特 定元素。 E 常见集合： NQRCZIQR+QR Nm Zm Im E(全集) 空集：⑦不含任何元素的集合称为空集。 2025/5/13 计算机与信息工程学院 A

2025/5/13 计算机与信息工程学院 4 集合的表示 文氏图Venn Diagram 用一个大的矩形表示全集，在矩形内画一些圆或其它 的几何图形来表示集合，也可用一些点来表示集合中的特 定元素。 常见集合: N Q R C Z I Q+ R+ Q- R- Nm Zm Im E(全集) 空集： 不含任何元素的集合称为空集。 A E

子集(subset0 1)设A,B是两个集合，若A的每个元素都是B的元素，则称A是B 的子集，也称B包含A,或A包含于B,记作ACB或B三A。 2)若AcB,且A≠B,则称A是B的真子集(proper subset),也称B真 包含A,或A真包含于B,记作ACB,或BA。 3)若ACB且A三B,称A和B相等，记作A=B。 定义符号化为： B三A←→Vx(x∈B>x∈A) BCA→Vx(x∈B→X∈A)A3x(x∈A∧x庄B) B=A→x(x∈B→x∈A) B不等于A如何符号化？ 2025/5/13 计算机与信息工程学院 5

2025/5/13 计算机与信息工程学院 5 1）设A，B是两个集合,若A的每个元素都是B的元素,则称A是B 的子集,也称B包含A,或A包含于B,记作A  B或B  A 。 2）若AB,且AB，则称A是B的真子集(proper subset),也称B真 包含A,或A真包含于B,记作AB,或B  A 。 3）若A  B且A  B,称A和B相等,记作A=B。 定义符号化为: 子集(subset) B  A  x(x  B → x  A) B =A⇔∀x(x∈B ↔ x∈A) B  A  x(x  B → x  A)  x(x  A  x  B) B不等于A如何符号化?

例 1)设A={2,4,6,8},B={xk是正偶数}， C={xx是整数}，则有A∈B,BC, AcC,并且AcB,BcC,AcC。 2)A如上定义，A有几个子集？ 2025/5/13 计算机与信息工程学院 6

2025/5/13 计算机与信息工程学院 6 1) 设A={2,4,6,8} ，B= {x|x是正偶数}， C={x|x是整数},则有A  B，B C， AC,并且A  B，B  C，A  C 。 2) A如上定义, A有几个子集? 例

重要结论 1)对任意集合A,有ACA。 2)空集是任意集合的子集，且空集是唯一的。（如何 证明？) 3)对于任意两个集合A、B,A=B的充要条件是ACB 且BcA。 4)集合与集合之间是包含与否，元素与集合之间是属 于与否。 2025/5/13 计算机与信息工程学院

2025/5/13 计算机与信息工程学院 7 1)对任意集合A, 有A  A。 2)空集是任意集合的子集，且空集是唯一的。(如何 证明?) 3)对于任意两个集合A、B，A=B的充要条件是AB 且BA。 4)集合与集合之间是包含与否，元素与集合之间是属 于与否。 重要结论

有限集、幂集power set 称含有限个元素的集合为有穷集。用A表示A中 的元素个数。若A=n,则称A为n元集。（集合元 素个数也叫基数、势) n元集合的k元子集有几个？ 设A为一个集合，称A的全部子集组成的集合为 的幂集，P(A)或2A n元集合A的幂集有多少元素？ 2025/5/13 计算机与信息工程学院 8

2025/5/13 计算机与信息工程学院 8 有限集、幂集power set 称含有限个元素的集合为有穷集。用|A|表示A中 的元素个数。若|A|=n，则称A为n元集。(集合元 素个数也叫基数、势) n元集合的k元子集有几个? 设A为一个集合，称A的全部子集组成的集合为 的幂集, P(A) 或 2 A n元集合A的幂集有多少元素?

例 例5.1.1设A={☑}，0,1}，计算A的幂集。 解：P(A)={☑， {☑}，{0}，{1}， {0,{☑}，{1，{0}，{0,1}， {☑}，0,1}} 例5.1.2证明AcB的充要条件P(A)cP(B)。 证明： 充分性。 Vx∈A,有{x}cA。由P(A)cP(B)有{x}CB,所以x∈B, 即AcB。 必要性。 VC∈P(A),有CcA。因为AcB,所以CcB。因此C∈P(B)。 即P(A)cP(B)。 2025/5/13 计算机与信息工程学院 9

2025/5/13 计算机与信息工程学院 9 例 例5.1.1 设A={{}，0，1}，计算A的幂集。 解：P(A)= {, {{}},{0},{1}, {0,{}},{1,{}},{0,1}, {{},0,1} } 例5.1.2 证明AB的充要条件P(A)P(B)。 证明: 充分性。 xA，有{x}A。由P(A)P(B)有{x}B，所以xB， 即 AB。 必要性。 CP(A)，有CA。因为AB，所以CB。因此CP(B)。 即 P(A)P(B)

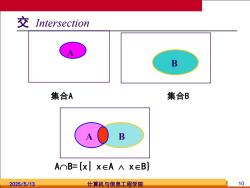
交 Intersection B 集合A 集合B B AOB={xX∈AAX∈B} 2025/5/13 计算机与信息工程学院 10

2025/5/13 计算机与信息工程学院 10 交 Intersection AB={x| xA  xB} A B A B 集合A 集合B