《线性代数》课程教学资源（PPT课件）第三章 矩阵的初等变换及线性方程组 3.3 线性方程组的解

第三节线性方程组的解 一线性方程组引例 二线性方程组的解法 三小结

第三节 线性方程组的解 一 线性方程组引例 二 线性方程组的解法 三 小结

一线性方程组引例 我们考虑： n个未知数m个线性方程所组成的线性方程组 ax1+a12x2+.+ainxn =b a21x1+a22x2+.+a2nxn=b2 台Ax=b amx+am2x2+.+amnxn =bm a11 a12 其中 A= a21 a22 a2n X= b= : am2 ·am Xn

一 线性方程组引例 n个未知数m个线性方程所组成的线性方程组 我们考虑：        + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 , 1 2 21 22 2 11 12 1               = m m mn n n a a a a a a a a a A        , 2 1               = n x x x x                = bm b b b  2 1  Ax = b 其中

n元线性方程组Ax=b, 当常数项b的元素全部为零时，称为n元 齐次线性方程组。 当常数项b的元素不全为零时，称为非 齐次线性方程组

n元线性方程组Ax = b, 齐次线性方程组。 当常数项b的元素全部为零时，称为n元 齐次线性方程组。 当常数项b的元素不全为零时，称为非

引例：求解线性方程组 2x1-x2-x3+x4=2(1) x1+x2-2x3+x4=4(2) (B) 4x1-6x2+2x3-2x4=4(3) 3x1+6x2-9x3+7x4=9(4) 台Ax=b 解：利用消元法， X1+x2-2x3+x4=4(I) (1)→(2) (B)> 2x1-x2-x3+x4=2(2) (B) (3)÷2 2x1-3x2+x3-x4=2(3) 3x1+6x2-9x3+7x4=9(4)

        + − + = − + − = + − + = − − + = (4) (3) (2) ( ) 3 6 9 7 9 4 6 2 2 4 2 4 2 2 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 引例： 求解线性方程组 (B) 解：         + − + = − + − = − − + = + − + = (4) (3) (2) ( ) 3 6 9 7 9 2 3 2 2 2 2 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 利用消元法， (B) →   (1) (2) (3) 2 ( ) B1  Ax = b

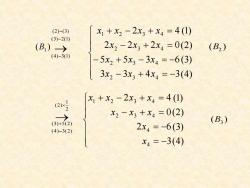
(2)-(3) X1+x2-2x3+x4=4(1) (3)-2(1) (B)→ 2x2-2x3+2x4=0(2) (B2) (4)-3(1) 5x2+5x3-3x4=-6(3) 3x2-3x3+4x4=-3(4) 2x x1+X2-2x3+x4=4(1) x2-X3+x4=0(2) (3)+5(2) (B3) (4)-3(2) 2x4=-6(3) x4=-3(4)

→ − − − (3) 2(1) (2) (3) (4) 3(1) 1 (B )         = − = − − + = + − + = (4) (3) (2) ( ) 3 2 6 0 2 4 4 4 2 3 4 1 2 3 4 x x x x x x x x x ( ) B2 →  − + 2 1 (2) (4) 3(2) (3) 5(2)         − + = − − + − = − − + = + − + = (4) (3) (2) ( ) 3 3 4 3 5 5 3 6 2 2 2 0 2 4 2 3 4 2 3 4 2 3 4 1 2 3 4 x x x x x x x x x x x x x ( ) B3

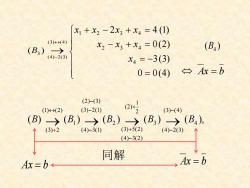
x1+x2-2x3+x4=4(I) (3)>(4) (B3 0> X2-x3+x4=0(2) (B4) (4)-2(3) x4=-3(3) 0=0(4) 一Ax=b (2)-(3) (1)(2) (3)-2(1) (3)-(4) (B)> (B)→(B2)→ (B3)>(B4), (3)÷2 (4)-31) (3)+5(2 (4)-2(3) (4)-3(2) 同解 Ax=b Ax=b

( ) B3 →  − (3) (4) (4) 2(3)         = = − − + = + − + = (4) (3) (2) ( ) 0 0 3 0 2 4 4 2 3 4 1 2 3 4 x x x x x x x x ( ) B4 ( ) ( ) ( ) ( ) ( ), 4 (3) (4) (4) 2(3) 3 2 1 (2) (4) 3(2) (3) 5(2) 2 (3) 2(1) (2) (3) (4) 3(1) 1 (1) (2) (3) 2 B → B → B → B → B − −  − + − − −   同解  Ax = b Ax = b Ax = b

2-1-1 12 11-214 1 1 -2 1 4 01-1 1 0 B=(A,b)= =(A,b) 4 -62 -24 00 01 3 6-97 9 00000 (2)-(3) (1)→(2) (3)-2() a (3)-(4) →(B)>(B2)→(B)→(B4)=(A,b), (3)÷2 (4)-3(1) (3)+52) (4)-2(3) (4)-3(2) 求解Ax=b台求解Ax=b

              − − − − − − = 3 6 9 7 9 4 6 2 2 4 1 1 2 1 4 2 1 1 1 2 ( ) ( ) ( ) ( ) ( , ), 4 (3) (4) (4) 2(3) 3 2 1 (2) (4) 3(2) (3) 5(2) 2 (3) 2(1) (2) (3) (4) 3(1) 1 (1) (2) (3) 2 → B → B → B → B = A b − −  − + − − −   ～ r B= (A,b) 求解Ax = b  求解Ax = b r ( , ) 0 0 0 0 0 0 0 0 1 3 0 1 1 1 0 1 1 2 1 4 = A b               − − −

矩阵初等行变换可以求解线性方程组， 定理：线性方程组经初等变换，解 不变

矩阵初等行变换可以求解线性方程组. 定理：线性方程组经初等变换，解 不变

二、线性方程组的解法 用初等变换求解Ax=b: ①B=(A,b)”→(A,b):行最简形，求R(A),R(B) ②判别（定理1）： R(A)KR(B),则Ax=b无解。 R(4)=R(B,则有解F有唯一解。 <n,有无穷多个解。 ③ x=的解即是Ax=b的解

二、线性方程组的解法 用初等变换求解Ax = b： B (A,b) (A,b) : R(A), R(B). = ⎯r → 行最简形，求 R(A)R(B),则Ax = b无解。   = = 有无穷多个解。 有唯一解。 则有解 , , ( ) ( ), n n R A R B  Ax = b的解即是Ax = b的解。 ① ② ③ 判别（定理1）：

定义：Ax=b的解集表达式称为其通解。 例1求解齐次线性方程组 x1+2x2+x3+x4=0 2x1+x2-2x3-2x4=0. 人x1-七2-4x3-3x4=0 解 对系数矩阵A施行初等行变换： 221 1221 A=21-2-2 5-2 0-3 -6-4 1-1-4-3 3-i 0-3-6-4

例1 求解齐次线性方程组 . 4 3 0 2 2 2 0 2 0 1 2 3 4 1 2 3 4 1 2 3 4      − − − = + − − = + + + = x x x x x x x x x x x x 解           − − − = − − 1 1 4 3 2 1 2 2 1 2 2 1 A           − − − − − − 0 3 6 4 0 3 6 4 1 2 2 1 对系数矩阵 A施行初等行变换： 3 1 2 2 1 r r r r − − 定义：Ax = b的解集表达式称为其通解