《线性代数》课程教学课件（PPT讲稿）第一章 行列式 1-7 n阶行列式

线性代教教程 第一章阶行列式 第七节n阶行列式 一、齐次与非齐次线性方程组的概念 二、克拉默(Cramer)法则 三、重要定理 四、小结、思考题

线性代数教程 线性代数小组 第一章 n阶行列式 第七 节 n阶行列式 一、齐次与非齐次线性方程组的概念 四、小结、思考题 三、重要定理 二、克拉默(Cramer)法则

线性代数教程 第一章阶行列式 一、齐次与非齐次线性方程组的概念 a11X1+412x2+.+1mxn=b1 设线性方程组 21x1+22x2+.+2nxn=b2 mx1+an2x2+.+amxn=bn 若常数项，b2,b不全为零，则称此方程组为非 齐次线性方程组；若常数项b,b2,b,全为零， 此时称方程组为齐次线性方程组

线性代数教程 线性代数小组 第一章 n阶行列式        + + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 设线性方程组 , , , , 若常数项b1 b2  bn不全为零 则称此方程组为非 齐次线性方程组; , , , , 若常数项b1 b2  bn 全为零 此时称方程组为齐次线性方程组. 一、齐次与非齐次线性方程组的概念

线性代教教程 第一章阶行列式 二、克拉默法则 如果线性方程组 011x1+a12x2+.+a1mxn=b1 21x1+22x2+.+2mXn=b2 () .·.。 anx1+an2x2++amxn=bn 010200 的系数行列式不等于零，即D= 0212. 2m≠0 0n10n2

线性代数教程 线性代数小组 第一章 n阶行列式 二、克拉默法则 如果线性方程组 (1) 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1        + + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b     的系数行列式不等于零，即 n n nn n n a a a a a a a a a D     1 2 21 22 2 11 12 1 =  0

线性代数敖程 第一章阶行列式 那么线性方程组)有解，并且解是唯一的，解 可以表为 -分8-合k8 其中D,是把系数行列式D中第列的元素用方程 组右端的常数项代替后所得到的n阶行列式，即 auav b auma D,= 0ni.anab.n4am

线性代数教程 线性代数小组 第一章 n阶行列式 . D D , , x D D , x D D , x D D x n = = =  n = 2 3 2 2 1 1 其中 是把系数行列式 中第 列的元素用方程 组右端的常数项代替后所得到的 阶行列式，即 Dj D j n n n , j n n , j nn , j , j n j a a b a a a a b a a D      1 1 1 11 1 1 1 1 1 1 − + − + = 那么线性方程组 有解，并且解是唯一的，解 可以表为 (1)

线性代教教程 第一章阶行列式 证明 用D中第列元素的代数余子式4,4，.，A 依次乘方程组(1)的n个方程，得 (aux+anx2++aux)Au=BAv (01x1+a2x2++0nn)A,-bA (（anx,+n2x2十+0 )A=bnA 在把n个方程依次相加，得

线性代数教程 线性代数小组 第一章 n阶行列式 证明 ( ) ( ) ( )       + + + = + + + = + + + = n n nn n nj n nj n n j j n n j j a x a x a x A b A a x a x a x A b A a x a x a x A b A     1 1 2 2 21 1 22 2 2 2 2 2 11 1 12 2 1 1 1 1 依次乘方程组( )的 个方程 得 用 中第 列元素的代数余子式 1 , , , , 1 2 n D j A j A j  Anj 在把 n 个方程依次相加，得

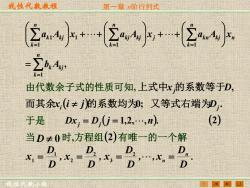
线性代数故程 第一章阶行列式 ②aj小+2小*店小 =∑b4, 由代数余子式的性质可知，上式中x的系数等于D, 而其余x,(i≠的系数均0；又等式右端为D,. 于是 Dx,=D,0=1,2,n) (2) 当D≠0时，方程组(2)有唯一的一个解 8易分8

线性代数教程 线性代数小组 第一章 n阶行列式 , 1 1 1 1 1 1     = = = = =        + +       + +      n k k k j n n k j k n k j n k k j k j n k k k j b A a A x  a A x  a A x 由代数余子式的性质可知, Dx D ( j 1,2, ,n). j = j =  . D D , , x D D , x D D , x D D x n = = =  n = 2 3 2 2 1 1 x D, 上式中 j的系数等于 而其余x (i j)的系数均为0; i  . 又等式右端为Dj 于是 (2) 当 D  0 时,方程组 (2) 有唯一的一个解

线性代教教程 第一章阶行列式 由于方程组(2)与方程组()等价，故 s公%x-0x8 也是方程组的()解

线性代数教程 线性代数小组 第一章 n阶行列式 由于方程组 (2) 与方程组 (1) 等价, 故 . D D , , x D D , x D D , x D D x n = = =  n = 2 3 2 2 1 1 也是方程组的 (1) 解

线性代数敖程 第一章阶行列式 三、重要定理 定理1如果线性方程组(1的系数行列式D≠0， 则()一定有解，且解是唯一的■ 定理2如果线性方程组(1无解或有两个不同的 解，则它的系数行列式必为零

线性代数教程 线性代数小组 第一章 n阶行列式 三、重要定理 定理1 如果线性方程组 的系数行列式 则 一定有解,且解是唯一的 . (1) (1) D  0, 定理2 如果线性方程组 无解或有两个不同的 解，则它的系数行列式必为零. (1)

线性代教教程 第一章阶行列式 齐次线性方程组的相关定理 01X1+412X2+.+01mxn=0 021x1+2x2+.+02nxn=0 (2) 0n1x1+0n2x2+.+0nmxn=0 定理3 如果齐次线性方程组(2)的系数行列式 D≠0则齐次线性方程组（2)没有非零解

线性代数教程 线性代数小组 第一章 n阶行列式 齐次线性方程组的相关定理 (2) 0 0 0 1 1 2 2 21 1 22 2 2 11 1 12 2 1        + + + = + + + = + + + = n n nn n n n n n a x a x a x a x a x a x a x a x a x     定理3 如果齐次线性方程组 的系数行列式 D  0 则齐次线性方程组 没有非零解. (2) (2)

线性代数故程 第一章阶行列式 定理4 如果齐次线性方程组2)有非零解，则它 的系数行列式必为零 系数行列式D=0 011X1+412x2+.+41mxn=0 21X1+22x2+.+42mXn=0 . 0n1x1+n2X2+.+0mmxn=0 有非零解：

线性代数教程 线性代数小组 第一章 n阶行列式 定理4 如果齐次线性方程组 (2) 有非零解,则它 的系数行列式必为零.        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 n n nn n n n n n a x a x a x a x a x a x a x a x a x     有非零解. 系数行列式 D = 0