《线性代数》课程教学课件（PPT讲稿）第一章 行列式 1-2 全排列及其逆序数

线性代数敖程 第-章阶行列式 第二节 全排列及其逆序数 一、概念的引入 二、全排列及其逆序数 三、小结

线性代数教程 线性代数小组 第一章 n阶行列式 第二 节 全排列及其逆序数 一、概念的引入 三、小结 二、全排列及其逆序数

线性代数敖程 第一章阶行列式 一、概念的引入 引例用1、2、3三个数字，可以组成多少个没 有重复数字的三位数？ 解 123 百位 3 3种放法 十位 2 2种放法 个位12 1种放法 共有3×2×1=6种放法

线性代数教程 线性代数小组 第一章 n阶行列式 一、概念的引入 引例 用1、2、3三个数字，可以组成多少个没 有重复数字的三位数？ 解 1 2 3 百位 1 2 3 3种放法 十位 1 2 1 3 个位 1 2 3 2种放法 1种放法 共有 3 21 = 6 种放法

线性代教教程 第一章阶行列式 二、全排列及其逆序数 问题把n个不同的元素排成一列，共有几种不 同的排法？ 定义 把n个不同的元素排成一列，叫做这n个 元素的全排列（或排列）， n个不同的元素的所有排列的种数，通常 用Pn表示 结论：n个元素的全排列共有n!个 nx(n-1)×(n-2)×.×2×1=n!

线性代数教程 线性代数小组 第一章 n阶行列式 二、全排列及其逆序数 同的排法？ 问题 把 n 个不同的元素排成一列，共有几种不 定义 把 个不同的元素排成一列，叫做这 个 元素的全排列（或排列）. n n 个不同的元素的所有排列的种数，通常 用 表示. n Pn 结论：n个元素的全排列共有 n！个 . n n n n  −  −    = ( 1) ( 2) 2 1 !

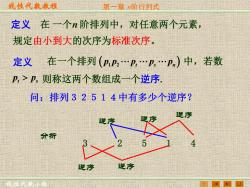
线性代数敖程 第一章阶行列武 定义在一个n阶排列中，对任意两个元素， 规定由小到大的次序为标准次序。 定义在一个排列(pP2.2,.p,.P)中，若数 卫，>P,则称这两个数组成一个逆序 问：排列32514中有多少个逆序？ 逆序 逆序 分析 逆序 逆序

线性代数教程 线性代数小组 第一章 n阶行列式 定义 在 一个n 阶排列中，对任意两个元素， 规定由小到大的次序为标准次序。 在一个排列 中，若数 则称这两个数组成一个逆序. ( p p p p p 1 2 t s n ) t s p p  定义 问：排列３２５１４中有多少个逆序？ 3 2 5 1 4 逆序 逆序 逆序 逆序 分析 逆序

线性代数教程 第一章阶行列式 排列的逆序数 一个排列中所有逆序的总数，称为这个排列 的逆序数，记为：tor.t(pP.P) 排列的奇偶性 逆序数为奇数的排列称为奇排列； 逆序数为偶数的排列称为偶排列， 逆序数为0的排列，称为标准排列

线性代数教程 线性代数小组 第一章 n阶行列式 一个排列中所有逆序的总数， 的逆序数， 称为这个排列 1 2 . . n 记为：t or （p p p ） 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列. 排列的奇偶性 排列的逆序数 逆序数为0的排列，称为标准排列

线性代数故程 第一章阶行列式 例1求下列排列的逆序数，并讨论它们的奇偶性. 1)32514 2)217986354 解1： 32514 ↓↓↓↓↓ t=0+1+0+3+1=5故此排列为奇排列. 解2：21⑦⑨⑧⑥3⑤4 0i001i3445 t=5+4+4+3+1+0+0+1+0=18 故此排列为偶排列

线性代数教程 线性代数小组 第一章 n阶行列式 例1 求下列排列的逆序数，并讨论它们的奇偶性. 1） 3 2 5 1 4 解2： t = 5 = 18 故此排列为偶排列. +4 + 4 + 3 + 1 + 0 + 0 + 1 + 0 2 1 7 9 8 6 3 5 4 0 1 0 0 1 3 4 4 5 2） 2 1 7 9 8 6 3 5 4 解1： t = 0 +1 +0+ 3 +1 3 2 5 1 4 = 5 故此排列为奇排列

线性代教教程 第一章阶行列式 量 计算排列的逆序数，并讨论奇偶性 (2k)(2k-)2(2k-23(2k-3)-(k+1)k 分析01i支支··，k二1长 1k2 当k为偶数时，该排列为偶排列； 当k为奇数时，该排列为奇排列

线性代数教程 线性代数小组 第一章 n阶行列式 (2 1 2 1 2 2 2 3 2 3 1 k k k k k k ) ( − − − + ) ( ) ( ) ( ) 计算排列的逆序数，并讨论奇偶性. 分析  0  1  1  2  2   k 1 k  − 2 t k = 当 k 为奇数时，该排列为奇排列. 当 k 为偶数时，该排列为偶排列；

线性代数教程 第一章阶行列式 三、小结 1.n个不同的元素的所有排列种数为n! 2.排列具有奇偶性

线性代数教程 线性代数小组 第一章 n阶行列式 三、小结 2. 排列具有奇偶性. 1. n个不同的元素的所有排列种数为n!

线性代教教程 第一章阶行列式 思考题 分别用两种方法求排列16352487的逆序数

线性代数教程 线性代数小组 第一章 n阶行列式 思考题 分别用两种方法求排列16352487的逆序数

线性代数赦程 第一章阶行列式 思考题解答 解用方法1 16352487 t-=0+3+1+2+1+0+1+0=8 用方法2由前向后求每个数的逆序数 t=0+0+1+1+3+2+0+1=8

线性代数教程 线性代数小组 第一章 n阶行列式 思考题解答 解 用方法1 1 6 3 5 2 4 8 7 用方法2 t = 0 + 3 + 1+ 2 + 1+ 0 + 1+ 0= 8 由前向后求每个数的逆序数. t = 0 + 0 + 1+ 1+ 3 + 2 + 0 + 1 = 8