《线性代数》课程教学课件（PPT讲稿）第五章 相似矩阵及二次型 第三节 相似矩阵

线性代数教程第0503节相似矩鸭 2347 第三节相似矩阵 一、相似矩阵与相似变换的概念 二、相似矩阵与相似变换的性质 三、利用相似变换将方阵对角化 四、小结思考题 线性代数小组 第1页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第1页 第三节 相似矩阵 一、相似矩阵与相似变换的概念 二、相似矩阵与相似变换的性质 三、利用相似变换将方阵对角化 四、小结 思考题

线性代数教程 第0503节相似矩阵 2347 、相似矩阵与相似变换的概念 定义1设A,B都是n阶矩阵，若有可逆矩阵P,使 P-AP=B, 则称B是A的相似矩阵或说矩阵A与B相似.对A进 行运算PAP称为对A进行相似变换可逆矩阵P 称为把A变成B的相似变换矩阵 线性代数小组 第2页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第2页 一、相似矩阵与相似变换的概念 . , , . , 1 , , , 1 1 称为把 变 成 的相似变换矩阵 行运算 称为对 进行相似变换可逆矩阵 则 称 是 的相似矩阵 或说矩阵 与 相 似 对 进 定 义 设 都 是 阶矩阵 若有可逆矩阵 使 A B P AP A P B A A B A P AP B A B n P − − =

线性代数教程第0503节相似矩阵 2347 二、相似矩阵与相似变换的性质 1.等价关系 ()反身性A与A本身相似 (2对称性若A与B相似，则B与A相似， (3)传递性 若A与B相似，B与C相似， 则A与C相似. 2.P(4A)P-(PAPp1A,P） 3.若A与B相似，则Am与Bm相似m为正整数) 线性代教小组 第3页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第3页 1. 等价关系 2. ( ) ( )( ). 2 1 1 1 1 2 1 P A A P P A P P A P − − − = 3.若A与B相似,则A 与B 相似(m为正整数). m m 二、相似矩阵与相似变换的性质 A与A本身相似. 若A与B相似,则B与A相似. . , , 则 与 相似 若 与 相似 与 相似 A C A B B C (1)反身性 (2)对称性 (3)传递性

线性代数教程 第0503节相似矩阵 2347 4.P-(k A +k24)P=k P-A P+kPA,P 其中k1,飞，是任意常数. 定理1若n阶矩阵A与B相似，则A与B的特征多项 式相同，从而A与B的特征值亦相同 证明A与B相似 →]可逆阵P,使得P-AP=B .B-E=P-AP-P-AE)P =P-(A-AE)P =P-A-E P =A-2E. 线性代数小组 第4页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第4页 证明 A与B相似 B E P AP P (E)P −1 −1  − = − = P (A − E)P −1 = P A− E P −1 = A − E . P (k A k A )P k P A P k P A2P 1 1 2 1 1 1 2 2 1 1 4. − − − + = + , . 其中k1 k2是任意常数   P P AP = B −1 可逆阵 ,使得 , . 1 , 式相同 从 而 与 的特征值亦相同 定 理 若 阶矩阵 与 相 似 则 与 的特征多项 A B n A B A B

线性代数教程第0503节相似矩腾 2347 推论若n阶方阵A与对角阵 相似，则21,22，2即是4的n个特征值 线性代数小组 第5页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第5页 推论 若 n 阶方阵A与对角阵                =  n    2 1 , , , , . 相似 则1 2   n即是A的n个特征值

线性代数教程第0503节相似矩阵 2347 利用对角矩阵计算矩阵多项式 若A=PBP,则 k个 APBP PBP-.PEP-PBPD PBP-. A的多项式 (A)=a0A"+aiA++anA+arE ao P B"P+aP B"-P+. an-PBP+an PE P- P(ao B"+aiB"++anB+ar E)P Po(B)P. 线性代数小组 第6页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第6页 利用对角矩阵计算矩阵多项式 , 1 A PB P − 若 = a PB P a PE P a P B P a P B P n n n n 1 1 1 1 1 1 1 0 − − − − − − + + = + +  A = k A的多项式 A a A a A an A anE n n = + + + − + − 1 1 0 1 ( )  ( ) . 1 P B P − =  . 1 P B P k − = 则 P a B a B an B anE P n n 1 1 1 0 1 ( ) − − − = + ++ + PBP −1 PBP −1 PBP −1 PBP −1 k个

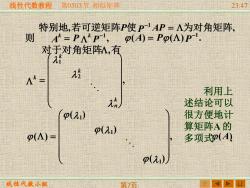
线性代数教程第0503节相似矩阵 2347 特别地，若可逆矩阵P使P1AP=人为对角矩阵， 则 A=P人P-,P(A)=Pp(A)P 对于对角矩阵私，有 1所 2经 利用上 述结论可以 p(2) 很方便地计 p(2) 算矩阵A的 p(A)= 多项式p(A) p() 线性代数小组 第页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第7页 , , 特别地 若可逆矩阵P使P −1 AP = 为对角矩阵 , 1 A P P k k − 则 =  ( ) ( ) . 1 A P P −  =   对于对角矩阵,有 , 2 1                =    k n k k k  , ( ) ( ) ( ) ( ) 1 1 1                =         利用上 述结论可以 很方便地计 算矩阵A 的 多项式 . (A)

线性代数教程 第0503节相似矩阵 2347 定理设f(2)是矩阵A的特征多项式则f()=O, 证明只证明A与对角矩阵相似的情形 若A与对角矩阵相似，则有可逆矩阵P,使 PAP=A=dig21,.,九n, 其中，为A的特征值，f2)=0.由A=PAp,有 f() f(A)=Pf(A)P-=P =P0P1=0. 线性代数小组 第8页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第8页 定理 设f ()是矩阵A的特征多项式,则f (A) = O. 证明 只证明A与对角矩阵相似的情形. 若A与对角矩阵相似,则有可逆矩阵P,使 ( , , ), 1 1 P AP =  = diag    n −  , ( ) = 0. i i 其中 为A的特征值 f 由A = P P −1 ,有 f (A) . 1 = PO P = O − Pf P 1 ( ) − =  P f f P n 1 1 ( ) ( ) −           =   

线性代数教程第0503节相似矩阵 2347 三、利用相似变换将方阵对角化 对n阶方阵A,若可找到可逆矩阵P,使 PAP=△为对角阵，这就称为把方阵A对角化 定理2n阶矩阵A与对角矩阵相似即A能对角化 的充分必要条件是4有n个线性无关的特征向量 证明 假设存在可逆阵靶，使P-AP=人为对角阵， 把P用其列向量表示为P=(p,P2,Pn). 线性代数小组 第9项

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第9页 , . , , 1 为对角阵 这就称为把方阵 对角化 对 阶方阵 若可找到可逆矩阵 使 P AP A n A P =  − 证明 , , 假设存在可逆阵P 使P −1AP = 为对角阵 ( , , , ) . 把 P 用其列向量表示为P = p1 p2  pn 三、利用相似变换将方阵对角化 . 2 ( ) 的充分必要条件是 有 个线性无关的特征向量 定 理 阶矩阵 与对角矩阵相似即 能对角化 A n n A A

线性代数教程第0503节相似矩阵 23:47 由P1AP=A,得AP=PA, 即Ap,P2,pn)=(p1,P2,Pn） 入2 =(1P1,2P2,nPn)） .A(D1,P2,Pn)=(4p1p2,4pn) =(2P1,2P2,1nPn） 于是有 Ap:=1P:（=1,2,) 线性代数小组 笔0页

线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第10页 ( ) ( )               = n n n A p p p p p p       2 1 1 2 1 2 即 , , , , , , ( , , , ). = 1 p1 2 p2   n pn ( ) ( ) A p p pn Ap Ap Apn , , , , , ,  1 2  = 1 2  Ap p (i 1,2, ,n). 于是有 i = i i =  ( )  p  p  n pn , , , = 1 1 2 2  , , 1 =  =  − 由P AP 得AP P