《高等数学》课程授课教案（讲义）第六章 定积分的应用

第六章定积分的应用86.1定积分的元素法教学目的：理解和掌握用定积分去解决实际问题的思想方法即定积分的元素法教学重点：元素法的思想教学难点：元素法的正确运用教学内容：一、再论曲边梯形面积计算设f(x)在区间[a,b]上连续，且f(x)≥0，求以曲线y=f(x)为曲边，底为[a,b]的曲边梯形的面积A。y=f(x)AA,=J(P).AXAbα-01-1、化整为零用任意一组分点a=x<x<<x--<x<..<x,=b将区间分成n个小区间[xi-1,x,]，其长度为Axi = xi - x,-1(i= 1,2,..,n)并记=max[Axi,Ax2,,Ax,)相应地，曲边梯形被划分成n个窄曲边梯形，第i个窄曲边梯形的面积记为AA( i=1,2,,n )。nA=ZAA于是i=1168

168 第六章 定积分的应用 §6.1 定积分的元素法 教学目的：理解和掌握用定积分去解决实际问题的思想方法即定积分的元素法 教学重点：元素法的思想 教学难点：元素法的正确运用 教学内容： 一、再论曲边梯形面积计算 设 f ( ) x 在区间[,] a b 上连续，且 f ( ) x ≥ 0，求以曲线 y = f ( ) x 为曲边， 底为[,] a b 的曲边梯形的面积 A。 1、化整为零 用任意一组分点 a = x0 < x1 <"< xi−1 < xi <"< xn = b 将区间分成 n 个小区间[ ,] x x i i −1 ，其长度为 Δxxx i n i ii = − −1 ( , , ) = 1 2 " 并记 max{ , , , } 1 2 n λ = Δx Δx " Δx 相应地，曲边梯形被划分成 n 个窄曲边梯形，第 i 个窄曲边梯形的面积记为 A ( i 1, 2, , n ) Δ i = " 。 于是 A Ai i n = ∑ = Δ 1

2、以不变高代替变高，以矩形代替曲边梯形，给出“零”的近似值A, ~ f(5)Ax;VEi e[xi-1,xi] (i=1,2,.*,n)3、积零为整，给出“整”的近似值7A~ Zf(5i)Axii=14、取极限，使近似值向精确值转化bA= lim Zf()Ax; =Jf(x)dx→0i=1a上述做法蕴含有如下两个实质性的问题：(一)、若将[a,b]分成部分区间[xi-1,x;](i=1,2,",n)，则A相应地分成部F分量A,(i=1,2,,n)，而 A=≥Ai=1这表明：所求量A对于区间[a,b]具有可加性。(二)、用f(S)Ax近似△A，误差应是△x,的高阶无穷小。n只有这样，和式Zf（Si)Ax；的极限方才是精确值A。i=1故，确定△A,~f(S)Ax,（△A,f(S)Ax=o(Ax))是关键。上述做法可进一步简化为略去下标i，用△A表示任一小区间[x,x+dx】上窄曲边梯形的面积，这样A=ZAyAA的近似值可取作f(x）dxy=f(x)一般地称f(x）dx为面积元素，记作dA=f(x)dxdA窄曲边梯形△A叫典型面积元素。于是Af(x)dx=dA可abx+dxb文A = lim Ef(x)dx = Jf(x)dx4169

169 2、以不变高代替变高，以矩形代替曲边梯形，给出“零”的近似值 Δ Δ Af x xxi n i ii i i i ≈ ∀∈ ( ) [ , ]( , , ) ξ ξ −1 = 1 2 " 3、积零为整，给出“整”的近似值 Af x i i i n ≈ ∑ = ( ) ξ Δ 1 4、取极限，使近似值向精确值转化 A f x f x dx i i i n a b = ∑ = ∫ → = lim ( ) ( ) λ ξ 0 1 Δ 上述做法蕴含有如下两个实质性的问题： (一)、若将[,] a b 分成部分区间[ , ]( , , ) xxi n i i −1 = 1 2 " ，则 A相应地分成部 分量ΔAi n i ( , , ) = 1 2 " ，而 A Ai i n = ∑ = Δ 1 这表明：所求量 A对于区间[,] a b 具有可加性。 (二)、用 f x i i ( ) ξ Δ 近似ΔAi，误差应是Δxi的高阶无穷小。 只有这样，和式 f x i i i n ( ) ξ Δ = ∑ 1 的极限方才是精确值 A。 故，确定 ( ) ( ( ) ( ) ) i i i i i i i ΔA ≈ f ξ Δx ΔA − f ξ Δx = o Δx 是关键

通过对求曲边梯形面积问题的回顾、分析、提炼，我们可以给出用定积分计算某个量的条件与步骤。二、元素法1、能用定积分计算的量U，应满足下列三个条件(1)、U与变量x的变化区间[a,b]有关；(2)、U对于区间[a,b]具有可加性；(3）、U部分量△U,可近似地表示成f（S）·△xi。2、写出计算U的定积分表达式步骤(1)、根据问题，选取一个变量x为积分变量，并确定它的变化区间[a,b]：(2)、设想将区间[a,b]分成若干小区间，取其中的任一小区间[x,x+dx]，求出它所对应的部分量△U的近似值△U~f(x)dx（f(x)为[a,b]上一连续函数)则称f(x)dx为量U的元素，且记作dU=f(x）dx。(3)、以U的元素dU作被积表达式，以[α,b]为积分区间，得bU = J f(x)dxa这个方法叫做元素法，其实质是找出U的元素dU的微分表达式dU=f(x)dx(a≤x≤b)因此，也称此法为微元法小结：本小结讲述了元素法（注意微元法的本质）作业：170

170 通过对求曲边梯形面积问题的回顾、分析、提炼， 我们可以给出用定积分 计算某个量的条件与步骤。 二、元素法 1、能用定积分计算的量U ，应满足下列三个条件 (1)、U 与变量 x 的变化区间[,] a b 有关； (2)、U 对于区间[,] a b 具有可加性； (3)、U 部分量ΔUi可近似地表示成 f x i i ( ) ξ ⋅ Δ 。 2、写出计算U 的定积分表达式步骤 (1)、根据问题，选取一个变量 x 为积分变量，并确定它的变化区间[,] a b ； (2)、设想将区间[,] a b 分成若干小区间，取其中的任一小区间[, ] x x + dx ， 求出它所对应的部分量ΔU 的近似值 ΔU ≈ f ( ) x dx ( f ( ) x 为[,] a b 上一连续函数) 则称 f ( ) x dx 为量U 的元素，且记作dU = f ( ) x dx 。 (3)、以U 的元素dU 作被积表达式，以[,] a b 为积分区间，得 U f x dx a b = ∫ ( ) 这个方法叫做元素法，其实质是找出U 的元素dU 的微分表达式 dU = ≤ f () ( ) x dx a x ≤ b 因此，也称此法为微元法。 小结：本小结讲述了元素法 （注意微元法的本质） 作业：

$6.2平面图形的面积教学目的：学会用元素法计算平面图形的面积教学重点：直角坐标系下平面图形的面积计算教学难点：面积元素的选取教学内容：一、直角坐标的情形由曲线y=f(x）（f(x)≥o）及直线x=a与x=b（a<b）与x轴所围成的曲边梯形面积A。yy=f(r)dAR0ax+dxbXbA=Jf(x)dx其中：f(x)dx为面积元素。a由曲线y=f(x）与y=g(x）及直线x=a，x=b（a<b)且f(x)≥g(x)所围成的图形面积A。A=J(αx)y= g(x)xDx+dxbA=j f(x)dx -jg(x)dx = j[ f(x)- g(x)jdx其中：[f(x)-g(x)]dx为面积元素。171

171 §6.2 平面图形的面积 教学目的：学会用元素法计算平面图形的面积 教学重点：直角坐标系下平面图形的面积计算 教学难点：面积元素的选取 教学内容： 一、直角坐标的情形 由曲线 y = ≥ f ( )( ( ) ) x f x 0 及直线 x = a 与 x = b ( a b < ) 与 x 轴所围成的曲边梯形面积 A。 A f x dx a b = ∫ ( ) 其中： f ( ) x dx 为面积元素。 由曲线 y = f ( ) x 与 y g = ( ) x 及直线 x = a ， x = b ( a b < )且 f () () x ≥ g x 所围成的图形面积 A。 = ∫ − ∫ = ∫ − b a b a b a A f ( x) dx g ( x) dx [ f ( x) g ( x) ] dx 其中：[ ( ) ( )] f x − g x dx 为面积元素

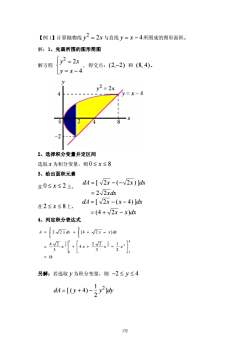
=2x与直线y=x-4所围成的图形面积。【例1】计算抛物线2解：1、先画所围的图形简图y2 = 2xy解方程得交点：(2,-2）和（8,4)。y=x-4yy2 = 2x47-x20748-22、选择积分变量并定区间选取x为积分变量，则0≤x≤83、给出面积元素dA=[V2x -(-~2x)]dx在0≤x≤2上,=2/2xdxdA =[ V2x -(x - 4) ]dx在2≤x≤8上,=(4 + /2x - x)dx4、列定积分表达式2xdx + j[4 +2x - x]dx4V2[4x+21.133= 18另解：若选取y为积分变量，则-2≤y≤41y? jadydA=[(y + 4)-1L172

172 【例 1】计算抛物线 y x 2 = 2 与直线 y = x − 4所围成的图形面积。 解：1、先画所围的图形简图 解方程 y x y x 2 2 4 = = − ⎧ ⎨ ⎩ , 得交点：(, ) 2 2− 和 (, ) 8 4 。 2、选择积分变量并定区间 选取 x 为积分变量，则0 8 ≤ ≤ x 3、给出面积元素 在0 2 ≤ ≤ x 上， dA x x dx xdx = −− = [ ( )] 2 2 2 2 在2 8 ≤ ≤ x 上， dA x x dx x x dx = −− =+ − [ ( )] ( ) 2 4 4 2 4、列定积分表达式 18 2 1 3 2 2 4 3 4 2 2 2 [ 4 2 ] 8 2 2 2 3 2 0 2 3 8 2 2 0 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = + + − = + + − ∫ ∫ x x x x A x dx x x dx 另解：若选取 y 为积分变量，则 −2 4 ≤ y ≤ dA y y dy = +− [( ) ] 4 1 2 2

412J( y+ 4A=)dyV2-2,3 /4y=+4V26-2= 18显然，解法二较简洁，这表明积分变量的选取有个合理性的问题。22=1所围成的面积（a>0,b>0）。【例2】求椭圆2+62a解：据椭圆图形的对称性，整个椭圆面积应为位于第一象限内面积的4倍。yV=b,h2x0xx+dx取x为积分变量，则0≤x≤a，y=bldA = ydx =dxORaa4[badx故A= 4J ydx:(*)O00元(0≤t≤作变量替换x=acost2bbsint,dx =-asintdt则y==2a173

173 A y y dy y y y = +− ∫ = +− = − − ( ) 4 1 2 2 4 6 1 8 2 4 2 2 3 2 4 显然，解法二较简洁，这表明积分变量的选取有个合理性的问题。 【例 2】求椭圆 x a y b 2 2 2 2 + = 1所围成的面积 ( ,) a b > > 0 0 。 解：据椭圆图形的对称性，整个椭圆面积应为位于第一象限内面积的 4 倍。 取 x 为积分变量，则 0 ≤ ≤ x a ， y b x a = −1 2 2 dA ydx b x a ==−1 dx 2 2 故 A ydx b x a dx a a = 4 41 ∫ = − ∫ 0 2 2 0 ( * ) 作变量替换 x a = cost ( ) 0 2 ≤ ≤t π 则 y b x a = −= 1 b t 2 2 sin ， dx a td = − sin t

0(**)A = 4J(bsint)(-asint)dt元2K12=4abj sin dt =4ab.-1= maob22!!0例：从抛物线y=x2-1上的点P引抛物线y=x的切线，证明该切线与y=x?所围成的面积与P点的位置无关解：设Q(x,),Q(x2,y2）分别表示从点P(xo,%)向抛物线y=x2引出的两条切线的切点.y=x2在点9(x,J）的切线方程y-y=2x(x-x)即y-x =2x(x-x)又= x -1= x =x +1,x = x -1于是切线PQ,PQ,的方程分别为y = 2(x + 1)x-(x +1)y= 2(x -1)x-(x。 -1)2由y=x,P9,及PQ,所围图形的面积为A = [ [x - 2(x0 -1)x+(x -1)]dx+[* [x? -2(xo +1)x+(x +1)"]dx 可见A与x无关，A与点P(x%）位置无关x21与直线x=-V3，x=V3围成的图形面积例：求曲线y=2J1+xy解：两曲线交点为(1,).由于图形关于y轴对称1V5x2x).dx+故A：:d1+x21+.3n174

174 A b t a t dt = − 4 ∫ 2 0 ( sin )( sin ) π ( * * ) ab tdt ab πab π π ⋅ = − = = ⋅ ∫ 2!! 2 (2 1)!! 4 sin 4 2 0 2 例： 2 2 从抛物线 上的点 引抛物线 的 y =− = x P yx 1 2 切线 证明该切线与 所围成 , y x = 的面积与 点的 P 位置无关. 解：设 111 2 2 2 Qxy Qx y ( , ), ( , ) 分别表示从点 0 0 Px y (, )向抛物线 2 y = x 引出的两条切线 的切点. 2 y = x 在点 111 Qxy (, )的切线方程: 11 1 y −= − y xx x 2( ) 即 2 0 1 10 1 y x xx x −= − 2( ) 又 2 00 10 10 yx xx xx = −⇒ = + = − 1 1, 1 于是切线 1 2 PQ PQ , 的方程分别为 2 0 0 y x xx = +−+ 2( 1) ( 1) 2 0 0 y x xx = −−− 2( 1) ( 1) 2 1 2 由 及 y x PQ PQ = , 所围图形的面积为 0 0 0 0 1 2 22 2 00 00 1 [ 2( 1) ( 1) ]d [ 2( 1) ( 1) ]d x x x x A x x xx x x x xx x + − = − −+− + − +++ ∫ ∫ 2 . 3 = 可见 A x 与 无关 0 , 0 0 A Px y 与点 (, ) 位置无关 例： 2 2 1 , 3, 2 1 x yy x x = = =− + 求曲线 与直线 x = 3 . 围成的图形面积 解：两曲线交点为 1 1 (1, ),( 1, ). 2 2 − 由于图形关于 y 轴对称, 故 2 2 1 3 2 2 0 1 1 1 2 ( )d 2 ( )d 1 2 21 x x Ax x x x = − ⋅+ − ⋅ + + ∫ ∫ − 3 3 O x y 2 1 1 y x = + 2 2 x y = − 1 1 1

2+V333例：求介于直线x=0.x=2元之间由曲线y=sinx和y=cosx所围成的平面图形的面积解：画草图，两曲线的交点yt=sin(),V25y=cosx4GT4*ny=cosx5元2 (sin x-cos x) dx|= [(cosx-sin x)dx1=4元02元[ (sinx-cos x)dx+J(cosx-sin x)dx=4/24y=sinx例：求双纽线r?=αcos20所围平面图形的面积解：由对称性知总面积=4倍第一象限部分面积A=4A,a?cos20de=a?4=4L例计算由曲线(x2+）=α(x2-)所围成的区域在圆x2+α"的外面部分的面积2解：曲线(x+y2）=α(x2-y）是双纽线方程极坐标方程：r2=αcos21α极坐标方程：r=圆x+=CV2V交点由对称性0=2hacos20-d=a1=4.aOJ6175

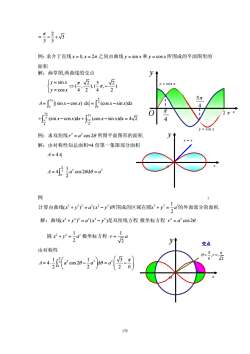
175 2 3 3 3 π = −+ 例：求介于直线 x x = 0, 2 = π 之间由曲线 y = sin x 和 y = cos x所围成的平面图形的 面积 解：画草图,两曲线的交点 sin 25 2 ( , ), ( , ) cos 42 4 2 y x y x π π ⎧ = ⎨ ⇒ − ⎩ = 2 4 0 0 A x x x x xx (sin cos ) d (cos sin )d π π = − =− ∫ ∫ 5 2 4 5 4 4 (sin cos )d (cos sin )d 4 2 x xx x xx π π + −+ −= ∫ ∫ π π 例：求双纽线 2 2 r a = cos 2θ 所围平面图形的面积. 解：由对称性知总面积=4 倍第一象限部分面积 1 A A = 4 2 2 4 0 1 4 cos 2 d . 2 Aa a π = = θ θ ∫ 例 ： 2 22 2 2 2 2 2 2 1 ( )( ) . 2 计算由曲线 所围成的区域在圆 的外面部分的面积 x y ax y x y a + = − += 解： 2 22 2 2 2 曲线 是双纽线方程 ( )( ) . x y ax y += − 2 2 极坐标方程: cos 2 . r a = θ 22 2 1 2 圆 x + = y a 1 : 2 极坐标方程 r a = 由对称性 2 22 6 0 1 13 4 cos 2 d 2 2 26 A a aa π π θ θ ⎛ ⎞ ⎛ ⎞ =⋅ − = − ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ∫ y x = cos y x = sin O x y 2 π 4 π 5 4 π y x = O x y , 6 2 a r π θ = = 交点 O x y

例：求界于二椭圆+xy2=1(a>b>0)之间图形面积=1b?b2aa'12x2解：所求面积A为在第一象限中由直线V=x,x轴及椭圆q2b2y所围图形面积的8倍x2y22x2=+b2将椭圆=1化为极坐标方程ab2Q2y=Xy2x=rcoso代入椭圆26y=rsingaxa’b2得2=4r2(0)d0,A=8.Va”cos?+b’sin?g2J0y=x1[3r(0)d = 4a2b [A=8.dea?cos?+b?sin?16d= 4ab-tanの)ab2b2acos e(1+tantan?0)1+aab=4abarctan(a极坐标情形二、设平面图形是由曲线r=β()及射线=α，=β所围成的曲边扇形。β0+doAA=r()d75取极角θ为积分变量，则α≤θ≤β,在平面图形中任意截取一典型的面积元素△A，它是极角变化区间为[0,0+dO]的窄曲边扇形。△A的面积可近似地用半径为r=(の)，中心角为dO的窄圆边扇形的面积来代替，即176

176 例： 22 22 22 22 1, 1( 0) xy xy a b ab ba 求界于二椭圆 之间图形面积 + = + = >> . 解：所求面积 A 为在第一象限中由直线 y x = , x 轴及椭圆 2 2 2 2 1 x y b a + = 所围图形面积的 8 倍. 将椭圆 2 2 2 2 1 x y b a + = 化为极坐标方程. 将 cos sin x r y r θ θ ⎧ = ⎨ ⎩ = 代入椭圆 2 2 2 2 1, x y b a + = 得 2 2 2 2 4 2 2 22 0 1 , 8 ( )d cos sin 2 a b r Ar a b π θ θ θ θ = =⋅ + ∫ 2 22 4 4 2 2 22 0 0 1 1 8 ( )d 4 d 2 cos sin A r ab a b π π θ θ θ θ θ =⋅ = + ∫ ∫ 2 4 2 0 2 2 2 1 4 d cos (1 tan ) b b a π θ θ θ = + ∫ 4 2 0 2 2 1 4 ( tan ) 1 tan b ab d b a a π θ θ = + ∫ 4 arctan( ) b ab a = 二、 极坐标情形 设平面图形是由曲线 r = ϕ( ) θ 及射线θ = α ，θ = β 所围成的曲边扇形。 取极角θ 为积分变量，则 α ≤ θ ≤ β ,在平面图形中任意截取一典型的面积元 素ΔA，它是极角变化区间为[, ] θ θ + dθ 的窄曲边扇形。 ΔA的面积可近似地用半径为r = ϕ( ) θ ， 中心角为dθ 的窄圆边扇形的面积来 代替，即 y = x y = −x 2 2 2 2 1 x y a b + = 2 2 2 2 1 x y b a + = x y O

A~deLoe[p(の)Pd从而得到了曲边梯形的面积元素dA=β1p(0)d0从而A=【例3】计算心脏线r=a(1+cos①）（a>O)所围成的图形面积。解：由于心脏线关于极轴对称，9021201.560150C1802103024030027020元12元1a?(1+cos0)2d0= a022cos2A=2Ide20200元122元408a2AO-de= 4a~Jcos4tdt「cos=t22003= 8a2 (4 - 1)!元.2一-a元224!!小结求在直角坐标系下、极坐标系下平面图形的面积。作业177

177 ΔA d ≈ 1 2 2 [ ( )] ϕθ θ 从而得到了曲边梯形的面积元素 dA d = 1 2 2 [ ( )] ϕθ θ 从而 A d = ∫ 1 2 2 ϕθθ α β ( ) 【例 3】计算心脏线r =+ > a a ( cos ) ( ) 1 0 θ 所围成的图形面积。 解： 由于心脏线关于极轴对称， A a da d a d a tdt a a t = + ∫ = ⎛ ⎝ ⎜ ⎞ ⎠ ∫ ⎟ = ∫ ∫ = − ⋅ = = 2 1 2 1 2 2 4 2 8 8 4 1 4 2 3 2 2 2 0 2 2 0 2 2 4 0 2 2 4 0 2 2 2 ( cos ) cos cos cos ( )!! !! θ θ θ θ θ θ π π π π π θ π 令 小结 求在直角坐标系下、极坐标系下平面图形的面积. 作业