《高等数学》课程教学资源（PPT课件）第二章 导数与微分 2-05 第五节 函数的微分

第五节函数的微分■微分的定义微分的几何意义1微分公式与运算法则小结思考题

第五节 函数的微分 ◼ 微分的定义 ◼ 微分的几何意义 ◼ 微分公式与运算法则 ◼ 小结 思考题

导数——表示函数在一点处由自变量所引起的函数变化的快慢程度微分——是函数在一点处由于自变量微小变化所引起的改变量的近似值导数与微分个有着密切的联系

导数 微分 导数与微分 表示函数在一点处由自变量所引起 的函数变化的快慢程度. 是函数在一点处由于自变量微小变化 所引起的改变量的近似值. 有着密切的联系

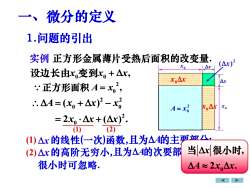
微分的定义一、1.问题的引出实例正方形金属薄片受热后面积的改变量(Ar)XoAx设边长由x.变到x。+△x，LoAxAr：正方形面积 A=x,.. A = (x, + Ax)° - x)XAxxeA=xi= 2x, · Ax + (△x)?(1)(2)要公(1)△x的线性(一次)函数,且为△A的主1当Ax很小时，(2)△x的高阶无穷小,且为△A的次要部很小时可忽略AA~2x.Ar

正方形金属薄片受热后面积的改变量. 2 0 A = x x0 0 x 0 0 设边长由x x x 变到 +  , 2 0 正方形面积 A x = , 2 2 0 0  = +  − A x x x ( ) 2 0 =   +  2 ( ) . x x x (1) (2) 且为A的主要部分; x (1) (2) x x 2 (x) 1.问题的引出 实例 x x x 0 x x 0 一、微分的定义 的线性(一次)函数, 且为A的次要部分,当x 很小时可忽略. 0 , 2 . x A x x     的高阶无穷小, 当 很小时

再如，设函数y=x3在点x,处的改变量为△x时求函数的改变量△yAy =(xo + Ax) - xi3x) . Ax/+ 3x, :(Ax)? +(Ax)3.(1)(2)当△x很小时,(2)是△x的高阶无穷小o(△x),:. 4y ~ 3xi : 4x.既容易计算文是较好的近似值

再如, 3 0 设函数 y x x x =  在点 处的改变量为 时, 3 0 3 0 y = (x + x) − x 3 3 ( ) ( ) . 2 3 0 2 = x0  x + x  x + x (1) (2) 当 x 很小时,  y  (2) ( ), 是  x o x 的高阶无穷小 既容易计算又是较好的近似值 求函数的改变量y. 3 . 2 0 x  x

对一般函数y= f(x),如果y= f(x)满足一定条件，则函数的增量4可以表示为Ay = A△x + o(△x)其中A是不依赖于△r的常数，因此A△r是A的线性函数，且它与△V之差Ay - AAx =0(△x)Ax ~ △y当A￥0,且△x很小时对一般函数y=f(x),如果存在这样的近似公式，则无论在理论分析上还是在实际应用中都是十分重要的

对一般函数y f x = ( ), 其中A x 是不依赖于 的常数, y = Ax 当A  0, Ax  y 如果y f x = ( )满足 一定条件, y 因此A x x   是 的 线性函数, 且它与y之差 对一般函数 则无论在理论分析上还是在实际 + o(x). 则函数的增量 可以表示为 如果存在这样的 近似公式, 应用中都是十分重要的. o(x) 且 x 很小时, y = f (x), y − Ax =

2.微分的定义定义设函数y= f(x)在某区间内有定义x,及x,+△xr在这区间内如果A为微分系数A△x + o(Ax)Ay = f(xo + △x)- f(xo) =成立(其中A是与△x无关的常数,则称函数y=f(x)在点x,可微，并称A·△x为函数y=f(x)在点x,相应于自变量增量△x的微分，记作dy|x=x,或df(xo),即dy| =x, = A·Ax

2. 微分的定义 定义 设函数y = f (x)在某区间内有定义, , x0 及 x0 + x在这区间内 y = f (x0 + x) − f (x0 ) = 如果 成立(其中A是与x无关的常数), 0 y = f (x)在点x 则称函数 A x 0 d x x y = y = f (x)在点x0相应于自变量 d . 0 y A x 即 x= x =   可微, d ( ), x0 或 f 微分, 记作 并称 为函数 增量x的 A为微分系数 Ax + o(x)

满足什么条件的函数是可微的呢？3.微分的系数A如何确定呢？定在x)微分与导数有何关系呢？下面的定理回答了这些问题dy=f'(x)Ax证(1)必要性：f(x)在点x,可微:. Ay = A . △x + o(△x),Ayo(△x:. lim4limA+ArAr-→0 LAxAr→0即函数f(x)在点x,可导,且A= f'(x)

3. 可微的充分必要条件 定理 函数 f (x)在点x0 可微 证 (1) 必要性 ( ) ,  f x 在点x0可微 y = A x + o(x),  = A. ( ) , 即函数 f x 在点x0 可导 函数 f (x) d ( ) . y = f  x0 x 即有 ( ). x0 且A = f   , 在点x0处可导 ( ), 0 且 A = f  x =   x y x o x A   + ( ) 0 lim x→   0 lim x→ 满足什么条件的函数是可微的呢？ 微分的系数A如何确定呢? 微分与导数有何关系呢? 下面的定理回答了这些问题

定理函数f(x)在点x,可微台/函数f(x)在点x处可导,且A=f(x),即有dy=f(x)△x(2)充分性:函数f(x)在点x,可导AyAy= f'(x),:. Jim即= f'(x,)+α,Ar-→>0 △xAr(r →0, α→0)从而 4y = f'(x)· 4x +α· (4x)= f'(x). Axr + o(Ax),:函数f(x)在点x,可微,且f(xo)= A.:.可导台可微.其微分一定是dy =f(x)x求导法又叫微分法

(2) 充分性 ( ) ( ), y = f  x0  x +  x ( ) , =  0 +    f x x y 即 ( ) , 函数f x 在点x0可导 lim ( ), 0 0 f x x y x =      → ( ) ( ), = f  x0  x + o x ( ) , 函数 f x 在点x0可微 可导 可微. 求导法又叫微分法 d ( ) . 0 y = f  x x 从而 ( ) . 且 f  x0 = A  其微分一定是 定理 函数 f (x)在点x0 可微 函数 f (x) 即有  , 在点x0处可导 ( ), 0 且 A = f  x d ( ) . y = f  x0 x (x →0, →0)

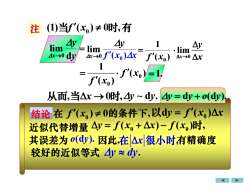
注(1)当f(x)≠0时,有y4y7Aylimlimlim4x=0 f'(xo)4x4x-→0dyf'(xo)Ar→0 Ax1=1(xof'(xo)从而,当△x 一→0时,4y ～ dy.Ay = dy + o(dy)结论在f（x）±0的条件下，以dy=f（x）A近似代替增量 Ay= f(x。+△r)-f(x,)时,其误差为o(dy).因此在△x很小时有精确度较好的近似等式4y～dy

注 = → y y x d lim 0   ( ) 1 x0 f  = 0 (1) ( ) 0 , 当f x   时 有   = ( ) 1 x0 f 从而, 0 , 当 →x 时 即dy y 是 的 ( 0). 当 →x 微分的实质 y x   0 lim → ( ) x0 f  = 1. y = dy + o(dy). d ( )0 又由于 y f x x x =    是 的 y ~ dy. 线性函数, 线性主部. f ( x )x 0  0 lim x y  → x    主部, 称dy y 是 的 所以在 条件下, 0 f x ( ) 0  在 的条件下, d ( )0 以 y f x x =   0 0 近似代替增量  = +  − y f x x f x ( ) ( ) , 时 其误差为 o(dy). 因此, 在 x 很小时, 有精确度 较好的近似等式 y  dy. 结论 0 f x ( ) 0 

注(2)函数y=f(x)在任意点x处的微分，称为函数的微分，记作dy 或 df(x),即dy = f'(x)4x与x和4x有关(3)通常把自变量x的增量4x称为自变量的微分，记作dx，即dx=4x.dy:. dy = f'(x)dx→f'(x)dx导数又称为微商

与x和x有关 (3)通常把自变量x的增量x dy = f (x)dx ( ) d d f x x y =  导数又称为微商 称为函数 的微分, 记作dy 或 df (x)， 即dy = f (x)x. 称为自变量的 微分,记作 dx, 即dx = x. 注 （2）函数y =f (x)在任意点x处的微分