《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用 3-习题课

第三章微分中值定理与导数的应用习题课>教学要求>典型例题

第三章 微分中值定理与导数的应用 ➢教学要求 ➢典型例题 习 题 课

一、教学要求1：理解罗尔(Rolle)定理和拉格朗日(Lagrange定理2.了解柯西(Cauchy)定理和泰勒(Tayloy)定理3．理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法

1. 理解罗尔(Rolle) 定理和拉格朗日(Lagrange) 定理. 2. 了解柯西(Cauchy)定理和泰勒(Tayloy)定理. 3. 理解函数的极值概念,掌握用导数判断函数 的单调性和求极值的方法. 一、教学要求

4.会用导数判断函数图形的凹凸性，会求拐点，会描绘函数的图形（包括水平，铅直和斜渐近线）.会求解最大值和最小值的应用问题5.会用洛必达(L,Hospital)法则求不定式的极限6.了解曲率和曲率半径的概念并会计算曲率和曲率半径

4. 会用导数判断函数图形的凹凸性,会求拐点,会描 绘函数的图形(包括水平,铅直和斜渐近线).会求 解最大值和最小值的应用问题. 5. 会用洛必达(L,Hospital)法则求不定式的极限. 6. 了解曲率和曲率半径的概念并会计算曲率和曲 率半径

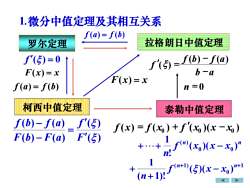
1.微分中值定理及其相互关系f(a) = f(b)拉格朗日中值定理罗尔定理F(5) =f(b)-f(α)f()=0b-aF(x)= xF(x)= xn=0f(a) = f(b)柯西中值定理泰勒中值定理f(b)-f(a) - f(E)f(x) = f(xo) + f(x)(x -xo)F(b)-F(a)F'()f(n)(x,)(x -xo)"(5)(x -xo)"+1n+

f (a) = f (b) 1.微分中值定理及其相互关系 罗尔定理 f ( ) = 0 ( ) ( ) ( ) ( ) ( ) ( )   F f F b F a f b f a   = − − 拉格朗日中值定理 ( ) ( ) ( ) f a f b F x x = = 柯西中值定理 F(x) = x 泰勒中值定理 1 0 ( 1) ( )( ) ( 1)! 1 + + − + + n n f x x n  n n f x x x n ( )( ) ! 1 0 0 ( ) ++ − ( ) ( ) ( )( ) 0 x0 x x0 f x = f x + f  − b a f b f a f − −  = ( ) ( ) () n = 0

2.微分中值定理的主要应用(1）研究函数或导数的性态(2)证明方程根的存在性(3）证明恒等式或不等式(4)证明有关中值问题的结论

2. 微分中值定理的主要应用 (1) 研究函数或导数的性态 (3) 证明恒等式或不等式 (4) 证明有关中值问题的结论 (2) 证明方程根的存在性

3.有关中值问题的解题方法利用逆向思维，设辅助函数.一般解题方法：(1)证明含一个中值的等式或根的存在,多用罗尔定理,可用原函数法找辅助函数(2)若结论中涉及到含中值的两个不同函数,可考虑用柯西中值定理(3)若结论中含两个或两个以上的中值,必须多次应用中值定理(4)若已知条件中含高阶导数,多考虑用泰勒公式有时也可考虑对导数用中值定理

利用 一般解题方法: 证明含一个中值的等式或根的存在, 若结论中涉及到含中值的两个不同函数,可考虑用 若已知条件中含高阶导数, 若结论中含两个或两个以上的中值, 3.有关中值问题的解题方法 (1) 可用原函数法找辅助函数. (2) 柯西中值定理. 中值定理. (3) (4) 有时也可考虑 多考虑用泰勒公式, 逆向思维,设辅助函数. 多用罗尔定理, 必须多次应用 对导数用中值定理

4.导数应用(1)）研究函数的性态：增减，极值，凹凸,拐点，渐近线，曲率(2）解决最值问题·目标函数的建立·最值的判别问题(③)其他应用：求不定式极限；几何应用相关变化率；证明不等式；研究方程实根等

(1) 研究函数的性态: 增减, 极值,凹凸,拐点,渐近线,曲率 (2) 解决最值问题 • 目标函数的建立 • 最值的判别问题 (3)其他应用: 求不定式极限;几何应用; 相关变化率; 证明不等式;研究方程实根等. 4.导数应用

二、典型例题f'(x)/≤M例1 f(x)在(a,b)内可导,且证明,f(x)在(a,b)内有界。证 取点xE(a,b),再取异于x的点xE(a,b),f(x)在以xo,x为端点的区间上用拉氏定理f(x)-f(x)= f()(x-x) (介于x,与x之间)f(x)=f(xo)+ f'(5)(x-xo)≤f(x)+f()x-xo定数≤f(xo)+M(b-a)=[K对任意xE(a,b),f(x)≤K，即证

二、典型例题 在 内可导,且 证明 在 内有界. 证 ( , ), 0 x  a b 再取异于 0 x 的点 x (a,b), 在以 x , x 0 为端点的区间上用 ( ) ( ) ( )( ) 0 0 f x − f x = f   x − x ( ) 介于x0与x之间  ( ) ( ) 0 f x + M b − a = K 定数 对任意 x (a,b), f (x)  K , 即证. 例1 取点 拉氏定理, ( ) ( ) ( )( ) 0 0 f x = f x + f   x − x 0 0 f (x ) + f ( ) x − x 

例2f(x)在[0,1]上连续,在 (0,1)内可导,且 f(1)=0证明至少存在一点 E(0,1),使2 f(5)f'()=&S间题转化为证 f()+2f()=0分析x=§ = 0xf (x)证 设辅助函数 F(x)=x2f(x)F(x)在[0,1]上用罗尔定理,三 E(0,1),使F()=25f()+f'()=02f(3)即有f'()=&S

在 内可导,且 证明至少存在一点 使 上连续,在 问题转化为证 设辅助函数 ( ) ( ) 2 F x = x f x F(x) 用罗尔定理,  (0,1) , 使 即有 例2 证 在[0,1]上 分析 ( ) = 0 2 x f x =  x [ ]  f () + 2 f () = 0 ( ) 2 ( ) ( ) 0 2 F   =  f  +  f   =

f(x)在[a,b]上连续,在(a,b)内可导,且例30<a<b,试证存在,nE(a,b),使a+bf'()=f'(n).2nf'()f'(n)f'()(b-a)f'(n)证欲证即要证b?-a?2na+b2nf(x)在[a,b]上用拉氏定理,故有(1)f(b)- f(a) = f'()(b-a),,E(a,b)又f(x)及x在[a,b]上用柯西定理,故有f'(n)f(b)- f(a) _f'(x)ne(a,b) (2)2 nb? -a?(x)x=na+b将(1)代入(2),化简得f()=f'(n), 5,ne(a,b).2n

在 内可导,且 试证存在 ( ). 2 ( )    f a b f  +  = 使 例3 上连续,在 欲证 , 2 ( ) ( )   f  a b f  = +  f (x)在[ a , b ]上用 故有 f (b) − f (a) = f ( )(b − a), 即要证 . 2 ( ) ( )  f  f   =  证 (b − a) 2 2 b − a  (a , b) 又 f ( x )及 2 x 在[ a , b ]上用 = − − 2 2 ( ) ( ) b a f b f a 将(1)代入(2),化简得 故有  , (a,b). 拉氏定理, 柯西定理, ( ), 2 ( )    f a b f  +  = ,  (a , b) 2 ( )  f   = f (x) ( ) 2 x  x = (1) (2)