《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用 3-05 第五节 函数的极值与最大值最小值

第五节函数的极值与最大值最小值函数的极值及其求法映射1最大值最小值问题■小结思考题

第五节 函数的极值与最大值最小值 ◼ 函数的极值及其求法映射 ◼ 最大值最小值问题 ◼ 小结 思考题

一、函数的极值及其求法1.函数极值的定义定义 若在x,的某邻域内恒有f(x) f(x)则称f(x)为函数f(x)的一个极大值(或极小值)函数的极大值与极小值统称为极值使函数取得极值的点xo(自变量）称为极值点

定义 , 若在x0 的某邻域内( ( ) ( )), 0 或f x  f x 则称f (x0 )为函数f (x)的一个 ( ) ( ) 0 f x  f x 极大值 (或极小值), 函数的极大值与极小值统称为极值. 极值点. 恒有 一、函数的极值及其求法 使函数取得极值的点x0 (自变量)称为 1. 函数极值的定义

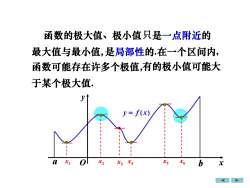
函数的极大值、极小值只是一点附近的最大值与最小值，是局部性的.在一个区间内，函数可能存在许多个极值,有的极小值可能大于某个极大值Vy= f(x)O1XsaX2X6bxiX3Xx

x1 x2 x3 x4 x5 x6 函数的极大值、极小值 是局部性的.在一个区间内, 函数可能存在许多个极值, 最大值与最小值, 有的极小值可能大 于某个极大值. 只是一点附近的 • • • • x y a O b y = f (x) • •

使导数f'(x)为零的点2.极值的必要条件叫做函数f(x)的驻点费马引理如果函数 f(x)在x处可导且f(x)在x.处取得极值,那么f(x)=0.定理1(必要条件)如果函数f(x)在点x,处取得极值,且在x处可导,则必有f'(x)=0.注(1)可导函数的极值点必是驻点，但函数的y=x3驻点却不一定是极值点V如,y=x,x=o = 0,x但x=0不是极值点

定理1(必要条件) 注 如, , 3 y = x 0, y x=0 = 但x = 0不是极值点. (1) 如果函数f (x)在点x0处取得 , 且在x0处可导 ( ) ( ) f x f x 使导数  为零的点 叫做函数 的 驻点. 可导函数的极值点 驻点却不一定是极值点. 必是驻点, 但函数的 那么 ( ) 0. 极值, 则必有f  x0 = 3 y = x x y O • 费马引理 如果函数 f (x)在x0处 可导, 0 且f (x)在x 处取得极值, ( ) 0. 0 f  x = 2. 极值的必要条件

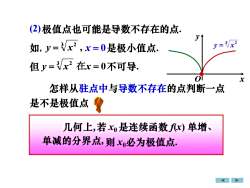
(2)极值点也可能是导数不存在的点Vy=/x?如，=x2，x=0是极小值点.但=x2在x=0不可导Ox怎样从驻点中与导数不存在的点判断一点是不是极值点几何上,若xo是连续函数f(x)单增、单减的分界点，则xo必为极值点

x y O 3 2 y = x 极值点也可能是导数不存在的点. 如, , 3 2 y = x 3 2 但 y = x 怎样从驻点中与导数不存在的点判断一点 单减的分界点, (2) 不可导. x = 0 是极小值点. 是不是极值点 若 x0 是连续函数 f(x) 单增、 则 x0必为极值点. 几何上, • 在x = 0

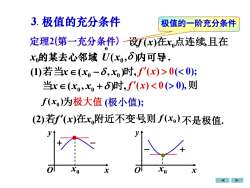
3.极值的充分条件极值的一阶充分条件定理2(第一充分条件）一设f(x)在x点连续,且在xo的某去心邻域 U(xo,)内可导。(1)若当x E(x -S,x)时,f'(x)>0(0),则f(x,)为极大值 (极小值);(2)若f(x)在x,附近不变号则 f(x)不是极值,y2totXoXoxx

定理2(第一充分条件) 设f (x)在x0 点连续,且在 (1) ( , ) , 若当x x0 − x0 时 f (x)  0( 0); ( , ) , 当x x0 x0 + 时 f (x)  0 ( 0), 则 ( ) x0 f 为极大值 (2) ( ) , 若f  x 在x0 附近不变号 ( ) x0 则 f 不是极值. (极小值); 极值的一阶充分条件 x y O x0 • + − x y O x0 − + • ( , ) . 0 o x0的某去心邻域 U x  内可导 3. 极值的充分条件

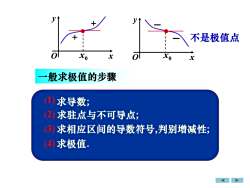
不是极值点olotXoXoxx般求极值的步骤(1)求导数;2）求驻点与不可导点；③）求相应区间的导数符号，判别增减性：(4)求极值

x0 x0 + − − + 一般求极值的步骤 求导数; 求驻点与不可导点; 求相应区间的导数符号,判别增减性; 求极值. (1) (2) (3) (4) 不是极值点 • • x y O x y O

2例1求 f(x)=(x+1)(x-1)3 的极值及单调区间解 (1) f'(x)=3(x+1)(x-1)3 +=(x+1)(x-1)3(x +1)(11x - 7)3(x-1)37(2)驻点:x =-1,x=导数不存在的点：x=1.11(3)列表:求相应区间的导数符号,判别增减性确定极值点和极值

例1 解 ( ) ( 1) ( 1) . 3 2 求 f x = x + 3 x − 的极值及单调区间 3 2 2 f (x) = 3(x + 1) (x −1) 3 1 3 ( 1) ( 1) 3 2 − + x + x − 3 1 2 3( 1) ( 1) (11 7) − + − = x x x (1) (2)驻点: x = −1, 导数不存在的点: . 11 7 x = x = 1. (3)列表:求相应区间的导数符号,判别增减性, 确定极值点和极值

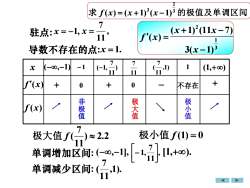
求 f(x)=(x+1)(x-1)3 的极值及单调区间7(x +1)°(11x - 7)驻点:x=-1,x=11f'(x) =3(x -1)3导数不存在的点：x=11(-11)1-1()x(-00,-1)(1,+8)1i+f(x)00++不存在非极值极小值极大值f(x)极小值f(1)=0极大值f(~2.2单调增加区间:(-0,-11,[-1,引], [1,+),单调减少区间：,1)一

x f (x) f (x) − 1 ) (1,+) 11 7 (−1, 11 7 ,1) 11 7 (−,−1) ( 1 + 0 − 非 极 值 极 小 值 ) 2.2 极小值 f (1) = 0 11 7 极大值 f (  + 0 不存在 + 极 大 值 驻点: x = −1, 导数不存在的点: , 11 7 x = x = 1. ( ) ( 1) ( 1) . 3 2 求 f x = x + 3 x − 的极值及单调区间 f (x) = 3 1 2 3( 1) ( 1) (11 7) − + − x x x 单调增加区间: , [1,+). 11 7 1,       (−,−1], − 单调减少区间: ,1). 11 7 (

证对于驻点，有时还可以利用函数在该点寸处的一阶导数的正负号来判断极值点f'(x)- f'(x)f'(x)证 f"(x)= lim 0;当x >xo,f'(x)<0.第一充分条件x.处取极大值自己已证极小值情形

定理3(第二充分条件) 证 ( ) 0, 如果 f  x0 = 极大值 (极小值). f (x0 )  0 ( 0),则f (x0 )为 极值的二阶充分条件 f (x0 ) =  0, 0 0 ( ) ( ) lim 0 x x f x f x x x −  −  → 0 ( ) lim 0 x x f x x x −  = → 因此,当 | | x − x0 充分小时,由极限的保号性 0. ( ) 0  −  x x f x 可见, f ( x) 与 x − x0 异号. , 当x  x0 f (x)  0; , 当x  x0 f (x)  0. 所以, ( ) . 第一充分条件 f x 在点x0 处取极大值 对于驻点,有时还可以利用函数在该点 处的二阶导数的正负号来判断极值点. 自己证极小值情形