《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用 3-02 第二节 洛必达法则

洛必达（LHospital）法国数学家1661-1705)第二节洛必达法则08型,型未定式080.80,80一80型未定式0°,1°,80°型未定式小结 思考题

小结 思考题 0,−型未定式 0 0 ,1  , 0 型未定式 第二节 洛必达法则 洛必达 (L‘Hospital) 法国数学家(1661-1705) 型 型未定式   , 0 0 ◼ ◼ ◼ ◼

定义如果当x→a(或x→8)时,两个函数f(x)与F(x)都趋于零或趋于无穷大,那末极限0f(x)8称为=lim或一型未定式。F(x)0x-→a8(x-→0)In sin axtan xlim如,limx->0 In sin bxx-→0x未定意味着关于它的极限不能确定出一般的结论，而并不是在确定的情况下关于它的极限不能确定在第一章中看到，两个无穷小之商或两个无穷大之商,其极限都不能直接利用极限运算法则来求

如果当x → a(或x → )时, 其极限都不能直接利用极限运算 在第一章中看到, 无穷大之商, 法则来求. 称为 ( ) ( ) lim ( ) F x f x x x a → → 那末极限 定义 0 0   或 型未定式. 如, x x x tan lim →0 bx ax x lnsin lnsin lim →0 ) 0 0 ( ( )   未定 意味着关于它的极限不能确定出一般的 不能确定. 结论, 而并不是在确定的情况下关于它的极限 两个无穷小之商或两个 两个函数 f (x)与F(x)都趋于零或趋于无穷大

这一节介绍一个求未定式极限的有效方法f(x)此方法的关键是将lim的计算问题转化为F(x)x-→a(x-→0)f'(x)lim的计算.其基本思想是由微积分著名F'(x)x→a(x-→00)先驱，17世纪的法国数学家洛必达(LHospital)提出的,后人对他的思想作了推广,从而产生了简便而重要的洛必达法则

这一节介绍一个求未定式极限的有效方法, 此方法的关键是将 ( ) ( ) lim ( ) F x f x x x a → → 的计算问题转化为 ( ) ( ) lim ( ) F x f x x x a   → → 的计算. 其基本思想是由微积分著名 先驱, 从而产生了简 洛必达法则. 提出的,后人对他的思想作了推广, 17世纪的法国数学家洛必达(L‘Hospital) 便而重要的

08型,二型未定式08定理1设函数f(x)及F(x)满足条件(1)lim f(x) = 0(或o0), lim F(x) = 0(或0);x→a(2) f(x),F(x)在点a的邻域内可导(点a处可除外)且 F'(x)±0;f(x)= A(或);(3) limF'(x)x-→af(x)f(x)= A(或).则: limlimx-a F'(x)F(x)x-→a

定理1 设函数 f (x)及F(x)满足条件 一、 型 型未定式   , 0 0 ( ); ( ) ( ) (3) lim =    → A 或 F x f x x a (2) f (x),F(x)在点a的邻域内可导,(点a 处 (1)lim ( ) = 0( ), → f x 或 x a lim ( ) = 0( ); → F x 或 x a 可除外)且 F(x)  0; = → ( ) ( ) lim F x f x x a 则 ( ). ( ) ( ) lim =    → A 或 F x f x x a

(1)lim f(x) = 0, lim F(x) = 00证（仅对一型型给出证明0若f(x),F(x)在点a连续,则由条件(1)必有 f(a)= F(a)= 0.若f(x),F(x)在点a不连续由于lim f(x)=0,xalim F(x)= 0,可补充定义 f(a)= F(a)= 0.→-使f(x),F(x)在x=a点连续任取点x,a-sa)f(x),F(x)满足1)在[a,x]上连续;2)在(a,x)内可导,且F(x)± 0.①)直泌(型在点4的邻域内可导(点β处除外)

证 若f (x),F(x)在点a连续, f (a) = F(a) = 0. (1)lim ( ) = 0, → f x x a lim ( ) = 0; → F x x a 则由条件(1), 必有 若f (x),F(x)在点a不连续, lim ( ) = 0, → F x x a f (a) = F(a) = 0. 使f (x),F(x)在x = a点连续. lim ( ) = 0, → f x x a 由 于 可补充定义 任取点x, a −  x  a + (不妨设x  a). ) 0 0 (仅对 型给出证明 f (x),F(x)满足 2)在(a, x)内可导,且F(x)  0. 且 F(x)  0; 1)在[a, x]上连续; (2) f ( x),F( x)在点a 的邻域内可导(点 a 处除外)

在(a,x)内至少存在点,使柯西定理f(x) - f(a)(在x与a之间)F(x)- F(a)Af'(x)当x→a时,→a,(3) limF'(x)x->af(x)f'(x)limlimJimAFF(x)F'(x)5ax-→ax-→a

= ( ) ( ) F x f x ( ) ( )   F f   = (在x与a之间) 当x →a时, A F x f x x a =   → ( ) ( ) (3) lim  = → ( ) ( ) lim F x f x x a 柯西定理 在(a, x)内至少存在点,使 =   = → ( ) ( ) lim F x f x x a ( ) ( ) F x f x  → a, ( ) ( ) lim    F f a   → A. − F(a) − f (a)

这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则.f(x)(x)注 lim(1) limF(x) (0F'(x) (0x-→ax-→af"(x)(= lim（多次用法则）=F"(x) (0x-→a(2)x→a+0,x→a-0,法则成立

注  =      → 0 0 ( ) ( ) (1)lim F x f x x a . (多次用法则) (2) x → a + 0, x → a − 0,  =        = → 0 0 ( ) ( ) lim F x f x x a 法则成立.         → 0 0 ( ) ( ) lim F x f x x a 再求极限来确定未定式的值的方法称为洛必达 法则. 这种在一定条件下通过分子分母分别求导

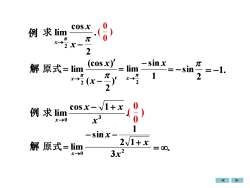
cos x例 求 lim元元x-2 x2(cos x)sinx元解原式=limlimsin12元元元2D2/1+xcosx-例求 limtsx-→01-sinx.2/1+x解原式=lim=8.3x2x-→0

例解 . 2 cos lim2  − → x x x 求 ) 2 ( (cos ) lim2 −  = →   x x x 原式 1 sin lim2 x x − = →  = − 1 . 例解 . cos 1 lim 3 0 x x x x − + → 求 2 0 3 2 11 sin lim x x x x + − − = → 原 式 ) 00 ( ) 00 ( 2 sin  = − = 

定理2 设(1) lim f(x) = 0(或oo),lim F(x) = 0(或0);1X→80(2)当x>N时,f(x)和F(x)可导,且F'(x)±0;'(x)= A (或为);(3) limF(x)x-→0f(x)f'(x)= A(或为),limlim则F(x)x- F'(x)x80证 令x==,则x→ 等价于z→0,用定理1有Z.f(x)>limlimlim1F(x)x→0Z0z-→0HH7

定理2 (1)lim ( ) = 0( ), lim ( ) = 0( ); → → 设 f x 或 F x 或 x x ( ). ( ) ( ) lim ( ) ( ) lim =    = → → A 或 为 F x f x F x f x x x (2)当 x  N时, f (x)和F(x)可 导,且F(x)  0; ( ); ( ) ( ) (3)lim =    → A 或 为 F x f x x 则 证 , 1 z 令x = ( ) ( ) lim F x f x x→             = → z F z f z 1 1 lim 0 则 x →  等价于 z → 0, 用定理1有        −              −       = → 2 2 0 1 1 1 1 lim z z F z z f z

f'(x)limlimAF'(x)-0x→0F注对x→>+8(8),定理2成立;元-arctan x2例求 limx-→>+00sinx1+x?解原式= lim1x→+80·cosx

( ) ( ) lim F x f x x   = → 注 对x → +(−), 定理2成立;               = → z F z f z 1 1 lim 0 = A 例 解 . 1 sin arctan 2 lim x x x − →+   求 x x x x 1 cos 1 1 1 lim 2 2  − + − = →+  原 式 ) 0 0 ( = 1