《高等数学》课程教学资源（PPT课件）第四章 不定积分 4-2 第二节 换元积分法

第二节换元积分法第一换元积分法第二换元积分法小结思考题

第二节 换元积分法 ◼ 第一换元积分法 ◼ 第二换元积分法 ◼ 小结 思考题

cos网= sinx +C第一换元积分法一、今cos2xdxsin2x+C(sin2x) = 2cos2x ± cos2x解决方法 将积分变量换成2x.因为dx2令 t=2x =dx=dt,2C[ cos2xdxsintdtCOS22t =2x11dt一sin2x + C22

 cos2xdx sin2x +C 解决方法 将积分变量换成 令 t = 2x   cos2xdx cost dt 2 1  = = sint + C 2 1 = sin2x + C 2 1 ( ) =  sin2x  cos2x =  cos xdx = sin x +C 2cos2x 2x. 因为 dx = d(2 ) 2 1 x d , 2 1 dx = t t dt 2 1 t = 2x 一、第一换元积分法

注“凑微分”的主要思想是：将所给出的积分凑成积分表里已有的形式,合理选:u=β(x)是微分的关键[ f[p(x)p(x)ax =[ f[p(x)]d@(x)μ=([[ f(u)du l-0(x)第一类换元公式（凑微分法）证(J f[g(x)]p'(x)dx)= f[g(x)]g'(x)(J f(u)du)’=( f(u)du)" u'= f @'(x)p(x)= f(p(x)p(x)

定理  f[(x)](x) dx =  f (u)du 第一类换元公式  f[(x)]d(x) u = (x) （凑微分法） 证  ( f[(x)](x)dx)  x = f [(x)](x)  ( f (u)du)  x =  ( f (u)du)  u ux   = f ((x))(x) u = (x) 可导, 则有换元公式 设 f (u) 具有原函数, 注 “凑微分”的主要思想是:将所给出的积分 凑成积分表里已有的形式,合理选择 是凑微分的关键. u = (x) = f (u)(x) (x)  u=( x)

第一换元积分法若遇到积分f[p(x)lp'(x)dx不易计算时,通过变换u=(x)化为不定积分[ f(u)du来计算,积分后再将u=(x)代入

第一换元积分法 若遇到积分 不易计算时,通过变换 u = (x) 化为不定积分 来计算,  f (u)du 积分后再将 u = (x)  f[(x)](x)dx 代入

sinxdx = -cosx + C例1 求「sin2xdx21U=解法一sin2xdx :2x1(2xsinC2.1uducosu+Csin22ru+11+C"dxcos2x + Cμ+12法二sin 2xdx =I sin x Cos xdx= 2[ sin xd(sin x)=sinX2[ udu= u? + C= (sinx) +C

例1 求  sin2xdx 法一  sin2xdx sin2 d  = x = − cos 2x + C 2 1 法二  sin2xdx  = 2 sin xcos xdx  = 2 sin xd(sin x) = ( x) + C 2 sin u = 2x  = sinudu 2 1 u = sin x = − cosu +C 2 1  2 udu= u + C 2 2 1 解 (2x) x x = − x + C  sin d cos C x x x + + = +  1 d 1   

u+1x"dx+Cu+1法三sin 2xdx =2sinxcosxdxu=cosxudu / Cos xd(cos x12= -u2 + C =-(cosx) + C注同一个积分用不同的方法计算,可能得到表面上不一一致的结果，但是实际上都表示同一族函数

法三  sin2xdx  = 2 sin xcos xdx  = 2 cos xd(cos x) = −( x) + C 2 cos u = cos x  − 2 udu = −u + C 2 同一个积分用不同的方法计算,可能 得到表面上不一致的结果,但是实际上都 表示同一族函数. − 注 C x x x + + = +  1 d 1   

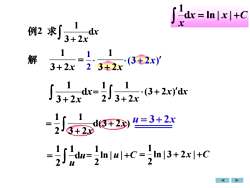
dx = In /x |+CX例2 求dx3+2x111解(3 +2x)3+2x2 3+2x11(3 + 2x)'dxdx:2J3+2x3+2x1u=3+2xd(3+2023+2xIn /3+2x |+C=du==n+2221

例2 求 x x d 3 2 1  + 解 = 3+ 2x 1 x x d 3 2 1  + x x x (3 2 ) d 3 2 1 2 1  +  + =  u u d 1 2 1  = = ln | u | +C 2 1 = ln | 3 + 2x | +C 2 1 d(3 2 ) 3 2 1 2 1 x x + + =  u = 3+ 2x (3 + 2x) 3 2x 1 +  2 1 x x C x = +  d ln | | 1

注对第一换元积分法熟练后，可以不再写出中间变量ru+1V1-3xdx练习了+C(u±-1)u+11-3xd(-30-3x)2 +C33

1 3xdx  − 对第一换元积分法熟练后,可以不再写出 中间变量. = −  ( − x)2 +C 3 1 3 3 2 3 1 注 3 1 − ( 1) 1 d 1 +  − + = +      C x x x d(1− 3x)  = 1− 3x

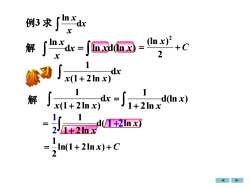
例3求安xInx+CIn xd(解(n x2X1dx山x(1 + 2 ln x)11解d(ln x)x(1 + 2 ln x)+2lnx11(/1+2lnx)2.1+2ln xIn(1+ 2In x)+ C

例3 求 x x x d ln  解 x x x d ln   = ln xd(ln x) C x = + 2 (ln ) 2 x x x d (1 2ln ) 1  + 解 x x x d (1 2ln ) 1  + d(ln ) 1 2ln 1 x x  + = d( ln ) 1 2ln 1 x x  + = = ln(1+ 2ln x) + C 2 1 1+2 2 1

小结常见的凑微分类型有= f(ax+ b)d(ax + b) (a ± 0)[ f(ax + b)dx = -a[ f(ax"+1 + b)x"dx1[ f(axm+1 + b)d(axm+1 + b)a(m+1)[--{a[ f(lnx)=dx =J f(lnx)d(lnx)xJ f(e*)e*dx =] f(e*)d(e*)[ (Vx)=2J (Vx)d(Vx)

常见的凑微分类型有 小结  f (ax + b)dx =  + + f ax b x x m m ( ) d 1  + + + = + + ( )d( ) ( 1) 1 1 1 f ax b ax b a m m m  ( + )d( + )(  0) 1 f ax b ax b a a =  2 d ) 1 ( x x x f  − ) 1 )d( 1 ( x x f =  x x f x d 1 (ln )  f (ln x)d(ln x) =  f e e x x x ( ) d ( )d( ) x x f e e  =  x x f x d ( ) 2 f ( x)d( x) 