《高等数学》课程教学资源（PPT课件）第七章 微分方程 7-2 第二节 可分离变量微分方程

第二节可分离变量微分方程

第二节 可分离变量微分方程

可分离变量的微分方程如果一阶微分方程 F(x,y,J)=0可以写成y= f(x)g(y) 的形式可分离变量的方程或M(x)M2(y)dx + N,(x)N2(y)dy = 0易于化为形式@(x)dxy(y)dy特点 等式的每一边仅是一个变量的函数与这个变量的微分之积两端积分可得通解

 ( y)dy  ( x)dx 如果一阶微分方程 等式的每一边仅是一个变量的函数与这个 可分离变量的方程 y  f (x)g( y) M1(x)M2 ( y)dx  N1(x)N2 ( y)dy  0 或 可以写成 F(x, y, y)  0 的形式, 易于化为形式 特点 变量的微分之积. 两端积分可得通解. 可分离变量的微分方程

可分离变量的方程求通解的步骤是：1.分离变量把方程化为的形式；y(y)dy = @(x)dxy(y)dy = (p(x)dx| +C;2.将上式两边积分其中C为任意常数.由上式确定的函数y=y(x,C)就是方程的通解(隐式通解)这种解方程的方法称为分离变量法

可分离变量的方程求通解的步骤是: 分离变量, 两边积分 其中C为任意常数. y  y(x,C) 就是方程的通解 分离变量法. 1. 把方程化为 ( y)dy  (x)dx 的形式； 2. 由上式确定的函数 (隐式通解). 这种解方程的方法称为 将上式 ( )d ( )d ; ò ò  y y   x x C

例1 求方程 x(1+ y2)dx -y(1+x2)dy=0的通解，xy解分离变量dxd+Xyx两端积分dxdi11+xIn(1=InCn222In(1 + y) = In C(1 + x°):1+y2=C(1+x2）为方程的通解隐式通解

例1 求方程 (1 )d (1 )d 0 的通解. 2 2 x  y x  y  x y  解 分离变量 x x x y y y d 1 d 1 2 2    两端积分   ò y y y d 1 2 ln(1 ) 2 1 ln(1 ) 2 1 2 2  y   x ln(1 ) ln (1 ) 2 2  y  C  x 1 (1 ) 2 2   y  C  x 为方程的通解. lnC 2 1  隐式通解 ò  x x x d 1 2

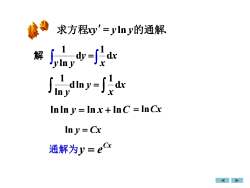
求方程xy=ylny的通解Jlydy=idt解xdlny=-dxInyxInIn y = In x + InC = InCxIn y = Cx通解为y=eCx

解 x x y y y d 1 d ln 1  ò ò ò ò  x x y y d 1 dln ln 1 lnln y  ln x  lnC  lnCx ln y  Cx Cx 通解为y  e 求方程xy   y ln y的通解

注应用问题建立微分方程的方法方法大体有两种第一种方法直接利用物理定律或几何条件列出方程常见的物理定律有力学、热学、光学、电学的定律;第二种方法取小元素分析,然后利用物理定律列出方程(类似于定积分应用中的元素法)

注 应用问题建立微分方程的方法: 方法大体有两种 第一种方法 常见的物理定律有力学、热学、光学、电学 直接利用物理定律或几何条件列出方程, 的定律; 第二种方法 取小元素分析,然后利用物理定律列出 方程(类似于定积分应用中的元素法)

例2衰变问题.衰变速度与未衰变原子含量M成正比已知Mt-o= Mo,求衰变过程中铀含量 M (t)随时间t变化的规律dM解衰变速度由题设条件分离变量dtdMdM=-adt(a>0衰变系数):-2MMdt负号是由于当t增加时M单调减少M =] - Ad,In M=-αt+InC, 即 M = Ce-n,通解代入M|t=o = Mo,得 M。=Ce° = C特解M = M,e-αu衰变规律

两端积分 解 , d d t M 由题设条件 ( 0 ) d d  M   衰变系数 t M t M M d d   d , d ò ò   t M M  , 代入M t0  M0 ln M  t  lnC, 即 0 得 M0  Ce  C t M M e   0 分离变量 负号是由于当 t 增加时M单调减少 , t M Ce   通解 特解 例2 衰变问题.衰变速度与未衰变原子含量M成 正比, , 已知M t0  M0 求衰变过程中铀含量 M (t) 随时间 t 变化的规律.衰变规律 衰变速度

初始条件：例3求游船上的传染病人数.y(0)=1,(12)=3一只游船上有800人一名游客患了某种传染病12小时后有3人发病.由于这种传染病没有早期症状故感染者不能被及时隔离：直升机将在60至72小时将疫苗运到试估算疫苗运到时患此传染病的人数设传染病的传播速度与受感染的人数及未受感染的人数之积成正比，解用y(t)表示发现首例病人后t小时时的感染人的人数,由题意，数,800-可分离变量微分方程dy得= ky(800 - y),其中k>0为比例常数dxdy分离变量= kdt,y(800 - y)

例3 求游船上的传染病人数. 一只游船上有800人, 12小时后有3人发病. 故感染者不能被及时隔离. 设传染病的传播速度与受感染的人数及未受感染的 人数之积成正比. 一名游客患了某种传染病, 由于这种传染病没有早期症状, 直升机将在60至72小时 将疫苗运到,试估算疫苗运到时患此传染病的人数. 解 用 y ( t )表示发现首例病人后 t 小时时的感染人 数, 800  y(t) 表示 t 刻未受感染的人数, 由题意, 得 (800 ), d d ky y x y   其中k > 0为比例常数. 可分离变量微分方程 分离变量 d , (800 ) d k t y y y   y(0)  1, 初始条件: y(12)  3

初始条件dy:kdt.y(0) = 1, y(12) = 3y(800 -y)11即dy = kdt,800800.山1两边积分,得[ln y- In(800 - y)] = kt + Ci:800800(C = e-800C ).通解V:1 + Ce-800kt由初始条件y(0)=1， 得C = 799.再由y(12)=3,7991便可确定出800k~In~ 0.09176.122397800所以y(t) =-0.09176t一1+ 799e

d , (800 ) d k t y y y   即 d d , 800 1 1 800 1 y k t y y          两边积分,得 [ln ln(800 )] , 800 1 C1 y   y  kt  通解 kt Ce y 800 1 800    ( ). 1 800C C e   y(0)  1, 初始条件 y(12)  3 由初始条件y(0)  1, 得C  799.再由y(12)  3, 便可确定出800k  所以 . 1 799 800 ( ) 0.09176t e y t    2397 799 ln 12 1   0.09176

直升机将在60至72小时将疫苗运到,试估算疫苗运到时患此传染病的人数800y(t) =1 + 799e-0.09176t 下面计算t=60,72 小时时的感染者人数800y(60) =-0.09176x60 ~ 188,1 + 799e800y(72) =~385.-0.09176x721 + 799e从上面数字可看出，在72小时疫苗运到时，感染的人数将是60小时感染人数的2倍．可见在传染病流行时及时采取措施是至关重要的

. 1 799 800 ( ) 0.09176t e y t    直升机将在60至72小时将疫苗运到,试估算疫苗 运到时患此传染病的人数. 下面计算t  60,72 小时时的感染者人数 y(60)  y(72)  从上面数字可看出, 在72小时疫苗运到时, 感 染的人数将是60小时感染人数的2倍. 病流行时及时采取措施是至关重要的. 可见在传染 188, 1 799 800 0.09176 60     e 385. 1 799 800 0.09176 72     e