《高等数学》课程教学资源（PPT课件）第九章 多元函数微分法及其应用 9-8 第八节 多元函数的极值与拉格朗日乘数法

第八节多元函数的极值与拉格朗日乘数法多元函数的极值和最值1条件极值拉格朗日乘数法■小结思考题

◼ 多元函数的极值和最值 ◼ 条件极值 拉格朗日乘数法 ◼ 小结 思考题 第八节 多元函数的极值与 拉格朗日乘数法

一、多元函数的极值和最值1.极大值和极小值的定义一元函数的极值的定义：是在一点附近将函数值比大小定义设在点P,的某个邻域,f(P)<(P),则称点P.为函数的极大值点.f(P)为极大值类似可定义极小值点和极小值

一、多元函数的极值和最值 一元函数的极值的定义:是在一点附近 将函数值比大小. 定义 点P0为函数的极大值点. 类似可定义极小值点和极小值. 设在点P0的某个邻域, ( ) ( ), P0 f P  f 为极大值. 则称 ( ) P0 f 1. 极大值和极小值的定义

极值函数的极大值与极小值统称为函数的函数的极大值点与极小值点统称为函数的极值点注多元函数的极值也是局部的,是与P的邻域内的值比较般来说：极大值未必是函数的最大值-极小值未必是函数的最小值有时极小值可能比极大值还大

注 函数的极大值与极小值统称为函数的 函数的极大值点与极小值点统称为函数的 多元函数的极值也是局部的, 一般来说:极大值未必是函数的最大值. 极小值未必是函数的最小值. 有时 , 极值. 极值点. 内的值比较. 是与P0的邻域 极小值可能比极大值还大

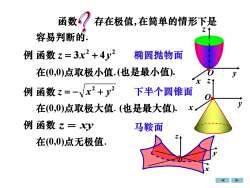
函数存在极值，在简单的情形下是7.容易判断的。例函数z=3x2+4y椭圆抛物面在(0,0)点取极小值.(也是最小值)0yZ.例 函数=2+2下半个圆锥面V在(0,0)点取极大值.（也是最大值)x例 函数 z = xy马鞍面L在(0,0)点无极值

x y z O x y z O 例 2 2 z = 3x + 4y 例 2 2 z = − x + y 例 z = xy 函数 存在极值, 在(0,0)点取极小值. 在(0,0)点取极大值.(也是最大值). 在(0,0)点无极值. 椭圆抛物面 下半个圆锥面 马鞍面 在简单的情形下是 容易判断的. 函数 函数 (也是最小值). 函数 • • x y z O •

2.极值的必要条件定理1(必要条件）设函数z= f(x,y)在点(xo,Jo)具有偏导数,且在点(xo,)处有极值,则它在该点的偏导数必然为零：f,(xo, yo)= 0.fr(xo,yo) = 0,证 不妨设z= f(x,J)在点(xo,Jo)处有极大值,则对于(xo,yo)的某邻域内任意(x,)≠(xo,Jo),都有f(x,y)< f(xo,yo),故当y= yo,x± x,时,有f(x, yo) < f(xo, yo),说明一元函数f(x,y)在x=x,处有极大值必有 f(xo,yo)=0;类似地可证f,(xo,Jo)=0

证 定理1(必要条件) ( , ) ( , ) 0 0 设函数z = f x y 在点 x y 具有 且在点(x0 , y0 )处 则它在该 点的偏导数必然为零: ( , ) 0, f x x0 y0 = ( , ) 0. f y x0 y0 = 偏导数, 有极值, 不妨设 z = f (x, y)在点(x0 , y0 )处 有极大值, 则对于(x0 , y0 )的某邻域内任意( , ) ( , ), 0 0 x y  x y 都有 ( , ) ( , ), 0 0 f x y  f x y , , 故当y = y0 x  x0时 ( , ) ( , ), 0 0 0 有f x y  f x y 说明一元函数 f (x, y0 )在x = x0处 有极大值, 必有 ( , ) 0; f x x0 y0 = ( , ) 0. 类似地可证 f y x0 y0 = 2. 极值的必要条件

推广 如果三元函数u= f(x,y,z)在点P(xo,Jo,z)具有偏导数,则它在P(xoyo,zo)有极值的必要条件为f,(xo, Jo,zo) = 0,fx(xo, yo,zo) = 0,f.(xo,Yo,zo) = 0.仿照一元函数，凡能使一阶偏导数同时为零的点,均称为函数的驻点，注驻点极值点I如,点(0,0)是函数z =xy的驻点，但不是极值点如何判定一个驻点是否为极值点

推广 如果三元函数 ( , , ) ( , , ) 0 0 0 u = f x y z 在点P x y z 具有偏导数,则它在 ( , , ) 0 0 0 P x y z 有极值的必要条件 为 ( , , ) 0, f x x0 y0 z0 = ( , , ) 0, f y x0 y0 z0 = ( , , ) 0. f z x0 y0 z0 = 均称为函数的 驻点 极值点 仿照一元函数,凡能使一阶偏导数同时为零的 点, 驻点. 如何判定一个驻点是否为极值点 如, 点(0,0)是函数z = xy的 驻点, 但不是极值点. 注

3.极值的充分条件定理2(充分条件）设函数z=f(x,J)在点(xo,Jo)的某邻域内连续,有一阶及二阶连续偏导数又 f,(xo,yo)= 0, f,(xo,yo)= 0,令 fx(xo,yo)= A, Jx,(Xo,Jo)= B, fm,(Xo,yo) = C,则f(x,y)在点(xo,Jo)处是否取得极值的条件如下:(1）AC-B2>0时有极值,当A0时有极小值；(2) AC －B2<0时没有极值;(3)AC-B2=0时可能有极值,也可能无极值

定理2(充分条件) ( , ) ( , ) 0 0 设函数z = f x y 在点 x y 的某邻域内连续,有一阶及二阶连续偏导数, ( , ) 0, 又 f x x0 y0 = ( , ) 0, f y x0 y0 = ( , ) , 令 f xx x0 y0 = A ( , ) , f xy (x0 , y0 ) = B, f yy x0 y0 = C ( , ) ( , ) 0 0 则f x y 在点 x y 处是否取得极值的条件如下: (1) AC − B 2  0时 有极值, 当A  0时 有极大值, 当A  0时 有极小值; (2) AC − B 2  0时 没有极值; (3) AC − B 2 = 0时 可能有极值,也可能无极值. 3.极值的充分条件

求函数z=f(x,y)极值的一般步骤第一步fr(x,y)=0解方程组f,(x,y)= 0求出实数解，得驻点第二步 对于每一个驻点(xo,Jo),求出二阶偏导数的值A、B、C第三步定出AC－B的符号再判定是否是极值

求函数 z = f (x, y) 极值的一般步骤: 第一步 解方程组    = = ( , ) 0 ( , ) 0 f x y f x y y x 求出实数解,得驻点. 第二步 对于每一个驻点 ( , ), 0 0 x y 求出二阶偏导数的值 A、B、C. 第三步 定出 2 AC − B 的符号, 再判定是否是极值

例1 求函数f(x,y)=3axy-x3-y (a>0)的极值。, = 3ay - 3x2 = 0一 驻点(0,0),(a,a)解, = 3ax -3y? = 0又 fxx =-6x, Jx,= 3a,y, =-6y.在点(0,0)处,AC-B2 =-9αa2 <0故f(x,J)在(0,0)无极值;在点(a,a)处,AC-B2=27α2 0<且A=-6a<0故f(x,J)在(a,a)有极大值,即 f(a,a)=a3

例1 解 又 在点(0,0)处, 在点(a,a)处, ( , ) 3 ( 0) 3 3 求函数 f x y = axy − x − y a      = − = = − = 3 3 0 3 3 0 2 2 f ax y f ay x y x  驻点(0,0),(a,a). f xx = f xy = f yy = 2 2 AC − B = −9a 故 f ( x, y) 2 2 AC − B = 27a 且A = −6a 故 f ( x, y) 即 ( , ) . 3 f a a = a 的极值.  0 在(0,0)无极值; 0  在(a,a)有极大值,  0 − 6x, 3a, − 6 y

然子求由方程x2+y2+z2-2x+2y-4z-10=0确定的函数z=f(x,y)的极值解 法一 将方程两边分别对x,y求偏导数2x+2zz-2-4z=02y+2z·z, +2-4z, = 0由函数取极值的必要条件知,驻点为P(1,-1)将上方程组再分别对x,y求偏导数B=z"lp=0, C=z'2-z

2 + 2   − 2 − 4  = 0 x x x z z z 解 求由方程 2 2 4 10 0 2 2 2 x + y + z − x + y − z − = 确定的函数z = f (x, y)的极值. 将方程两边分别对x, y求偏导数,  2 y + 2zz  y + 2 − 4z  y = 0   由函数取极值的必要条件知,驻点为 P(1,−1), 将上方程组再分别对x, y求偏导数, , 2 1 | z A z xx P − =  = =  | = 0, xy P B z , 2 1 | z C z yy P − =  = 法一