《高等数学》课程教学资源（PPT课件）第十章 重积分 10-04 第四节 重积分的应用

第四节重积分的应用一、立体体积二、曲面的面积三、 物体的质心四、物体的转动惯量五、物体的引力

第四节 重积分的应用 一、立体体积 二、曲面的面积 三、物体的质心 四、物体的转动惯量 五、物体的引力

1.能用重积分解决的实际问题的特点分布在有界闭域上的整体量所求量是对区域具有可加性2.用重积分解决问题的方法·用微元分析法（元素法·从定积分定义出发建立积分式3.解题要点画出积分域、选择坐标系、确定积分序、定出积分限、计算要简便

1. 能用重积分解决的实际问题的特点 所求量是 对区域具有可加性 • 从定积分定义出发建立积分式 • 用微元分析法 (元素法) 分布在有界闭域上的整体量 3. 解题要点 画出积分域、选择坐标系、确定积分序、 定出积分限、计算要简便 2. 用重积分解决问题的方法

立体体积A曲顶柱体的顶为连续曲面 z= f(x,y),(x,V)E D则其体积为V= J, f(x,y)dxdy占有空间有界域Q的立体的体积为JV=dxdydzC

一、立体体积 • 曲顶柱体的顶为连续曲面 则其体积为 • 占有空间有界域的立体的体积为 V dxdydz  = 

例1求曲面 S,:z=x2+y2+1任一点的切平面与曲面S,:z=x2+y"所围立体的体积V.分析曲面S,在点（xo，Jo，z）的切平面方程为z = 2x,x+2yoy+1-x - y?它与曲面 z=x2+y'的交线在xoy面上的投影域为D(x-x) +(y-jo)=1用二重积分求体积V解 V= [,[2x,x+2yoj+1-x?-y2-x? - y2] dxd y= JJ,[ 1-((x-xo)+(y-yo))]dxdyAx-x=rcose, y-y,=rsine元2元r3dr:del三元一20

任一点的切平面与曲面 所围立体的体积V. 解 S1 的切平面方程为 2 2 0 0 0 0 z x x y y x y = + + − − 2 2 1 它与曲面 的交线在xoy面上的投影域为D 2 2 0 0 ( ) ( ) 1 x x y y − + − =  d d  D V x y =  2 2 − − x y 2 2 0 0 0 0 2 2 1 x x y y x y + + − −  1 d d D = − x y  ( ) 2 2 0 0 ( ) ( ) x x y y − + − 0 0 令 x x r y y r − = − = cos , sin   2  = 在点 例1 求曲面 =  − 2 1 3 0 0 d d r r     分析 曲面 用二重积分求体积V

例2又求半径为α的球面与半顶角为α的1Z2a内接锥面所围成的立体的体积iM分析在球坐标系下空间立体所占区域为r0≤r≤2acosΦ2:0≤@≤α用三重积分求VyO0≤0≤2元dv=r sin@ded@dr则立体体积为2acosgV= JJJ,dxd ydz=|2 dr"del'sing do]10C34元a1-cos*α)3

x o y z 2a 例2 求半径为a的球面与半顶角为的 内接锥面所围成的立体的体积. 分析 在球坐标系下空间立体所占区 域为  : 则立体体积为 V x y z d d d  =  2 cos 2 0 d a r r   3 4 4 ( 1 cos ) 3  a = −  0 2 cos  r a  0     0 2     0 sin d     2 0 d  =   2 d sin d d d v r r =      r M 用三重积分求V

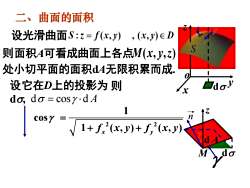
曲面的面积设光滑曲面S:z=f(x,y),(x,y)ED则面积A可看成曲面上各点M(x,y,z)处小切平面的面积dA无限积累而成设它在D上的投影为则Xdo, do =cosy.dA1ncosY1+ f2(x,y)+ f,(x,y)M1do

 M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积A可看成曲面上各点 M x y z ( , , ) 处小切平面的面积dA无限积累而成. 设它在D上的投影为 d, d = cos d A 2 2 1 cos 1 ( , ) ( , ) x y f x y f x y  = + + 则   M n  d

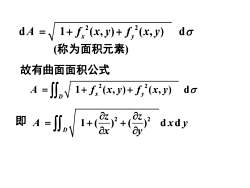
dgdA =/ 1+ f(x,J)+ f?(x,y)(称为面积元素)故有曲面面积公式A = [J, 1+ f?(x,y)+ f,'(x,y)dgOz.Oz.即 A=J,1dxdydxd

故有曲面面积公式 2 2 1 ( , ) ( , ) d x y D A f x y f x y = + +   2 2 1 ( ) ( ) d d D z z A x y x y   = + +   即  2 2 d 1 ( , ) ( , ) d A f x y f x y = + + x y  (称为面积元素)

若光滑曲面方程为x=g(y,z)，(y,z)eD则有axax)2dydz1+(ayazD若光滑曲面方程为 y=h(z,x)，(z,x)eD,x则有ayay>2dzdx1+azax

2 2 1 ( ) ( ) d d y y A z x z x   = + +    若光滑曲面方程为 ( , ) , ( , ) , z x y h z x z x D =  则有 D z x 若光滑曲面方程为 ( , ) , ( , ) , y z x g y z y z D =  则有 D y z

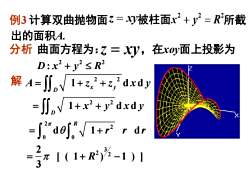
例3计算双曲抛物面=xy被柱面x2+y2=R"所截出的面积A.分析日曲面方程为：z=XV，在xoy面上投影为D:x? + y?≤R?解 A=J,1+z?+z, dxdy=JJ,1+x +y?dxdy2元de/ 1+r2 r dr2[(1+R’)%-1) ]元3

例3 计算双曲抛物面 被柱面 所截 分析 曲面方程为： ，在xoy面上投影为 2 2 1 d d x y D A z z x y = + +  2 2 1 d d D = + + x y x y 2 2 0 0 d 1 d R r r r  = +    3 2 2 2 [ ( 1 ) 1 ) ] 3 = + −  R 出的面积A. 解 2 2 2 D x y R : + 

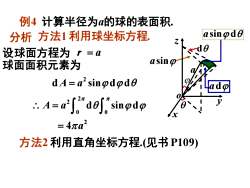
例4i计算半径为的球的表面积asin@de方法1利用球坐标方程分析7.de设球面方程为r=aasing球面面积元素为dA= a’ sinpdpdeadp27y1"del"singdpA== 4元a2方法2利用直角坐标方程.（见书P109)

例4 计算半径为a的球的表面积. 分析 设球面方程为 r a = 球面面积元素为 2 d sin d d A a =    2 2 0 0 A a d sin d    =      2 = 4a asin ad 方法2 利用直角坐标方程.(见书P109) 方法1 利用球坐标方程.   a x y z o d asin d  