《高等数学》课程教学资源（PPT课件）第十二章 无穷级数 12-06 第七节 傅里叶（Fourier）级数（series）

第七节傅里叶(Fourier)级数(series）问题的提出三角函数系的正交性函数展开成傅里叶级数正弦级数或余弦级数■小结思考题

第七节 傅里叶（Fourier)级数(series) ◼ 问题的提出 ◼ 三角函数系的正交性 ◼ 函数展开成傅里叶级数 ◼ 正弦级数或余弦级数 ◼ 小结 思考题

上一节详细研究了一种重要的函数项级数幕级数.下面研究另一种重要的函数项级数：：傅里叶级数·这种级数是由于研究周期现象的需要而产生的．它在电工、力学和许多学科中都有很重要的应用。傅里叶（Fourier,1768-1830）法国数学家和物理学家法国科学院院士，英国皇家学会会员

2 上一节详细研究了一种重要的函数项级数: 幂级数. 下面研究另一种重要的函数项级数: 这种级数是由于研究周期现象的需要而 产生的. 它在电工、力学和许多学科中都有很 重要的应用. 傅里叶(Fourier,1768-1830) 法国数学家和 物理学家. 法国科学院院士,英国皇家学会会员. 傅里叶 级数

历史朔源1757年，法国数学家克莱罗在研究太阳引起的摄动时，大胆地采用了三角级数表示函数：0f(x) =A,+2E A, cos nxn=lS2其中A,f(x)cos nxdx=2元J1759年,拉格朗日在对声学的研究中也使用了三角级数．1777年,欧拉在研究天文学的时候用三角函数的正交性得到了将函数表示成三角级数时的系数也就是现今教科书中傅里叶级数的系数

3 1757年,法国数学家克莱罗在研究太阳引起 的摄动时,   = = + 1 0 ( ) 2 cos n f x A An nx 1759年,拉格朗日在对声学的研究中也使用了 三角级数. 用三角函数的正交性得到了将函数表示成三角 1777年,欧拉在研究天文学的时候, 级数时的系数,也就是现今教科书中傅里叶级数 的系数. 大胆地采用了 历史朔源 三角级数表示函数:  =   2 0 ( )cos 2 1 其中An f x nxdx

在历史上，三角级数的出现和发展与求解微分方程是分不开的1753年，丹·贝努利首先提出将弦振动方程的解表示为三角级数的形式,这为函数的傅里叶展开这个纯数学问题奠定了物理基础，促进了分析学的发展1822年，傅叶在《热的解析理论》一书中对于欧拉和贝努利等人就一些孤立的，特殊的情形所采用的三角级数方法进行加工处理，发展成一般理论

4 微分方程是分不开的. 析学的发展. 形所采用的三角级数方法进行加工处理, 1753年, 的解表示为三角级数的形式,这为函数的傅里叶 展开这个纯数学问题奠定了物理基础,促进了分 在历史上, 丹贝努利首先提出将弦振动方程 1822年,傅里叶在《热的解析理论》一书中 对于欧拉和贝努利等人就一些孤立的，特殊的情 发展成 一般理论. 三角级数的出现和发展与求解

一、问题的提出在自然界和人类的生产实践中，周而复始的现象，周期运动是常见的如行星的飞转，飞轮的旋转，蒸气机活塞的往复运动物体的振动,声、光、电的波动等数学上，用周期函数来描述它们.最简单最基本的周期函数是正弦型函数角频率谐函数Asin(0t+?2元简谐波周期振幅时间初相简谐振动0A

5 一、问题的提出 在自然界和人类的生产实践中,周而复始 的现象, 周期运动是常见的. 如行星的飞转,飞轮的旋转,蒸气机活塞的 往复运动,物体的振动,声、光、电的波动等. 数学上,用周期函数来描述它们.最简单最基本 的周期函数是 谐函数 Asin( t + ) 周期  2 振幅 时间 角频率 初相 简谐波 简谐振动 正弦型函数

除了正弦函数外，常遇到的是非正弦周期函数-1,当-元≤t<0较复杂的如矩形波u(t)=1,当0≤t<元周期现象u101元元！1o0分解不同频率正弦波逐个叠加1元元元福元元sin3tsin 9t.sint.sin5t9344Ve

6 如矩形波      − −   =   t t u t 1, 0 1, 0 ( ) 当 当 不同频率正弦波 sin , 4 t  sin3 , 3 1 4  t  sin5 , 5 1 4  t  sin7 , 7 1 4  t  除了正弦函数外,常遇到的是非正弦周期函数, 较复杂的 周期现象  分解 逐个叠加 sin9 , 9 1 4  t  O t u 1 − 1 − 

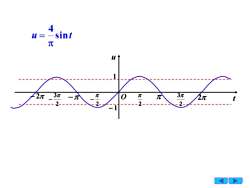
4sintu=一元u3元3元元2元元0元一元2元?222中-1A

7 1 − 1 O t u − 2 − 2 2  − 2   2 3 − 2 3

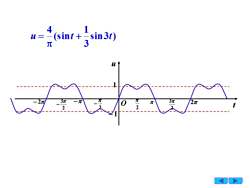
(sint + =sin3t)u=3元元3元2元I元02

8 O t u 1 − 1 − 2 − 2 2  − 2   2 3 − 2 3

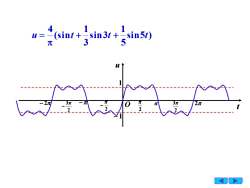
(sint +=sin3t +=sin5t)u=35元3元2元O元

9 O t u 1 − 1 − 2 − 2 2  − 2   2 3 − 2 3

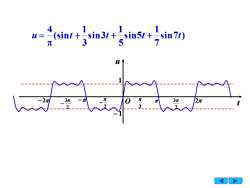
(sint +=sin3t +=sin5t +=sin7t)U=35元u1

10 O t u 1 − 1 − 2 − 2 2  − 2   2 3 − 2 3