《高等数学》课程教学资源（PPT课件）第十二章 无穷级数 12-08 第八节 周期为2l的周期函数的傅里叶级数

第八节周期为21的周期函数的傅里叶级数傅里周期为21 的周期函数的叶级数典型例题■小结思考题

◼ 周期为2l 的周期函数的 傅里 叶级数 ◼ 典型例题 ◼ 小结 思考题 第八节 周期为2l 的周期函数的 傅里叶级数

以2伪周期的傅氏级数2元元: T = 2l,代入傅氏级数中018Qo(a, cosnox+b, sinnox)2n=1定理设周期为21l的周期函数f(x)满足收敛定理的条件.则它的傅里叶级数展开式为8n元xn元xf(x)="+E(an+bsin.cos2n=

T = 2l,  = = T   2 定理 ( cos sin ) 2 ( ) 1 0 l n x b l n x a a f x n n n     = = + + ( cos sin ) 2 1 0 a n x b n x a n n  n    = + + 代入傅氏级数中   l  一、以2l为周期的傅氏级数 设周期为2l 的周期函数 f (x)满足收敛 定理的条件,则它的傅里叶级数展开式为

其中系数an,b,为n元x[a,=,] f(x)cosdx(n = 0,1,2,..)nx=f(x)sindx(n = 1,2,...)(1) 如果f (x)为奇函数,则有8nxEb, sinf(x)=n=1nx其中系数 b,=”dx (n = 1,2,3, ...).1

其中系数an , bn为 x l n x f x l a l l n ( )cos d 1 − =  x l n x f x l b l l n ( )sin d 1 − =  则有   = = 1 ( ) sin n n l n x f x b  (n = 1,2,3, ). (n = 0,1,2, ) (n = 1,2, ) x l n x f x l b l n ( )sin d 2 0 =  (1) 如果 f (x)为奇函数, 其中系数   

(2) 如果,f(x)为偶函数,则有n元xf(x)="+a..cos1n=1nx2尔(n = 0,1,2, ..)dx其中系数ancoS=1注以2为周期的函数的傅里叶级数有一样的收敛定理,只是把元改为l

则有   = = + 1 0 cos 2 ( ) n n l n x a a f x  x (n = 0,1,2, ) l n x f x l a l n ( )cos d 2 0 =  注 只是把 改为 偶函数, l. (2) 如果 f (x)为 其中系数 以2l为周期的函数的傅里叶级数有一样 的收敛定理

典型例题二、将f(x)周期延拓例在[-1,1]上把f(x)=x展开为傅里叶级数.1=1解f(x)为偶函数,展开为余弦级数2a-S.f(x)dx =dxX31nx- ()coscosnxdxXdxn1S4(n = 1,2,3, )-1)(n元)孔4(-1)">得 x2=x e[-1,1]十cosn元x23n元n=1

二、典型例题 解 l = 1  = l f x x l a 0 0 ( )d 2 3 2 2 d 1 0 2 = =  x x x l n x f x l a l n ( )cos d 2 0 =   = 1 0 2 2 x cos nxdx 2 ( ) 4 ( 1) n n = − (n = 1,2,3, ) 得 n x n x n n   cos 4 ( 1) 3 1 1 2 2 2   = − = + x [−1,1] 将f (x)周期延拓 例 f (x)为偶函数,展开为余弦级数 2 在[ 1,1] ( ) . − = 上把f x x 展开为傅里叶级数

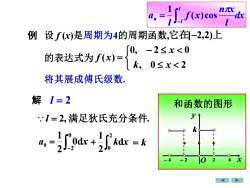
nTx=f(x)cosdxa,n1例 设,f(x)是周期为4的周期函数,它在[-2,2)上[0,-2≤x<0的表达式为,f(x)=k, 0≤x<2将其展成傅氏级数解 [=2和函数的图形y：l=2.满足狄氏充分条件FOdx +kdx = k2 Jo2J7

解 l = 2, 满足狄氏充分条件. a0 = = k dx l n x f x l a l l n − =  ( )cos 1 l = 2 − 0 2 0d 2 1 x  + 2 0 d 2 1 k x 例 将其展成傅氏级数.      −   = , 0 2 0, 2 0 ( ) k x x f x 它在[−2,2)上 f (x)的图形 k O x y − 4 − 2 2 4 和函数的图形 k O x y − 4 − 2 2 4 设 f (x)是周期为4的周期函数, 的表达式为

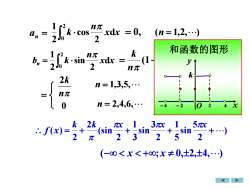
1n元= 0,k.cosxdx(n = 1,2,..)2n22 Jo和函数的图形k2n元k·sin1xdx22 Jon元2kn =1,3,5, .n元n = 2,4,6, .:01024-2X42kk13元x15元XTx(sinsinsin: f(x) =+.222325元(-80 < x< +80; x ± 0,±2,±4,.)

  2 0 d 2 cos 2 1 x x n k  = 0,  =  2 0 d 2 sin 2 1 x x n bn k  (1 cos  )  n n k = −    = ) 2 5 sin 5 1 2 3 sin 3 1 2 (sin 2 2  ( ) = + + + + k k x x x f x     (−  x  +; x  0,2,4, ) an = (n = 1,2, ) n = 1,3,5,  n 2k 0 n = 2,4,6,  和函数的图形 k O x y − 4 − 2 2 4

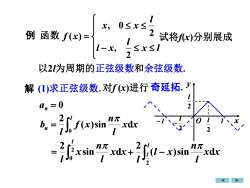
10≤x≤x,2例 函数 f(x)=试将(x)分别展成1x≤l1-x.L2以2为周期的正弦级数和余弦级数解(1)求正弦级数.对f(x)进行奇延拓.an =02n元01b,=2sinxdx222n元n元xdx+xdxSsin1e2

例 函数      −     = x l l l x l x x f x 2 , 2 , 0 ( ) 试将f(x)分别展成 以2l为周期的正弦级数和余弦级数. 解 (1)求正弦级数.  = l n x x l n f x l b 0 ( )sin d 2  an = 0  = 2 0 sin d 2 l x x l n x l  x x l n l x l l l ( )sin d 2 2  + −  奇延拓. O x y 2 l 2 l l 2 l − l − 对f (x)进行

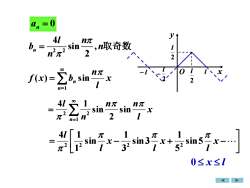
a,=0y41n元n取奇数1sin1P2n元2801n元Zbf(x) =sinX211n=10411n元n元ZsinsinX2221元nn=11141元元元sin3imx+imX232111元0≤x≤l

2 2 4 sin , 2 n l n b n n   = 取奇数 x l n f x b n n  ( ) sin 1   = =   = = 1 2 2 sin 2 sin 4 1 n x l n n n l          = − + x − l x l x l l     sin5 5 1 sin3 3 1 sin 1 4 1 2 2 2 2 0  x  l an = 0 O x y 2 l 2 l l 2 l − l −

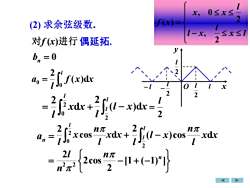
10≤x≤X,2f(x)=(2)求余弦级数11-x,≤x≤I2对f(x)进行偶延拓.yb, = 012/- ()de7101-1x222 xdx+Lx)dx Jo2212 2n元eln元2(l.xdxxdx +)cosxxcosan=11 Jo221n元(-1)"]2cos222n元

(2) 求余弦级数. bn = 0  = l f x x l a 0 0 ( )d 2      −     = x l l l x l x x f x 2 , 2 , 0 ( )  = + 2 0 d 2 l x x l  − l l l x x l 2 ( )d 2 偶延拓. an =       = −[1+ (−1) ] 2 2cos 2 2 2 n n n l    − l l x x l n l x l 2 ( )cos d 2  +  x x l n x l l cos d 2 2 0  2 l = O x y 2 l 2 l l 2 l − l − 对f (x)进行