《高等数学》课程教学资源（PPT课件）第十一章 曲线曲面积分 11-02 第二节 对坐标的曲线积分

第二节对坐标的曲线积分对坐标的曲线积分的概念与性质对坐标的曲线积分的计算法两类曲线积分之间的联系小结思考题

第二节 对坐标的曲线积分 ◼ 对坐标的曲线积分的概念与性质 ◼ 对坐标的曲线积分的计算法 ◼ 两类曲线积分之间的联系 ◼ 小结 思考题

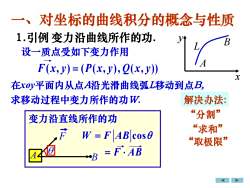
一、对坐标的曲线积分的概念与性质1.引例变力沿曲线所作的功VBL设一质点受如下变力作用AF(x, y)=(P(x,y),Q(x,y)x在xov平面内从点A沿光滑曲线弧L移动到点B求移动过程中变力所作的功W解决办法：“分割”变力沿直线所作的功“求和”FW = F|ABcosa“取极限”白= F.ABA4B

一、对坐标的曲线积分的概念与性质 1.引例 变力沿曲线所作的功. 设一质点受如下变力作用 在xoy平面内从点A沿光滑曲线弧L移动到点B, A B L x y W F AB = cos “分割” “求和” “取极限” 变力沿直线所作的功 求移动过程中变力所作的功W. 解决办法: A =  F AB B F  F x y P x y Q x y ( , ) ( ( , ), ( , )) =

1)“分割”把L分成n个小弧段，F沿Mk-MF(5k,nk)y为△Wk，则所做的功为B1Ayk12W=AWAxkkk=1A2)“求和”x用有向线段Mk-M =(Axk,Ayk)M-M有向小弧段在Mk-iM,上任取一点近似代替，(k,nk),则有AW,~ F(5k,nk).Mk-M= P(5k,nk)Ax, +Q(5k,nk)Ayk

M k −1 Mk A B x y 1) “分割”. 2) “求和” L 把L分成n个小弧段, 有向小弧段 近似代替, 则有 k k ( , ) ( , ) P x Q y k k k k =  +      所做的功为 F 沿 k 1 ( , ) W F M M k k k k      − ( , ) F k k   1 n k k W W = =   则 用有向线段 在 上任取一点 k  y k x

Z [ P(5,nk)Axe +Q(Sk, nk)Aye ]W~k=13)“取极限”Z[P(5h, nk)4x, +Q(5h, nk)4yk]W = lim→0k=1F(5k,nk)(其中为 n个小弧段的VB最大长度)1DykAxkx

3) “取极限” 1 n k W =    P x Q ( , ) ( , )    k k k k k k  +  ξ y  0 1 lim n k W → = =   ( , , P k k k k k k ξ η )Δx Q( + ξ η )Δy  M k −1 L Mk A B x y ( , ) F k k  k  y k x (其中 为 n 个小弧段的 最大长度)

2.定义．设L为xoy平面内从A到B的一条有向光滑弧，在L上定义了一个向量函数F(x,y)=(P(x,y),Q(x,y)若对L的任意分割和在局部弧段上任意取点n极限Z[1limP(5k,nk)Ax,+Q(5k,nk)Ayk→0k=1记作P(x,y)dx +Q(x,y)dy都存在

2.定义. 设L为xoy平面内从A到B的一条有向光滑 弧, 若对L的任意分割和在局部弧段上任意取点, ( , )d ( , )d 都存在, L P x y x Q x y y +   ( , ) P x k k k    ( , ) Q y k k k +     1 n k= lim →0  在L上定义了一个向量函数 极限 记作

则称此极限为函数 F(x,J)在有向曲线弧L上对坐标的曲线积分，或第二类曲线积分其中，P(x,y)，Q(x,y)称为被积函数L称为积分弧段或积分曲线nZP(Ek,nk)Axk P(x, y)dx= lim10k=1称为对x的曲线积分：nZ[, Q(x, y)dy= limQ(Sk,nk)Ayk 20k=1称为对的曲线积分

( , )d L P x y x  0 1 lim ( , ) , n k k k k P x    → = =   ( , )d L Q x y y  0 1 lim ( , ) , n k k k k Q y    → = =   称为对x的曲线积分; 称为对y的曲线积分. 在有向曲线弧L上 对坐标的曲线积分, 则称此极限为函数 或第二类曲线积分. 其中, L称为积分弧段或积分曲线. 称为被积函数

ds=(dx,dy),对坐标的曲线积分也可写作若记(, F.ds = (, P(x,y)dx +Q(x,y)dy类似地，若为空间曲线弧，记ds=(dx,dy, dz)F(x,y,z) = (P(x,y,z), Q(x, y,z), R(x,y,z)[. F -d s = [ P(x, y,z)dx+Q(x, y,z)dy + R(x, y,z)dz

若为空间曲线弧, 记 若记 d (d , d ) s x y = ,对坐标的曲线积分也可写作 d ( , )d ( , )d L L F s P x y x Q x y y  = +   F x y z P x y z Q x y z R x y z ( , , ) ( ( , , ), ( , , ), ( , , )) = 类似地, d (d , d , d ) s x y z =

3. 性质(1）若L可分成k条有向光滑曲线弧L, (i=1,...,k)则(, P(x,y)dx +Q(x, y)dykZIP(x,y)dx + Q(x,y)dyJLi=1(2)用L一表示L的反向弧，则_ P(x, y)dx +Q(x,y)dy = -(, P(x,y)dx +Q(x, y)dy说明·对坐标的曲线积分必须注意积分弧段的方向！，定积分是第二类曲线积分的特例

3. 性质 (1) 若L可分成k条有向光滑曲线弧 ( , )d ( , )d L P x y x Q x y y +  1 ( , )d ( , )d i k L i P x y x Q x y y = = +  (2) 用L－ 表示L的反向弧, 则 ( , )d ( , )d L = − + P x y x Q x y y  则 • 定积分是第二类曲线积分的特例. 说明 • 对坐标的曲线积分必须注意积分弧段的方向!

二、对坐标的曲线积分的计算法定理若P(x,y),Q(x,y)在有向光滑弧L上有定义且x=(t) t:α→β,则曲线积分连续，L的参数方程为y=y(t)存在,且有[. P(x,y)dx + Q(x, y)dy[( P[0(t), y (t) '(t)+2p(t), y(t)'(t)dt证明下面先证[, P(x,y)dxP[p(t), y (t)lp'(t)dta

二、对坐标的曲线积分的计算法 定理 在有向光滑弧L上有定义且 L的参数方程为 ( ) ( ) x t y t    =   = t : ,   → 则曲线积分  P t t [ ( ), ( )]   =    ( )t +Q t t [ ( ), ( )]    ( )t dt 连续, 证明 下面先证 P t t t [ ( ), ( )] d   =    ( )t 存在,且有

nZF[, P(x,y)dx= limP(5,,n:)Ax;根据定义2-→0i=1Ti，由于设分点 X,对应参数 ti,点（s;,n)对应参数Ax; = x; -x;-F p(t,) -p(ti-1)= p'(t)At,nZP[(t,),V(t,)]0'(t)At, P(x, y)dx= lim-0i=1所以βp'(t)连续因为L为光滑弧，nZ1=limP[p(t,), y(t,)p'(t,)△t2-0i=1P[p(t), y(t)lp'(t)dt同理可证S,Q(x, y)dy= f° Q[p(t), y (t)l y'(t) dt

设分点 对应参数 根据定义 i x , i t , i  由于 i i i 1 x x x  = − − 1 ( ) ( ) i i   t t − = − ( )i i =      t P t t t [ ( ), ( )] d   =    0 1 lim [ ( ), ( )] n i i i P      → = =  ( )i i     t 0 1 lim [ ( ), ( )] n i i i P      → = =  ( )i i    t ( )t 0 1 lim ( , ) n i i i i P x    → = =   对应参数 因为L为光滑弧, 同理可证 Q t t t [ ( ), ( )] d   =     ( )t 点 连续