《高等数学》课程教学资源（PPT课件）第十章 重积分 10-01 第一节 二重积分的概念与性质

第一节二重积分的概念与性质问题的提出二重积分的概念二重积分的性质■小结思考题

第一节 二重积分的概念与性质 ◼ 问题的提出 ◼ 二重积分的概念 ◼ 二重积分的性质 ◼ 小结 思考题

问题的提出1·曲顶柱体的体积柱体体积=底面积×高平顶.特点：z= f(x,y柱体体积=？曲顶.特点：日曲顶柱体

柱体体积=底面积× 高 特点：平顶. 柱体体积=？ 特点：曲顶. z = f (x, y) D １．曲顶柱体的体积 一、问题的提出 曲顶柱体

“分割、求和、取求曲顶柱体的体积采用极限”的方法，如下动画演示。密放

播放 求曲顶柱体的体积采用 “分割、求和、取 极限”的方法，如下动画演示．

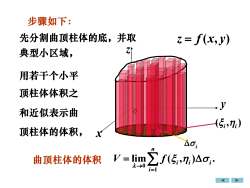
步骤如下：先分割曲顶柱体的底，并取z= f(x,y)Zt典型小区域用若干个小平顶柱体体积之y和近似表示曲(Si,n:)顶柱体的体积，△0;nZf(5,n,)A0.V = lim曲顶柱体的体积2-0i-1

步骤如下： 用若干个小平 顶柱体体积之 和近似表示曲 顶柱体的体积， x z y o D z f x y = ( , )  i • ( , ) i i   先分割曲顶柱体的底，并取 典型小区域， 0 1 lim ( , ) . n i i i i V f     → = 曲顶柱体的体积 =  

2.求平面薄片的质量设有一平面薄片占有xoy面上的区域D，在点(x,J)处的面密度为p(x,y)，假定p(x,y)在D上连续,平面薄片的质量为多少？将薄片分割成若干小块(Si,n:)取典型小块，将其近似看作均匀薄片，所有小o;块质量之和近似等于olxZA薄片总质量M = limp(5i,n:)A,.2-→0i=1

2．求平面薄片的质量  i • ( , ) i i   将薄片分割成若干小块， 取典型小块，将其近似 看作均匀薄片，所有小 块质量之和近似等于 薄片总质量. 0 1 lim ( , ) . n i i i i M      → = =   x y o 设有一平面薄片占有 xoy 面上的区域 D ，在点 ( , ) x y 处的面密度为 ( , ) x y ，假定 ( , ) x y 在 D 上连续，平面薄片 的质量为多少？

两个问题的共性：(1）解决问题的步骤相同“分割、求和、、取极限”(2）所求量的结构式相同曲顶柱体体积：V = limE"=f(Srn)Ag)20平面薄片的质量：E"--p(SknAoM = lim-→0

两个问题的共性： (1) 解决问题的步骤相同 (2) 所求量的结构式相同 “分割、求和、取极限” 1 0 lim ( , ) n M k k k k  =  →  =     曲顶柱体体积: 平面薄片的质量: 1 0 lim ( , ) n k k k k V f  =  →  =   

二、二重积分的概念定义 设f(x,y)是有界闭区域D上的有界函数：将闭区域D任意分成n个小闭区域△i，△2，，△,，其中△,表示第i个小闭区域也表示它的面积，在每个△；上任取一点(Si,n)，作乘积f(S,,n)△oi，(i=1,2,,n),Zf(5i,n;)Ao,并作和i1

定义 设 f x y ( , )是有界闭区域 D 上的有界函数， 将 闭 区 域 D 任 意 分 成 n 个 小 闭 区 域  1 ， 2  , ， n ，其中 i 表示第 i个小闭区域， 也 表 示 它 的 面 积 ， 在 每 个  i 上 任 取 一 点 ( , )  i i ，作乘积 ( , ) i i f    i，( 1,2, , ) i n = ， 并作和 1 ( , ) n i i i i f    =   ， 二、二重积分的概念

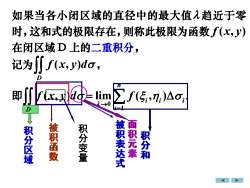
如果当各小闭区域的直径中的最大值九趋近于零时，这和式的极限存在，则称此极限为函数f(x,y)在闭区域D上的二重积分SJ f(x,y)do,记为0Zf(s,n:)Ao;即00Fxdg=lim0D被积表达式面积元素被积函数积分变量积分区域积分和

积分区域 如果当各小闭区域的直径中的最大值 趋近于零 时，这和式的极限存在，则称此极限为函数 f (x, y ) 在闭区域 D 上的二重积分， 记为 ( , ) D f x y d  ， 即 ( , ) D f x y d  0 1 lim ( , ) n i i i i f     → = =   . 积分和 被积函数 积分变量 被积表达式 面积元素

对二重积分定义的说明(1)在二重积分的定义中，对闭区域的划分是任意的。(2）当f(x,y)在闭区域上连续时，定义中和式的极限必存在，即二重积分必存在二重积分的儿何意义当被积函数大于零时，二重积分是柱体的体积当被积函数小于零时，二重积分是柱体的体积的负值

(1)在二重积分的定义中，对闭区域的划分是 任意的. (2) 当 f x y ( , )在闭区域上连续时，定义中和式 的极限必存在，即二重积分必存在. 对二重积分定义的说明： 二重积分的几何意义 当被积函数大于零时，二重积分是柱体的体积． 当被积函数小于零时，二重积分是柱体的体积的 负值．

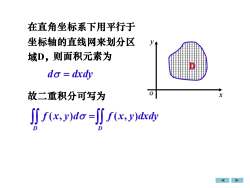
在直角坐标系下用平行于坐标轴的直线网来划分区N域D，则面积元素为Ddo = dxdy0x故二重积分可写为J f(x,y)do =JJ (x,y)dxdyD1

在直角坐标系下用平行于 坐标轴的直线网来划分区 域D， ( , ) ( , ) D D f x y d f x y dxdy  =   d dxdy  = 故二重积分可写为 x y o D 则面积元素为