《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-2 第二节 数量积、向量积、混合积

第二节数量积向量积*混合积两向量的数量积两向量的向量积向量的混合积1小结思考题
第二节 数量积 向量积 *混合积 ◼ 两向量的数量积 ◼ 两向量的向量积 ◼ *向量的混合积 ◼ 小结 思考题
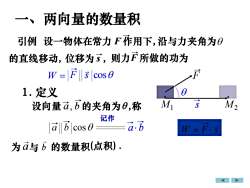
一、两向量的数量积引例 设一物体在常力 F作用下,沿与力夹角为的直线移动,位移为,则力F所做的功为FW =|F3|cos 001.定义3M2M设向量a,b的夹角为θ,称记作a.b[a/b cos 0W=F.3为α与b的数量积(点积)
一、两向量的数量积 M1 沿与力夹角为 的直线移动, W = 1. 定义 设向量 的夹角为 ,称 记作 的数量积(点积) . 引例 设一物体在常力 F 作用下, 位移为 s , 则力F 所做的功为 F s cos W F s = M2 a b a, b s 为 a 与 b

a.b=lalblcosoaIalcos =Prj,a: Ib Icos = Pr j,ba.b=ibiPrja=laPrj.b重要a.ba.bPrjb:Prj,a =1b1lal结论:两向量的数量积等于其中一个向量的模和另一个向量在这向量的方向上的投影的乘积.(两向量的数量积的几何意义)
a b a b | a || b | cos = | b | cos = | a | cos = 结论:两向量的数量积等于其中一个向量的 模和另一个向量在这向量的方向上的投影的 乘积. a b = a j ab = | | Pr 重要 | | Pr a a b j a b = j ba Pr j ab Pr (两向量的数量积的几何意义) b j ab Pr | | | | Pr b a b j ab =

a.b=lallblcos6数量积也称为“点积”或“内积”注对非零向量 a,b 有(1) 为锐角a·b>0;(2) 为钝角 台a.b<0.关于数量积的说明:(1) aa=ap.证:0=0,.a.a=laalcose=la?
数量积也称为 注 关于数量积的说明: | | . 2 a a a = = 0, aa = 证 “内积”. (1) (2) ab 0; a b 0. | a || a | cos = a b | a || b | cos = | | . 2 a (1) “点积”或 对非零向量 a b, 有 为锐角 为钝角

(2)a.b=0→ab.此时也称a与正交.证(→):a.b=0,la0,l0,元alb.0:.. cosO = 0,2'元:alb, ..0=():. cos0 = 0,2'a.b=lallblcoso= 0.例 i、、互相正交→i.=0,.=0k.i =0
() a b = 0, | a | 0, | b | 0, cos = 0, , 2 = a b. ⊥ () a b, ⊥ , 2 = cos = 0, a b =| a || b | cos = 0. 证 a b = 0 a b. ⊥ 此时也称 i j = 0, (2) a b 与 正交. 例 j k = 0, k i = 0. i、j、k 互相正交

2.数量积符合下列运算规律a.b=b.a(可用定义证)(1)交换律:(a+b).c=a.c+b.c(2)分配律:(3)若a为数:(aa)·b=a.(ab)=a(a.b)若 α μ为数:(aa)·(μub)=μu(a.b)(4)a.a=a.此外 a.a=0台a=0
2. 数量积符合下列运算规律 (1)交换律: a b b a = (2)分配律: a b c a c b c ( + ) = + (3)若 为数: a b = ( ) 若 、 为数: ( a)( b) = (可用定义证) (4) | | . 2 aa = a a = 0 a ( b) = (a b) (a b) 此外 a a = 0

之用向量的数量积,证明恒等式la++la-b=2la+2l即,平行四边形对角线的平方和等于四边的平方和(如图).-a+b证la+b+la-ba-ba=(a+ b)·(a+b)+(a-b).(a-b)=a.a+2a.b+b.b+a.a-2a.b+b.b= 2[a2 +2|b /
用向量的数量积,证明恒等式: 即,平行四边形对角线的平方和等于四边的平方 和(如图). 证 2 2 2 2 | a b | | a b | 2 | a | 2 | b | + + − = + 2 2 | a b | | a b | + + − (a b) (a b) (a b) (a b) = + + + − − a a a b b b a a a b b b = + 2 + + − 2 + 2 2 2 | a | 2 | b | = + a b a b + a b −

3.用坐标表示式计算数量积设a=ai+a,j+ak,b=bi+b,j+bka.b=(ai+a,j+a,k).(bi+b,j+b,k).iljlk.i.i=j.k=k.i=0分配律:i=l ik=1..i.i=i.i=k.k=la.b=a.b+a,b,+a,b数量积的坐标表达式
a a i a j a k, x y z = + + b bx i by j bzk 设 = + + a b = (a i a j a k) x y z + + (b i b j b k) x y z + + i j k ⊥ ⊥ i j = j k = k i = 0 | i |=| j |=| k |= 1 i i = j j = k k = 1 x x y y z z a b = a b + a b + a b 数量积的坐标表达式 3. 用坐标表示式计算数量积 分 配 律

4.两向量的夹角(数量积在几何中的应用)a.ba.b=alblcoso =→cos0[allb两向量夹角a.b,+a,b,+a,bcos =余弦的坐标+a,+a,b+b,+b表示式由此可知两向量垂直的充要条件为alb<←= a,bx +a,b, +a,b, =0数量积的物理意义为力F推动质点从点A沿直线运动到点B所作的功W=F×AB(即实例
a b | a || b | cos = | || | cos a b a b = 2 2 2 2 2 2 cos x y z x y z x x y y z z a a a b b b a b a b a b + + + + + + = 两向量夹角 余弦的坐标 表示式 a⊥b axbx + ayby + azbz = 0 由此可知两向量垂直的充要条件为 4. 两向量的夹角 (数量积在几何中的应用) 数量积的物理意义为 F 力 推动质点从点A 沿直线运动到点B所作的功 W F AB = (即实例)

例1 已知 a=(1,1,-4), b =(1,-2,2),求(1)a.b;(2)a与b的夹角;(3)a在b上的投影解 (1) a.b = 1·1+1.(-2)+(-4)·2 = -9.a,bx+a,b,+a,b,(2) cos =b?+b,?+bax+a,+a,13元~24a.b-3(3) a.b=biPrja :Prja1b1
解 a b ( 1 ) = 11+1(−2) + (−4) 2 = −9. (2) cos = , 21 = − . 43 = a b b j ab Pr (3) =| | 3. | | Pr = − = ba b j ab 例 1 求 2 2 2 2 2 2 x y z x y z x x y y z z a a a b b b a b a b a b + + + + + + 已知 a b = − = − (1,1, 4), (1, 2, 2), (1) ; a b (2) a 与 b 的夹角; (3) a 在 b 上的投影
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-5 第五节 曲面及其方程(surface).ppt
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-0 简介.ppt
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-3 第三节 平面及其方程.ppt
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-4 第四节 空间直线及其方程.ppt
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-6 第六节 空间曲线及其方程(space curve).ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-4 第四节 一阶线性微分方程.ppt
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-习题课.pptx
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-1 第一节 微分方程的基本概念.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-0 简介.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-5 第五节 可降阶的高阶微分方程.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-2 第二节 可分离变量微分方程.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-8 第八节 二阶常系数非齐次线性微分方程.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-3 第三节 齐次方程.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-6 第六节 高阶线性微分方程.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-7 第七节 常系数齐次线性微分方程.ppt
- 《高等数学》课程教学资源(PPT课件)第六章 定积分的应用 6-2 第二节 定积分在几何学上的应用.ppt
- 《高等数学》课程教学资源(PPT课件)第七章 微分方程 7-习题课.ppt
- 《高等数学》课程教学资源(PPT课件)第五章 定积分 5-1 第一节 定积分的概念与性质.ppt
- 《高等数学》课程教学资源(PPT课件)第六章 定积分的应用 6-0 简介.ppt
- 《高等数学》课程教学资源(PPT课件)第六章 定积分的应用 6-1 第一节 定积分的元素法.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-习题课.ppt
- 《高等数学》课程教学资源(PPT课件)第八章 向量代数与空间解析几何 8-1 第一节 向量及其线性运算.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-7 第七节 方向导数与梯度.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-8 第八节 多元函数的极值与拉格朗日乘数法.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-3 第三节 全微分.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-4 第四节 多元复合函数的求导法则.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-6 第六节 多元函数微分学的几何应用.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-0 简介.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-5 第五节 隐函数的求导公式(implicit function).ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-2 第二节 偏导数.ppt
- 《高等数学》课程教学资源(PPT课件)第九章 多元函数微分法及其应用 9-1 第一节 多元函数的基本概念.ppt
- 《高等数学》课程教学资源(PPT课件)第十章 重积分 10-习题课.ppt
- 《高等数学》课程教学资源(PPT课件)第十章 重积分 10-04 第四节 重积分的应用.ppt
- 《高等数学》课程教学资源(PPT课件)第十章 重积分 10-0 简介.ppt
- 《高等数学》课程教学资源(PPT课件)第十章 重积分 10-03 第三节 三重积分.ppt
- 《高等数学》课程教学资源(PPT课件)第十章 重积分 10-01 第一节 二重积分的概念与性质.ppt
- 《高等数学》课程教学资源(PPT课件)第十一章 曲线曲面积分 11-习题课.ppt
- 《高等数学》课程教学资源(PPT课件)第十一章 曲线曲面积分 11-07 第七节 斯托克斯公式、环流量与旋度.ppt
- 《高等数学》课程教学资源(PPT课件)第十一章 曲线曲面积分 11-05 第五节 对坐标的曲面积分(surface integral).ppt
- 《高等数学》课程教学资源(PPT课件)第十一章 曲线曲面积分 11-06 第六节 高斯公式、通量与散度.ppt
