《高等数学》课程教学资源（PPT课件）第十一章 曲线曲面积分 11-03 第三节 格林公式及其应用

第三节格林公式及其应用区域连通性的分类格林公式平面上曲线积分与路径无关的等价条件小结思考题

第三节 格林公式及其应用 ◼ 区域连通性的分类 ◼ 格林公式 ◼ 平面上曲线积分与路径无关的等价条件 ◼ 小结 思考题

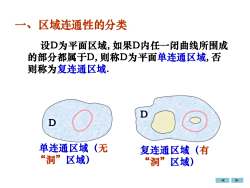
区域连通性的分类设D为平面区域，如果D内任一闭曲线所围成的部分都属于D，则称D为平面单连通区域，否则称为复连通区域DD(无单连通区域（有复连通区域“洞”区域)“洞”区域)

一、区域连通性的分类 设D为平面区域, 如果D内任一闭曲线所围成 的部分都属于D, 则称D为平面单连通区域, 否 则称为复连通区域. 复连通区域（有 “洞”区域） 单连通区域（无 “洞”区域） D D

二、1.格林公式定理1设区域D是由分段光滑正向曲线L围成函数 P(x,y),Q(x,)在D上具有连续一阶偏导数则有apdxdy = Φ Pdx + QdyaxayD-（格林公式）或aaaxaydxdy=ΦPdx+Qdy.PQD1

定理1 设区域D是由分段光滑正向曲线L围成, 则有 d d d d D L Q P x y P x Q y x y     − = +         ( 格林公式 ) 函数 在D上具有连续一阶偏导数, d d d d x y D L x y P x Q y P Q     = +   或 二、1. 格林公式

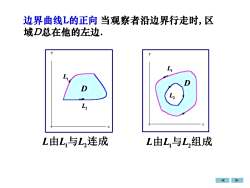
当观察者沿边界行走时，区边界曲线L的正向D总在他的左边/DL由L,与L,连成L由L,与L,组成

L由L1与L2连成 L由L1与L2组成 边界曲线L的正向 当观察者沿边界行走时, 区 域D总在他的左边. L2 D L1 L2 L1 D

证明(1)V若区域D既是X一型文是xE=Y一型,即平行于坐标轴 x=y(y)DB的直线和L至多交于两x+y,(y)点.SCy= Pi(x)xbCD=((x, y)(x)≤y≤P2(x),a≤x≤b)D=((x, y)y(y)≤x≤y2(y),c≤ y≤d)

{( , ) ( ) ( ), } D = x y 1 x  y  2 x a  x  b 证明(1) 若区域D既是X − 型又是 Y − 型,即平行于坐标轴 的直线和L至多交于两 点. {( , ) ( ) ( ), } D = x y 1 y  x  2 y c  y  d y x o a b D cd ( ) y = 1 x ( ) y =  2 x A B C E ( ) 2 x =  y ( ) 1 x =  y

2(y)00aQTdxdy = ["XoxJyi(y)ax0= f" Q(y2(y), y)dy - f" (vi(y), y)dy1EQ(x, y)dy - Jcur Q(x, y)dydCBDx=yyon-Q(x, y)dy + feic Q(x, y)dyCRE2x =,(y)C*xf,Q(x, y)dyolapdxdy = , P(x, y)dx同理可证ayD

dx xQ dxdy dy xQ yy dc D     =  ( ) ( ) 21    = − dc dc Q( ( y), y)dy Q( ( y), y)dy  2  1   = − CBE CAE Q(x, y)dy Q(x, y)dy   = + CBE EAC Q(x, y)dy Q(x, y)dy  = L Q ( x, y )dy 同理可证   =  − L D dxdy P x y dx yP ( , ) y x od ( ) 2 x =  y D c CE ( ) 1 x =  y

两式相加得apaq[[Pdx + Qdydxdy=ayaxD证明(2)L,DD2若区域D由按段光滑的闭曲线围成.如图，DD,L将D分成三个既是X一型又是Y-型的区域D,,Dz,D3apapaQaQdxddxdiaxaxayayDD,+D2+D3

若区域D由按段光滑 的闭曲线围成.如图, 证明(2) L L1 L2 L3 D D 1 D 2 D 3 两式相加得 ( ) L D Q P dxdy Pdx Qdy x y   − = +     将D分成三个既是X −型又是 Y −型的区域D1 ,D2 ,D3 .   + +  −  =  −  1 2 3 ( ) ( ) D D D D dxdy yP xQ dxdy yP xQ

apapaqapaQaQ叮dxddxdydxdayaxayayaxaxD2DiD3Pdx +Qdy +Pdx +Qdy +Pdx +Qdy$, Pdx + Qdy(L,L,,L， 对D来说是为正方向)D

     −   +   −   +   −   1 2 3 ( ) ( ) ( ) D D D dxdy y P x Q dxdy y P x Q dxdy y P x Q    = + + + + + L1 L2 L3 Pdx Qdy Pdx Qdy Pdx Qdy  = + L Pdx Qdy D1 D2 D3 L L1 L2 L3 1, 2 3 ( , L L L 对D来说是为正方向）

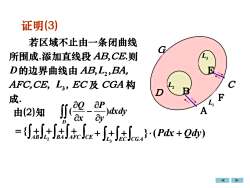
证明(3)若区域不止由一条闭曲线7所围成.添加直线段AB,CE.则ED的边界曲线由 AB,L2,BA,CAFC,CE,L，EC及 CGA构BDF成.L,apQA)dxdy由(2)知d=(JtJ+JaJt Jce+ J+JJeca} (Pdx + Qdy)

G D L 3 L 2 F C E L1 A B 证明(3) 若区域不止由一条闭曲线 所围成.添加直线段 AB,CE.则 D的边界曲线由 AB,L2,BA, AFC,CE, L 3, EC 及 CGA 构 成. 由(2) 知 ( ) D Q P dxdy x y   −         = + + + + AB L 2 BA AFC CE {    + + +  + L EC CGA} (Pdx Qdy) 3

(f, + f, + fL(Pdx + Qdy)$, Pdx + Qdy(L,Lz,L,对D来说为正方向)沟通了沿闭曲线的积分与格林公式的实质：二重积分之间的联系，便于记忆形式aa门ayldxdy = , Pdx + Qdy.axDPQ

 = + L Pdx Qdy    = + + + 2 3 1 ( )( ) L L L Pdx Qdy ( , ) L1, L2 L3对D来说为正方向 便于记忆形式:    = +    L D dxdy Pdx Qdy P Q x y . 格林公式的实质: 沟通了沿闭曲线的积分与 二重积分之间的联系