《高等数学》课程教学资源（PPT课件）第六章 定积分的应用 6-习题课

第六章习题课一、主要内容二、典型例题

第六章 习题课 一、主要内容 二、典型例题 1

主要内容理论依据名称释译微元法的所特求点量解题步骤定积分应用中的常用公式

微 元 法 理 论 依 据 名 称 释 译 所 求 量 的 特 点 解 题 步 骤 定积分应用中的常用公式 一、主要内容 2

1、理论依据设f(x)在[a,b]上连续,则它的变上限积分U(x) = ( f(t)dt(1)是 f(x)的一个原函数,即 dU(x)= f(x)dx,于是(2)f(x)dxdU =UY这表明连续函数的定积分就是（1)的微分的定积分。3

1、理论依据 . (1) ( ) (2) ( ) , ( ) ( ) , ( ) ( ) (1) ( ) [ , ] , 定积分 这表明连续函数的定积分就是 的微分的 于是 是 的一个原函数 即 设 在 上连续 则它的变上限积分 f x dx dU U f x dU x f x dx U x f t dt f x a b b a b a x a = = = =    3

2、名称释译由理论依据(2)知,所求总量A就是其微分dU=f(x)dx从a到b的无限积累(积分):U = ("f(x)dx这种取微元f(x)dx计算积分或原函数的方法称微元法

2、名称释译 . ( ) ( ) ( ) ( ): (2) , 方法称微元法 这种取微元 计算积分或原函数的 从 到 的无限积累 积分 由理论依据 知 所求总量 就是其微分 f x dx U f x dx dU f x dx a b A b a = = 4

3、所求量的特点(1）U是与一个变量x 的变化区间a,b|有关的量；（2）U对于区间a,b具有可加性，就是说，如果把区间a,b分成许多部分区间，则U相应地分成许多部分量，而U等于所有部分量之和；（3）部分量△U,的近似值可表示为f（)△x;；就可以考虑用定积分来表达这个量U

（1）U 是与一个变量x 的变化区间a,b 有关 的量； （2）U 对于区间a,b具有可加性，就是 说，如果把区间a,b分成许多部分区间，则 U 相应地分成许多部分量，而U 等于所有部 分量之和； （3）部分量Ui的近似值可表示为 i xi f ( ) ； 就可以考虑用定积分来表达这个量U. 3、所求量的特点 5

4、解题步骤1)根据问题的具体情况，选取一个变量例如x为积分变量，并确定它的变化区间[a,b];2）设想把区间[a,bl分成n个小区间，取其中任一小区间并记为[x,x+dx]，求出相应于这小区间的部分量△AU的近似值．如果AU能近似地表示为[a,bl上的一个连续函数在x处的值f(x)与dx的乘积，就把f(x)dx称为量U的元素且记作dU， 即dU = f(x)dx;3）以所求量U的元素f(x)dx为被积表达式，在区间[a,b]上作定积分，得U=f(x)dx即为所求量U

1)根据问题的具体情况，选取一个变量例如x 为 积分变量，并确定它的变化区间[a,b]； 2）设想把区间[a,b]分成 n 个小区间，取其中任 一小区间并记为[x, x + dx]，求出相应于这小区 间的部分量U的近似值．如果U 能近似地表 示为[a,b]上的一个连续函数在x处的值 f (x)与 dx的乘积，就把 f (x)dx称为量U 的元素且记 作dU，即 dU = f (x)dx ； 3）以所求量U 的元素 f (x)dx为被积表达式，在 区间[a,b]上作定积分，得 =  b a U f (x)dx， 即为所求量U ． 4、解题步骤 6

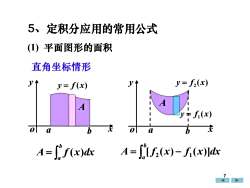
5、定积分应用的常用公式(1)平面图形的面积直角坐标情形y= f,(x)y1y= f(x)Afi(x)V丰1-txo1obbaa["f(x)dx(If2(x) - f(x)]dx

5、定积分应用的常用公式 (1) 平面图形的面积 x y o y = f (x) =  b a A f (x)dx x y o ( ) y = f 1 x ( ) y = f 2 x =  − b a A [ f2 (x) f1 (x)]dx A A 直角坐标情形 a b a b 7

参数方程所表示的函数x = p(t)如果曲边梯形的曲边为参数方程y=y(t)曲边梯形的面积 A=y(t)p'(t)dt（其中t,和t,对应曲线起点与终点的参数值）在[t,t,]（或[t2,t]）上x=β(t)具有连续导数y=y(t)连续

如果曲边梯形的曲边为参数方程    = = ( ) ( ) y t x t   曲边梯形的面积  =  2 1 ( ) ( ) t t A  t  t dt （其中 1 t 和 2 t 对应曲线起点与终点的参数值） 在[ 1 t , 2 t ]（ 或[ 2 t , 1 t ]） 上x = (t)具有连续导数， y =(t)连续. 参数方程所表示的函数 8

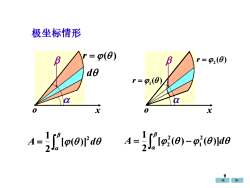
极坐标情形= β(0)Br = Φ2(0)3der = Φ(0)αa0x0x" [2(0) -(0)]d0[p()]'d12Ja9

 =   A   d 2 [ ( )] 2 1 o x  d  r = ( )   o x ( ) r =  2  ( ) r = 1   = −   A [ ( )  ( )]d 2 1 2 1 2 2 极坐标情形 9

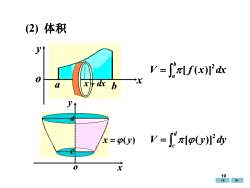
(2) 体积yt (. 元[f(x)] dx0xxdxbaV[p(y)]’ dyx =p(y)0x10

(2) 体积 x x + dx x y o V f x dx b a 2 [ ( )] =   V y dy d c 2 [( )] =  x y o x = ( y) c d 10