《高等数学》课程教学资源（PPT课件）第四章 不定积分 4-4 第四节 有理函数的积分

第四节有理函数的积分有理函数的积分可化为有理函数的积分举例小结思考题

第四节 有理函数的积分 ◼ 有理函数的积分 ◼ 可化为有理函数的积分举例 ◼ 小结 思考题

基本积分法：直接积分法：换元积分法：分部积分法求导初等函数初等函数积分例如，下列函数积分都不是初等函数sinxdx, J sinx'dx, JdxdxInxXdx[ /1+x3 dx, [ /1-k’ sin’ xdx (0<k<1)+在概率论、数论、光学、傅里叶分析等领域的范围有重要应用的积分,都属于“积不出

基本积分法: 换元积分法; 分部积分法 初等函数 求导 初等函数 积分 例如,下列函数积分都不是初等函数 d , 2 e x x  − d , sin x x x  sin d , 2 x x  d , ln 1 x x  , 1 d  4 + x x 1 d , 3  + x x 1 sin d (0 1) 2 2 −    k x x k 直接积分法;  在概率论、数论、光学、傅里叶分析等领域 有重要应用的积分,都属于“积不出”的范围

有理函数的积分有理函数的定义两个多项式的商表示的函数称之+axn-1 +... +a,P(x)ax+b xm-1+... +b.Q(x)box2其中m、n都是非负整数ao,ai,..an及bo,b,,..bm都是实数且a,≠0,b,0假定分子与分母之间没有公因式(1)n<m,真分式；(2)n≥m,假分式

其中m、n都是非负整数; , , , , , a0 a1 an 及b0 b1 bm 都是实数 0, 0. 且a0  b0  一、有理函数的积分 假定分子与分母之间没有公因式 (1) n  m, 真分式; (2) n  m, 假分式. 有理函数的定义 两个多项式的商表示的函数称之. = ( ) ( ) Q x P x n n n a x +a x + +a -1 0 1 m m m b x +b x +b -1 0 1 +

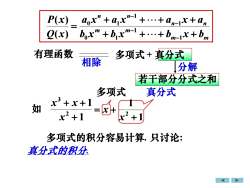
P(x)a,x" +axn-I +..+an--x+a,b,xm +b,xm-1 +.+bm-x+bQ(x)有理函数多项式+真分式相除分解若干部分分式之和多项式真分式x+x+1如xx2+1x-+1多项式的积分容易计算.只讨论：真分式的积分

如 1 1 2 3 + + + x x x 1 1 2 + = + x x m m m m n n n n b x b x b x b a x a x a x a Q x P x + + + + + + + + = − − − − 1 1 0 1 1 1 0 1 ( ) ( )   多项式的积分容易计算. 真分式的积分. 只讨论: 多项式 真分式 有理函数 相除 多项式 + 真分式 分解 若干部分分式之和

对一般有理真分式的积分，代数学中下述定理起着关键性的作用P(x)定理均可表为有限个任何有理真分式Q(x)部分分式的和如果分母多项式Q(x)在实数域上的质因式分解式为Q(x) = b,(x -a)~ ...(x2 + px +q)" ..., (p2 - 4q<0)P(x).则几,μ为正整数可唯一的分解为Q(x)

对一般有理真分式的积分,代数学中下述定 理起着关键性的作用. 定理 任何有理真分式 均可表为有限个 ( ) ( ) Q x P x 部分分式的和.如果分母多项式Q(x)在实数域 上的质因式分解式为: ( ) ( ) ( ) , 2 Q x = b0 x − a   x + px + q   : ( ) ( ) 则 可唯一的分解为 Q x P x ,为正整数, ( 4 0) 2 p − q 

Q(x) = b. (x-a).(x2 + px + q)".. (p2 - 4q < 0)2个常数待定P(x)A2一Q(x)ax一ax-Mx+NM.x+N+(x? + px+g)u-+ +(x2 + px+g) uM.x+N2u个常数待定?x+px+q其中诸A,M,,N,都是常数可由待定系数法确定P(x)的部分分式(最简分式)式中每个分式叫做Q(x)

= ( ) ( ) Q x P x 其中诸 , , 都是常数, Ai Mi Ni 可由待定系数法确定, 式中每个分式叫做 的 ( ) ( ) Q x P x + ( − ) 1 x a A 部分分式(最简分式). ( ) ( ) ( ) , 2 Q x = b0 x − a   x + px + q   ( 4 0) 2 p − q  + ( − ) 2 x a A + x − a + + + + + 2 −1 2 2 ( )  x px q M x N + + + + + + x px q M x N 2      −1 A 1 ( ) + ( + + ) 2 x px q  M1 x + N1 个常数待定 2个常数待定

用此定理有理函数的积分就易计算了耳由下面的例题可看出：有理函数的积分是初等函数注系数的确定，一般有三种方法(1)等式两边同次幂系数相等：(2) 赋值;(3)求导与赋值结合使用

用此定理有理函数的积分就易计算了. 且由下面的例题可看出: 有理函数的积分是初等函数. 注 系数的确定,一般有三种方法: (1) 等式两边同次幂系数相等; (2) 赋值; (3) 求导与赋值结合使用

假分式x+x+例1 求dxx2 +1解由多项式除法，有x3+x+11=x+x? +1x? +12dx原式={xdx++ arctan x + C2+1说明：当被积函数是假分式时,应把它分为个多项式和一个真分式，分别积分

例1 求 x x x x d 1 1 2 3  + + + 解 由多项式除法,有 = + + + 1 1 2 3 x x x   + = + 1 d d 2 x x 原式 x x x C x = + arctan + 2 2 说明:当被积函数是假分式时,应把它分为 一个多项式和一个真分式,分别积分. 1 1 2 + + x x 假分式

x+3例2 求dx.22-5x+6xABx+3x+3解x-3x-5x+6x-2(x -2)(x-3)因式分解 x+3= A(x-3)+ B(x-2)x+3=(A+B)x-(3A+2B)比较系数A+B=1A=-5B=6-(3A+2B)=3,6-5x+3x2-5x+6x-2x-3

 − + + x x x x d 5 6 3 例 2 2 求 5 6 3 2 − + + x x x ( 2)( 3 ) 3 − − + = x x x + − = x 2 A x + 3 = A ( x − 3 ) + B ( x − 2 ) x + 3 = ( A + B ) x − ( 3 A + 2 B ) − + = + =  (3 2 ) 3, 1, A B A B  == −  6 5 BA 5 6 3 2 − + +  x x x 解 3 6 25 − + −− = x x x − 3 B 比较系数 因式分解

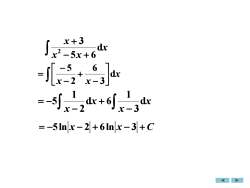
x+3dx25x +656dx2Xdxdxx-2x-3= -5ln|x -2|+6lnx-3+C

 − + + x x x x d 5 6 3 2   − + − = − x x x x d 3 1 d 6 2 1 5 x x x d 3 6 2 5        − + − − = = −5ln x − 2 + 6ln x − 3 + C