《高等数学》课程教学资源（PPT课件）第一章 函数与极限 1-03 第三节 函数的极限

第三节函数的极限函数极限的定义函数极限的性质■小结思考题

第三节 函数的极限 ◼ 函数极限的定义 ◼ 函数极限的性质 ◼ 小结 思考题

函数极限的定义1.函数在无穷远点的极限设对充分大的x，函数f(x)处处有定义如果随着x的无限增大,相应的函数,f(x)就无限接近某一常数A.由此可引入函数在无穷远处的极限概念x趋向于正无穷x→+8x趋向于负无穷x→-0x趋向于无穷x→8表示x,一x,lx无限增大的过程

1.函数在无穷远点的极限 设对充分大的x, 函数 f ( x) 处处有定义. 如果随着x的无限增大,相应的函数 f ( x) 就 无限接近某一常数 A. 由此可引入函数在无 穷远处的极限概念. x → + x → − x →  表示 − x, 无限增大的过程. x 趋向于负无穷   x 趋向于无穷    x 趋向于正无穷 x, | x | 一、函数极限的定义

函数极限的定义1.自变量趋于有限值时函数的极限考虑x→xo 时函数极限的定义测量正方形面积.(真值：边长为xo;面积为A）引例直接观测值确定直接观测值精度S：边长xx-xo<任给精度ε,要求x2-A间接观测值面积 x2

一、函数极限的定义 1.自变量趋于有限值时函数的极限 考虑 时函数极限的定义 引例 测量正方形面积. (真值: 边长为 面积为A ) 边长 面积 直接观测值 间接观测值 任给精度  , 要求 x − A   2 确定直接观测值精度  : x − x0  

定义1（ε-）设函数f(x)在点xo某去心邻域内有定义.若>0,>0,使当0x-xl时,恒有f(x)-A0,3S>0,当 xU(xo,S)x→>xo时,有|f(x)-A<8

若  0, 定义1 ( −  ) 设函数 有定义.   0, 0 , 使当  x − x0  时 f (x) − A   ( ) , 则称x → x0 时函数f x 有极限A lim ( ) , 0 f x A x x = → 记作 ( ) ( ). x A x x0 或 f → → 恒有 f (x) 在点x0某去心邻域内 即 当 时, 有

注(1)定义中的 0<x-x表示x≠xo所以x →x,时,f(x)有没有极限与f(x)在点xo是否有定义并无关系(2)定义中S标志x接近xo的程度,它与8有关.一般地说，6越小，也将越小，(3)不要求最大的S，只要求S存在即可

注 (1) 定义中的 0  x − x0 所以 , x → x0时 f (x)有没有极限与f (x)在点x0 是否有定义并无关系. (2) 定义中  标志 x 接近 x0 的程度,  也将越小. (3) 不要求最大的  , , 表示 x  x0 它与  一般地说,  越小, 只要求  存在即可. 有关

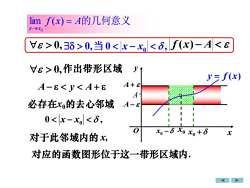
lim f(x)= A的几何意义X-→XoV>0,3>0,当00,作出带形区域yy= f(x)A+A-8<Y<A+8A-必存在x的去心邻域A-8--0<x-x|<,-110X- Xo x+8x对于此邻域内的x对应的函数图形位于这一带形区域内

  0, A−   y  A+  必存在x0的去心邻域 0 ,  x − x0   对于此邻域内的 x, 对应的函数图形位于这一带形区域内. f x A的几何意义 x x = → lim ( ) 0 作出带形区域   0, 0 ,   0,当  x − x0   f (x) − A   x y O y = f (x) A−  A+  x0 −  x0 x0 +  A

-般说来,论证lim f(x)=A,应从不等式f(x)-A<ε出发,推导出应小于怎样的正数这个正数就是要找的与8相对应的S，找到S就证明完毕.这个推导常常是困难的但是，注意到我们不需要找最大的S，所以可把 f(x)-A适当放大些,变成易于解出x一x.的式子,找到一个需要的s

一般说来, lim ( ) , 0 f x A x x = → 论证 应从不等式 f (x) − A   出发, 推导出应小于怎样的正数, 这个正数就是要找的与  相对应的  , 这个推导常常是困难的. 但是, 注意到我们不需要找最大的  , 所以 f (x) − A 适当放大些, 的式子, 变成易于解出 x − x0 找到一个需要的  . 找到  就证明完毕. 可把

例1.证明lim C=C（C为常数）x-→>xof(x)-A|=|C-C|=0证：故>0,对任意的>0,当0xo

例1. 证明 证: f (x) − A 故   0, 对任意的   0, 当 时 , 因此 总有

lim(2 x -1) = 1例2.证明x-1证 [f(x)-A| =|(2x-1)-1| =2|x-1]>0,欲使|(x)-A|1

例2. 证明 证 = 2 x −1   0, 欲使 取 , 2   = 则当 0  x −1   时 , 必有 因此 只要

例3 证明limx-→1证 函数在点x=1 处没有定义，x-1- 2=x-: f(x)-A:x-1>0,要使|f(x)A<ε，只要取=,当0<x-1<8时,有<8.x-1X:2limx-1x-→1

例3 2. 1 1 lim 2 1 = − − → x x x 证明 证 2 1 1 ( ) 2 − − − − = x x  f x A   0, 只要取 =  , 当0  x −1  时, 函数在点 = x − 1 f (x) − A   , 2 , 1 1 2 −   − − x x 有 2. 1 1 lim 2 1 = − −  → x x x x = 1 处没有定义. 要使