《高等数学》课程教学资源（PPT课件）第二章 导数与微分 2-03 第三节 高阶导数

第三节高阶导数高阶导数的定义儿个基本初等函数的n阶导数莱布尼茨(Leibniz)公式小结思考题

◼ 高阶导数的定义 ◼ 莱布尼茨(Leibniz)公式 ◼ 小结 思考题 ◼ 几个基本初等函数的n阶导数 第三节 高阶导数

高阶导数也是由实高阶导数的定义一际需要而引入的问题：变速直线运动的加速度设 s = s(t),则瞬时速度为v(t)= s'(t)：加速度a是速度对时间的变化率这就是二阶导数的物理意义.. a(t) = v'(t)=[s'(t)]定义 如果函数f(x)的导数f'(x)在点x处可导,即f(x+ △x) - f(x)(f'(x))= limAxAr-→0存在,则称(f'(x)为函数f(x)在点x处的二阶导数,dyd'f(x)或记作 f"(x),J",dx?dx

问题:变速直线运动的加速度. 设 s = s(t),则瞬时速度为v(t) = s(t) 加速度a是 a(t) = 定义 如果函数f ( x)的导数f ( x) x f x x f x f x x  +  −  =  → ( ) ( ) ( ) lim 0 高阶导数也是由实 际需要而引入的. v(t) = [s (t)] 这就是二阶导数的物理意义 速度v对时间t的变化率 一、高阶导数的定义 ' 存在, 则称( f ( x))为函数f ( x)在点x处的 二阶导数. ( ) ' ' 在点x处可导,即 记作 f ( x), 2 2 d d x y . d d ( ) 2 2 x f x y  , 或

二阶导数的导数称为三阶导数,f"(x)，y"三阶导数的导数称为四阶导数,(4)(x)，j(),dx一般地，函数f(x)的n-1阶导数的导数称为函数f(x)的n阶导数,记作dnd" f(x)f(n)(x), y(n)或dr"dx二阶和二阶以上的导数统称为高阶导数相应地,f(x)称为零阶导数f(x)称为一阶导数

函 数f ( x)的n − 1阶导数的导数称为 . d d ( ) d d ( ), , ( ) ( ) n n n n n n x f x x y f x y 或 三阶导数的导数称为 二阶和二阶以上的导数统称为 相应地, f (x)称为零阶导数; . d d ( ), , 3 3 x y 二阶导数的导数称为 f  x y  . d d ( ), , 4 4 (4) (4) x y f x y 高阶导数. f (x)称为一阶导数. 函数f ( x)的 三阶导数, 四阶导数, n阶导数, 记作 一般地

由高阶导数的定义，欲求函数的高阶导数只需按求导法则和基本公式一阶阶的算下去而不需要新的方法例1设y=arctanx,求y"09x=012x解J'(1+x")1+x2(3x2 - 1)-2x(1 + x°)3(1+ x2)22(3x2 -1)-2x= 0; J=-2.=0(1+x")(1+ x")3x=0x=0

例1 解 2 1 1 x y +  = ) 1 1 ( 2  +  = x y 2 2 (1 ) 2 x x + − =        + −  = 2 2 (1 ) 2 x x y 2 3 2 (1 ) 2(3 1) x x + − = = 0; = −2. 由高阶导数的定义,欲求函数的高阶导数, 只需按求导法则和基本公式一阶阶的算下去, 而不需要新的方法. arctan , , . =0 =0 =   x x 设 y x 求y y 0 0 2 2 (1 ) 2 = = + −   = x x x x y 0 2 3 2 0 (1 ) 2(3 1) = = + −  = x x x x y

二、几个基本初等函数的n阶导数例2 设 y= x~ (α R),求y(n),解 j'= oxα-1j" = (axa-l)'= α(α -1)xα-2j" = (α(α- 1)xα-2) = α(α -1)(α- 2)xα-3y(n) = α(α-1)..(α - n + 1)xaα-n(n ≥ 1)若α为自然数n,则y(n) = (x")(")= n!,(n+I) = (n!)' = 0

例2 ( ), . (n) 设 y = x   R 求y  解 −1  =  y x ( ) 1  =  − y x 2 ( 1) − = −    x  3 ( 1)( 2) − = − −  ( ( 1) )    x 2  = −  − y   x ( 1) ( 1) ( 1) ( ) = − − +  − y n x n n  n     若 为自然数n, ( ) ( ) ( ) n n n y = x = n!, ( !) ( 1) =  + y n n = 0. 则 二、几个基本初等函数的n阶导数

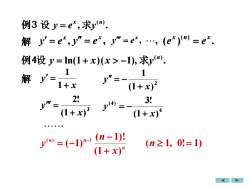
例3 设 =e*,求y(n),解 y'=e*,y"=e*, y" =e",..,(e*)(n) =e*例4设 y = In(1 +x)(x >-1),求y(n),11解 131+x(1 + x)2!3!D（4)(1 + x)(1 +x)4J(") =(-1)-i (n -1)!(n ≥1, 0!=1)(1 +x)

例 3 , . x (n) 设 y = e 求y 解 , x y  = e , x y  = e ,  , x y  = e ( ) . x (n) x e = e 例 4 ln(1 )( 1), . (n) 设 y = + x x  − 求y 解 x y +  = 1 1 2 (1 ) 1x y +  = − 3 (1 ) 2!x y +  = 4 (4) (1 ) 3!x y + = − ( 1, 0! 1) (1 ) ( 1)! ( 1) ( ) 1  = +− = − − n x n y n n n 

例5 设= sin x,求y(n)T解 J'=cosx = sin(x+π2元元T儿sin(x + 2.y" = cos(x + sin(x +2222元元sin(x + 3.y" = cos(x + 2.22元元y(n) = sin(x+n.即 (sinx)(n) = sin(x + n :22元同理可得(cosx)(")= cos(x+ n.2

例5 sin , . (n) 设 y = x 求y 解 y = cos x ) 2 sin(  = x + ) 2 cos(  y = x + ) 2 2 sin(  +  = x + ) 2 sin( 2  = x +  ) 2 cos( 2  y = x +  ) 2 sin( 3  = x +   ) 2 sin( ( )  y = x + n n ) 2 (cos ) cos( ( )  x = x + n  同理可得 n 即 ) 2 (sin ) sin( ( )  x = x + n n

注求n阶导数时，关键要寻找规律一般求至三阶，便可看出规律；另外在求导过程中不要急于合并，分析结果的规律性,写出n阶导数

注 求n阶导数时, 关键要寻找规律, 另外在 的规律性,写出n 阶导数. 一般求至三阶,便可看出规律; 求导过程中不要急于合并, 分析结果

1求y(n)例6 J=x2-3x+2111解y=x-3x+2x-2x-11-1-111)(x - 2)2(x-1)1.21.2(-1)(-2)(-1)(-2)(-1)1(x-2)(x -1)3(x-2)(x-1)n!n!(-1)(x- 2)n+I(x -1)n+111=(-1)" n!(x -1)n+1+-2)n

例6 , . 3 2 1 ( ) 2 n y x x y 求 − + = 解 3 2 1 2 − + = x x y ( ) ( ) 3 3 1 ( 1)( 2) 2 ( 1)( 2) − − − − − − −  = x x y 2 2 ( 1) 1 ( 1) ( 2) 1 ( 1) − − − − = − x x 3 2 3 2 ( 1) 1 2 ( 1) ( 2) 1 2 ( 1) −  − − −  = − x x  1 1 ( ) ( 1) ! ( 1) ( 2) ! ( 1) + + − − − − = − n n n n n x n x n y       − − − = − +1 +1 ( 1) 1 ( 2) 1 ( 1) ! n n n x x n 1 1 2 1 − − − = x x 2 2 ( 1) 1 ( 2) 1 − − − − −  = x x y

求n阶导数需要运用技巧（通过四则运算变量代换，恒等变形尽可能化为求某些熟知函数的n阶导数公式，使问题简化几个常用高阶导数公式(e*)(n) =e*(1)(a*)(n) =a*.ln" a (a>0)元(2) (sin kx)(n) = k" sin(kx + n . "2元(3) (cos kx)(n) = k" cos(kx + n . "2(4)(x)(") = α(α -1) (α - n+ 1)xα-n1)(n)n!(5) (ln x)(") =(-1)"-1 (n-1)-1tnix

求n阶导数需要运用技巧 几个常用高阶导数公式 n n x n x − = − − +   (4) ( ) ( 1) ( 1) ( )  n n n x n x ( 1)! (5) (ln ) ( 1) ( ) 1 − = − − ) 2 (2) (sin ) sin( ( )  kx = k kx + n n n ) 2 (3) (cos ) cos( ( )  kx = k kx + n n n (1) ( ) ln ( 0) ( ) a = a  a a  x n x n x n x e = e ( ) ( ) 1 ( ) ! ( 1) 1 +  = −      n n n x n x 函数的n阶导数公式,使问题简化. 尽可能化为求某些熟知 (通过四则运算, 变量代换,恒等变形)