《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用 3-01 第一节 微分中值定理

第一节微分中值定理罗尔定理拉格朗中值定理柯西中值定理1小结吉思考题

◼ 罗尔定理 ◼ 拉格朗日中值定理 ◼ 柯西中值定理 ◼ 小结 思考题 第一节 微分中值定理

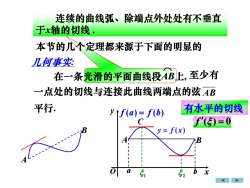
连续的曲线弧、除端点外处处有不垂直于x轴的切线本节的儿个定理都来源于下面的明显的几何事实光滑的平面曲线段AB上，至少有在一条一点处的切线与连接此曲线两端点的弦AB平行.有水平的切线y tf(a) = f(b)f'()=0中Sy= f(x)BY-可ab52Six

本节的几个定理都来源于下面的明显的 AB 在一条光滑的平面曲线段AB上, ⌒ 至少有 与连接此曲线两端点的弦 平行. 几何事实: 一点处的切线 连续的曲线弧、除端点外处处有不垂直 于x轴的切线 . 有水平的切线 f ( ) = 0 A B x y O y = f ( x)  1  2 A B a b C f (a) = f (b)

罗尔Rolle.(法)1652-1719一、罗尔(Rolle)定理罗尔定理若函数f(x)满足:(1)在闭区间a,bl上连续(2)在开区间(a,b)内可导(3) f(a) = f(b)则在开区间(a,b)内至少存在一点,使得f'()= 0.如, f(x)=x2 -2x -3=(x - 3)(x +1)在[-1,3]上连续,在(-1,3)内可导,且 f(-1)= f(3)= 0,f(x)=2(x-1),取 =1,(1 e (-1,3) f'()= 0

罗尔定理 若函数f (x)满足: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) f (a) = f (b), 罗尔 Rolle,(法)1652-1719 则在开区间(a,b)内至少存在一点, 使得 f ( ) = 0. 如, ( ) 2 3 2 f x = x − x − = (x − 3)(x + 1). 在[−1,3]上连续,在(−1,3)内可导,且 f (−1) = f (3) = 0, f (x) = 2(x −1),取 = 1, (1(−1,3)) 一、罗尔(Rolle)定理 f ( ) = 0

费马Fermat,(法）1601-1665费马引理设函数f(x)在点x的某邻域U(x)内有定义，且f(x)存在,如果对VxU(x),有f(x)≤ f(xo)(或f(x) ≥ f(xo))那么f'(x)=0.分析 由于f()存在,则 f(x)在x=x的左导数f'(x)和右导数f(xo)存在 且相等,即f'(x)= f'(x)= f(xo)然后利用f'(x)和f(xo）的符号证得f"(x）=0

费马引理 费马 Fermat,(法) 1601-1665 有定义, 如果对 ( ), x U x0 有 ( ) ( ) x0 f x  f ( ( ) ( )), x0 或f x  f ( ) 0. 那么 f  x0 = 分析 ( ) ( ) ( ) 0 0 x0 f x f x f − +  =  =  然后利用 ( ) x0 f −  和 ( ) x0 f +  的 符号证得 ( ) 0. f  x0 = 设函数f ( x)在点x0的某邻域U( x0 )内 且 ( )存在, x0 f  分析 分析 由于 则 f ( x) 在 x = x0 的左导数 ( ) x0 f −  和右导数 ( ) x0 f +  存在 且相等,即 ( )存在, x0 f 

证 对于xo +△x e U(xo),有f(xo + x)≤ f(xo)= f(x +△x)- f(x)≤ 0若 Ax >0, f(x +Ar)-f(xo)≤0;Ax若 Ax<0, f(x +Ar)-f(x)≥ 0;Ax

证 对于 ( ), x0 + x U x0 有 ( ) ( ) 0 x0 f x + x  f  0 若 x  0, x f x x f x  ( +  ) − ( ) 0 0 若 x  0,  0;  0; ( ) ( ) 0 x0  f x + x − f x f x x f x  ( +  ) − ( ) 0 0

费马引理设函数f(x)在点x的某邻域U(x)内有定义，且f(x)存在,如果对VxE U(x),有f(x)≤ f(x)(或f(x)≥ f(x),f'(x.)= f'(x)= fi(x)那么f(x)= 0.由极限的保号性f(xo +△r)- f(xo若 △x >0, '(x)= lim≤0Ar→0+Axf(xo +Ax)- f(xo)若 △x< 0, f'(xo)= lim20ArAr-→0f= 0.UXo函数的！驻点(Stationary point),稳定点临界点(Criticalpoint)

费马引理 有定义, 如果对 ( ), x U x0 有 ( ) ( ) x0 f x  f ( ( ) ( )), x0 或f x  f ( ) 0. 那么 f  x0 = → +  0 lim x f+ (x0 ) = ( ) ( ) ( ) 0 0 x0 f x f x f − +  =  =  f (x0 ) = 由极限的保号性 若 x  0, x f x x f x  ( +  ) − ( ) 0 0  0, 若 x  0,  0. x f x x f x  ( +  ) − ( )  = 0 0 − ( ) x0 f → −  0 lim x  函数的 驻点(Stationary point),稳定点, 临界点(Critical point). 0. 设函数f (x)在点x0的某邻域U(x0 )内 ( ) , 且f  x0 存在

罗尔定理若函数f(x)满足：在闭区间a,bl上连续(1)(2)在开区间a,b)内可导f(a) = f(b);(3)则在开区间(a,b)内至少存在一点使得f'()= 0.分析利用闭区间连续函数的性质和费马引理得出定理结论

罗尔定理 若函数f (x)满足: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) f (a) = f (b); 则在开区间(a,b)内至少存在一点, 使得 f ( ) = 0. 分析 利用闭区间连续函数的性质和费马引理得出 定理结论

罗尔定理若函数f(x)满足：(1)(2) 在开区间a,b)内可导在闭区间a,bl上连续(3)f(a)= f(b),则在开区间(a,b)内至少存在一点使得f()= 0.费马引理设函数f(x)在点x的某邻域U(x)内有定义，且f(x)存在,如果对VxU(x),有f(x)≤ f(x,) (或f(x)≥ f(xo))那么 f'(x)= 0.设 M ± f(a),则在(a,b)内至少存在一点,使f(5)= M. V ≤e[a,b], 有f(x)≤f()由费马引理，f'()=0

(b) 若 M  m. 设 M  f (a),则在(a,b)内至少存在一点 , f ( ) = M. 证 (a) 若 M = m. f (x)在[a,b]有最大值M和最小值m. 则 f (x) = M.得 f (x) = 0.  (a,b),都有 f ( ) = 罗尔定理 若函数f (x)满足: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) f (a) = f (b),则在开区间(a,b)内至少存在一点, 使得 f ( ) = 0. 0. 所以最值不可能同时在端点取得. 使   [a,b], 有 f (x)  f ( ), 由费马引理, f ( ) = 0. 费马引理 有定义, 如果对 ( ), x U x0 有 ( ) ( ) x0 f x  f ( ( ) ( )), x0 或f x  f ( ) 0. 那么 f  x0 = 设函数f (x)在点x0的某邻域U(x0 )内 ( ) , 且f  x0 存在

罗尔定理若函数f(x)满足：(1)在闭区间a,bl上连续(2)在开区间a,b)内可导(3)f(a)= f(b),则在开区间(a,b)内至少存在一点使得f()= 0.注(1)定理条件不全具备,结论不一定成立V4xO1X00x-1x, 0≤x<1f(x) =x , x e[-1,1]f(x) =x,x e[0,1f(x)=0. x=1P

(1) 定理条件不全具备,    =   = 0, 1 , 0 1 ( ) x x x f x f (x) =| x |, x [−1,1] 注 结论不一定成立. 罗尔定理 若函数f (x)满足: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) f (a) = f (b),则在开区间(a,b)内至少存在一点, 使得 f ( ) = 0. 1 x y O − 1 y O x y O x f (x) = x , x [0,1] 1 1

罗尔定理若函数f(x)满足：(1)在闭区间a,bl上连续(2)在开区间a,b)内可导(3)f(a) = f(b),则在开区间(a,b)内至少存在一点使得f()= 0.(2)定理条件只是充分的.本定理可推广为：注设y=f(x)在(a,b)内可导,且lim f(x)= lim, f(x)xa+0h则在(a,b)内至少存在一点,使f()=0.提示f(a+0),x=a证 F(x)在[a,b]上设F(x)=3a<x<b f(x),满足罗尔定理。f(b-0),x=b

(2) 定理条件只是充分的. 本定理可推广为: 在( a , b )内可导,且 = → + lim ( ) 0 f x x a lim ( ) 0 f x x→b− 则在( a , b )内至少存在一点 使 提示      设F(x) = f (a + 0), x = a f (x), a  x  b f (b − 0), x = b 证 F(x)在[a,b]上 满足罗尔定理. 设 罗尔定理 若函数f (x)满足: (1) 在闭区间[a,b]上连续; (2) 在开区间(a,b)内可导; (3) f (a) = f (b),则在开区间(a,b)内至少存在一点, 使得 f ( ) = 0. 注 y = f ( x)