《高等数学》课程教学资源（PPT课件）第四章 不定积分 4-1 第四章 不定积分

#农平4?理学院.2002ULTURAI第四章不定积分

第四章 不定积分

第一节不定积分的概念与性质原函数与不定积分的概念不定积分的性质基本积分公式■小结思考题

第一节 不定积分的概念与性质 ◼ 原函数与不定积分的概念 ◼ 不定积分的性质 ◼ 基本积分公式 ◼ 小结 思考题

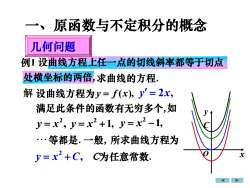
原函数与不定积分的概念一、几何问题例1设曲线方程上任一点的切线斜率都等于切点处横坐标的两倍求曲线的方程解设曲线方程为y=f(x)，y=2x,满足此条件的函数有无穷多个，如y=x2, y=x2+1, y=x2-1,·等都是一般，所求曲线方程为x=x2+C，C为任意常数

一、原函数与不定积分的概念 几何问题 解 例1 设曲线方程上任一点的切线斜率都等于切点 处横坐标的两倍,求曲线的方程. 设曲线方程为 y = f (x), y = 2x, 满足此条件的函数有无穷多个,如 , 2 y = x 1, 2 y = x + 1, 2 y = x −  等都是. 一般, 所求曲线方程为 , 2 y = x + C C为任意常数. x y O C

1.原函数定义1或如果在区间I上，F'(x)= f(x)dF(x) = f(x)dx, 则称 F(x)为f(x)在I上的一个原函数如 (sin x)'=cosx 或由dsin x = cos xdx 知F(x)= sin x是f(x)= cos x在(-o0,+oo)上的一个(F(x)c= sinx+C也是 f(x)= cos x原函数的原函数,其中C为任意常数

定义1 如 (sin x) 1. 原函数 F( x) = f ( x) dF(x) = f (x)dx , 如果在区间I上, 则称 F(x)为f (x)在I上的 或 原函数. = cos x 一个 或由 dsin x = cos xdx 知 F(x) = sin x 是 f (x) = cos x在(− ,+ )上的一个 原函数. F(x) + C 也是 f (x) = cos x 的原函数,其中 C 为任意常数. C C = sin x +C

一般,若F(x)为f(x)的一个原函数 则F(x)+C亦为f(x)的原函数(C为任意常数)因[F(x)+C}' =F'(x) =f(x)一个函数如果有原函数，就有无穷多个如果F(x)是f(x)在区间I上的一个定理结论原函数，则f(x)在区间I上的任一原函数都可表为 F(x)+C 的形式，其中C为某一常数定理表明：形如F(x)+C的一整族函数是(x)的全部原函数

一般, 若F(x) F( x) 亦为f (x) 的原函数(C为任意常数). 因 [F(x) + C] = 一个函数如果有原函数,就有无穷多个. 如果F(x)是f (x) 在区间I上的一个 则 f (x) 在区间I上的任一原函数都 F(x) + C 其中C为某一常数. 则 定理 定理表明: F(x) + C 的一整族函数 F(x) = f ( x). 形如 + C 是f(x)的全部原函数. 为f (x)的一个原函数, 原函数, 结 论 可表为 的形式

定理如果F(αx)是f(x)在区间I上的一个原函数则(x)在区间I上的任一原函数都可表为F(x)+C 的形式,其中C为某一常数证 设G(x)为f(x)的另一个原函数,则G'(x) = f(x),要证F(x)-G(x)=常数又F'()= f(x),因为[G(x)- F(x)J = G'(x)-F'(x)= f(x)- f(x)= 0某个常数导数恒为零的函数必为常数故 F(x)-G(x) =C=>G(x) = F(x)+C只要找到f(x)的一个原函数，就知道它的全部原函数

故 0 F(x) − G(x) = C   =  G(x) − F(x) 0 G(x) = F(x) + C G( x) = f ( x), = f (x) − f (x)  证 设G(x)为f (x) 的另一个原函数,则 又 F( x) = f ( x),G(x) 只要找到f (x)的一个原函数,就知道 它的全部原函数. − F( x)  0 如果F(x)是f (x) 在区间I上的一个原函数, 则f(x)在区间I上的任一原函数都可表为 F(x) + C 其中C为某一常数. 定理 的形式, 要证 F(x) − G(x)  常数 因为 导数恒为零的函数必为常数 某个常数

总和(summa)2.不定积分(1) 定义定义2设F(x)是f(x)的任一原函数则f(x)的全部原函数的一般表达式 F(x)+C[.f(x)dx称为函数f(x)的不定积分.记为Q= F(x)+l积分常数被积表达式积分变量被积函数积分号

积 分 变 量 积 分 常 数 被 积 函 数 定义2 被 积 表 达 式 2. 不定积分 不定积分. (1) 定义 则f (x)的全部原函数的一般表达式 F(x) + C 称为函数f (x)的 总和(summa) f (x)dx 记为  积 分 号 f x x = F x + C  ( )d ( ) 设F(x)是f (x)的任一原函数

[f(x)dr=d[F(x)+C]1.被积函数是原函数的导数，被积表达式是原函数的微分2.不定积分表示那些导数等于被积函数的所有函数．或说其微分等于被积表达式的所有函数.因此绝不能漏写积分常数C3.求已知函数的原函数或不定积分的运算称为积分运算，它是微分运算的逆运算

=dF( x) + C   1. 被积函数是原函数的导数, 被积表达式是 原函数的微分.  f (x)dx 2. 不定积分表示那些导数等于被积函数的所 或说其微分等于被积表达式的所 有函数. 有函数. 因此绝不能漏写积分常数C. 3. 求已知函数的原函数或不定积分的运算称 为积分运算, 它是微分运算的逆运算

例2 求[x'dx.F(x)J解+C=x6dx.例3求1+xF(x)1解arctan x21+ xdx = arctan x +C

例2 求 d . 5 x x  解  =  x dx 5 解 例3 求 2 1 d . 1 x + x  ( ) =  F( x) C x + 6 6 2 1 1 + x  = +  x x d 1 1 2 arctan x arctan x +C ( ) 5 = x  6 6 x F( x)

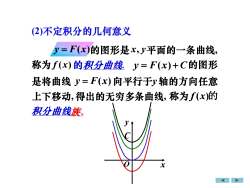
(2)不定积分的几何意义y=F(x)的图形是x,y平面的一条曲线称为f(x）的积分曲线y=F(x)+C的图形是将曲线 =F(x)向平行于y轴的方向任意上下移动,得出的无穷多条曲线，称为,f(x)的积分曲线族X

(2)不定积分的几何意义 积分曲线 y = F(x) 称为 f ( x) 的积分曲线. y = F(x) + C 的图形 y = F(x) 向平行于y 轴的方向任意 上下移动, 得出的无穷多条曲线, 称为 f (x)的 的图形是 x, y 平面的一条曲线, 是将曲线 族. x y O C