《高等数学》课程教学资源（PPT课件）第六章 定积分的应用 6-3 第三节 定积分在物理学上的应用

第三节定积分在物理学上的应用变力沿直线所作的功一、二、 水压力三、 引力四、小结思考题

一、 变力沿直线所作的功 二、 水压力 三、 引力 四、 小结 思考题 第三节 定积分在物理学上的应用 1

一、变力沿直线所作的功由物理学知道，如果物体在作直线运动的过程中有一个不变的力F作用在这物体上，且这力的方向与物体的运动方向一致，那么，在物体移动了距离s时，力F对物体所作的功为W=F.s.如果物体在运动的过程中所受的力是变化的，就不能直接使用此公式，而采用“微元法思想

由物理学知道，如果物体在作直线运动的 过程中有一个不变的力F 作用在这物体上，且 这力的方向与物体的运动方向一致，那么，在 物体移动了距离s时，力F 对物体所作的功为 W = F s. 如果物体在运动的过程中所受的力是变化 的，就不能直接使用此公式，而采用“微元法” 思想. 一、变力沿直线所作的功 2

例1把一个带+α电量的点电荷放在 r轴上坐标原点处，它产生一个电场：这个电场对周围的电荷有作用力．由物理学知道，如果一个单位正电荷放在这个电场中距离原点为r的地方，那么电场对它的作用力的大小为 F=k（k是常数），当这个单位正电荷在电场中从r=a处沿r轴移动到r=b 处时，计算电场力F 对它所作的功3

例 1 把一个带 + q 电量的点电荷放在 r 轴上坐 标原点处，它产生一个电场．这个电场对周围的电 荷有作用力．由物理学知道，如果一个单位正电荷 放在这个电场中距离原点为 r 的地方，那么电场 对它的作用力的大小为 2 r q F = k （k是常数），当 这个单位正电荷在电场中从 r = a 处沿 r 轴移 动到 r = b 处时，计算电场力 F 对它所作的功． 3

+1+q解取r为积分变量，ar+dr b0r e[a,b],kqdr.取任一小区间[r,r+drl，功元素dw所求功为W=kgb2如果要考虑将单位电荷移到无穷远处KOa

解 取r 为积分变量， o r • + q a  b • •• • • • • + 1 r r [a,b],  r + dr 取任一小区间[r,r + dr], 功元素 , 2 dr r kq dw = 所求功为 dr r kq w b a = 2 b a r kq       = − 1 . 1 1       = − a b kq 如果要考虑将单位电荷移到无穷远处 dr r kq w a + = 2 +       = − a r kq 1 . a kq = 4

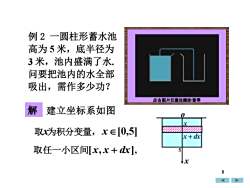
例2 一圆柱形蓄水池高为5米，底半径为3米，池内盛满了水.问要把池内的水全部吸出，需作多少功？点击图片任意处播放暂停解建立坐标系如图取x为积分变量，xE[0,5]x+ dx取任一小区间[x,x+dxl5X5

点击图片任意处播放\暂停 例 2 一圆柱形蓄水池 高为 5 米，底半径为 3 米，池内盛满了水. 问要把池内的水全部 吸出，需作多少功？ 解 建立坐标系如图 x o x 取 x + dx x为积分变量， x[0,5] 取任一小区间[x, x + dx], 5 5

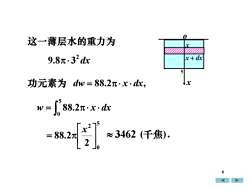
0这一薄层水的重力为x + dx9.8元.3°dx5功元素为dw=88.2元?x?dx+x488.2元·x·dxW=0273X～3462 (千焦).=88.2元2

x o x x + dx 5 这一薄层水的重力为 dx 2 9.8 3 功元素为 dw = 88.2 x  dx, w =  x  dx  88.2 5 0 5 0 2 2 88.2       =  x  3462 (千焦)． 6

例3用铁锤把钉子钉入木板，设木板对铁钉的阻力与铁钉进入木板的深度成正比，铁锤在第一次锤击时将铁钉击入1厘米，若每次锤击所作的功相等，问第次锤击时又将铁钉击入多少？解设木板对铁钉的阻力为 f(x)= kx,k第一次锤击时所作的功为 w, =「f(x)dx=2设n次击入的总深度为h厘米Wn = (" f(x)dxn次锤击所作的总功为

解 设木板对铁钉的阻力为 f (x) = kx, 第一次锤击时所作的功为  = 1 0 1 w f (x)dx , 2 k = ( ) . 0 = h wh f x dx 例3 用铁锤把钉子钉入木板，设木板对铁钉的阻 力与铁钉进入木板的深度成正比，铁锤在第一次 锤击时将铁钉击入1厘米，若每次锤击所作的功 相等，问第 次锤击时又将铁钉击入多少？ n 设 n 次击入的总深度为 h 厘米 n 次锤击所作的总功为 7

kh?kxdxWh=2依题意知，每次锤击所作的功相等kh?kWh = nWi =)2'2n次击入的总深度为h=/n,第n次击入的深度为 /n一/n-1.S

 = h h w kxdx 0 , 2 2 kh = 依题意知，每次锤击所作的功相等． wh = nw1  2 2 kh , 2 k = n h = n, n − n − 1. n 次击入的总深度为 第 n 次击入的深度为 8

二、水压力由物理学知道,在水深为h处的压强为p=Pgh这里β是水的密度,g是重力加速度．如果有一面积为A的平板水平地放置在水深为h处那么.平板一侧所受的水压力为P=p·A.如果平板垂直放置在水中，由于水深不同的点处压强p不相等，平板一侧所受的水压力就不能直接使用此公式，而采用“微元法”思想

由物理学知道,在水深为h处的压强为 p gh =  , 这 里  是水的密 度, g 是重力加速 度．如果有一面积 为A的平板水平地放置在水深为h处,那 么,平板一侧 所受的水压力为 P = p A． 如果平板垂直放置在水中，由于水深不同 的点处压强p不相等，平板一侧所受的水压力 就不能直接使用此公式，而采用“微元法” 思 想． 二、水压力 9

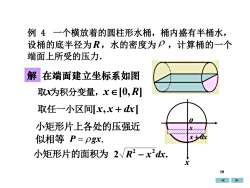
例 4一个横放着的圆柱形水桶，桶内盛有半桶水设桶的底半径为R，水的密度为P，计算桶的一个端面上所受的压力解在端面建立坐标系如图取x为积分变量，xE0,R取任一小区间[x,x+dx]小矩形片上各处的压强近x似相等 P=pgx,小矩形片的面积为 2√R2一x2dxx10

例 4 一个横放着的圆柱形水桶，桶内盛有半桶水， 设桶的底半径为R，水的密度为  ，计算桶的一个 端面上所受的压力． 解 在端面建立坐标系如图 x o 取x为积分变量，x[0,R] 取任一小区间[x, x + dx] x x + dx 小矩形片上各处的压强近 似相等 小矩形片的面积为 2 . 2 2 R − x dx P gx =  , 10