《高等数学》课程授课教案（讲义）第五章 定积分

第五章定积分$5.1定积分的概念教学目的：理解定积分的定义教学重点：连续变量的累积教学难点：连续变量的累积教学内容：一、定积分举例：1、曲边梯形面积设y=f(x)在[a,b]上非负，连续，由直线x=a,x=b,y=0及曲线y=f(x)所围成的图形，称为曲边梯形。求面积：在区间[a,b]中任意插入若干个分点a=xo<x<x2<xn-1<x，=b，把[a,b]分成n个小区间[o,x],[x,X2], .-[xn-1,x,],它们的长度依次为：Ax,=Xi-Xo,Ax, =X2-xi,",Ax,=X,-Xn-1经过每一个分点作平行于y轴的直线段，把曲边梯形分成n个窄曲边梯形在每个小区间[xi-1,x,]上任取一点5，以[xi-,x,]为底，F(5)为高的窄边矩形近似替代第i个窄边梯形（i=1,2,n），把这样得到的n个窄矩形面积之和作为所求曲边梯形面积A的近似值，即A= f(5,)Ax, + f(5)Ar, +..+ f(5,)Ax-2 f(5,)Ax,设=max(Ax,Ax2…Ax→0时，可得曲边梯形的面积A = lim f(5)Ax,A-01=1140

140 第五章 定积分 §5.1 定积分的概念 教学目的：理解定积分的定义 教学重点：连续变量的累积 教学难点：连续变量的累积 教学内容： 一、定积分举例： 1、 曲边梯形面积 设 y = f (x)在 [ ] a,b 上非负，连续，由直线 x = a, x = b, y = 0 及曲线 y = f (x) 所围成的图形，称为曲边梯形。 求面积： 在区间 [a,b] 中任意插入若干个分点 a = x0 < x1 < x2 " < xn−1 < xn = b ，把[a,b]分成 n 个小区间 [ 0 1 x , x ],[ 1 2 x , x ], . [ n n x , x −1 ], 它们的长度依次为： 1 1 0 2 2 1 1 , , , Δ = − Δ = − Δ n = n − n− x x x x x x " x x x 经过每一个分点作平行于 y 轴的直线段，把曲边梯形分成 n 个窄曲边梯形， 在每个小区间[ i i x , x −1 ]上任取一点ξ i ，以[ i i x , x −1 ]为底， ( )i f ξ 为高的窄边矩形近 似替代第i 个窄边梯形（i=1,2,.,n）,把这样得到的 n 个窄矩形面积之和作为所求 曲边梯形面积 A 的近似值，即 i n n A ≈ f ( )Δx + f ( )Δx + + f ( )Δx ξ 1 ξ 2 2 " ξ =∑= Δ n i i i f x 1 (ξ ) 设λ = max{Δx1 ,Δx2 ,"Δxn },λ → 0时，可得曲边梯形的面积 ∑= → = Δ n i i i A A f x 1 0 lim (ξ )

2、变速直线运动的路程设某物体作直线运动，已知速度v=v(t)是时间间隔[T,T,]上t的连续函数，且vt≥O)，计算在这段时间内物体所经过的路积S在[T,T,]内任意插入若干个分点T =to 0i=l141

141 2、 变速直线运动的路程 设某物体作直线运动，已知速度v = v(t) 是时间间隔[ 1 2 T ,T ]上 t 的连续函数， 且v(t ≥ 0) ，计算在这段时间内物体所经过的路积 S 在[ 1 2 T ,T ]内任意插入若干个分点 1 0 1 2 1 T2 T t t t t t = < < < " n− < n = 把[ 1 2 T ,T ]分成 n 个小段 [ 0 1 t ,t ]，[ 1 2 t ,t ]，.， [ n n t ,t −1 ] 各小段时间长依次为： , , , , Δ 1 = 1 − 0 Δ 2 = 2 − 1 Δ n = n − n−1 t t t t t t " t t t 相应各段的路程为： ΔS ΔS ΔSn , , , 1 2 " 在[ i i t ,t −1 ]上任取一个时刻 ( ) i i 1 i i T t ≤ T ≤ t − ，以Ti 时的速度 ( ) Ti v 来代替[ i i t ,t −1 ] 上各个时刻的速度，则得： i i i Δ S ≈ v (T ) Δ t ) (i = 1,2,",n 进一步得到： n n S ≈ v(T )Δt + v(T )Δt + + v(T )Δt 1 1 2 2 " =∑= Δ n i v T t 1 1 1 ( ) 设λ = max{ } Δt1 ,Δt2 ,",Δtn ,当λ → 0 时， 得： ∑= → = Δ n i i S v T t 1 0 lim ( ) λ 二、定积分的定义 由上述两例可见，虽然所计算的量不同，但它们都决定于一人函数及其自变 量的变化区间，其次它们的计算方法与步骤都相同，即归纳为一种和式极限，即 面积 ∑= → = Δ n i i i A f x 1 0 lim (ξ ) λ

路程S=limZv(T,)At,1→0将这种方法加以精确叙述得到定积化的定义定义设函数f(x)在[a,b]上有界，在[a,b]中任意插入若干个分点a=X<x <x2 <...<xn- <x,=b把区间[a,b]分成n个小区间[xo,x],[x,x2],,[xn-1,x,],各个小区间的长度依次为Ax=x-xo,Ax2=x2-x,,Ax,=x,-Xn-1在每个小区间[x-1,x,]上任取一点s(x-≤6,≤x,),作函数值f(c)与小区间长度Ax,的乘积f(s,)Ax,(i=1,2,.,n),并作出和S=2f(6,)Ax,记=max(Axi,Ar2,,Ar},如果不论对[a,b]怎样分法,也不论在小区间[xi-1,x,]上点s怎样取法，只要当入→1时，和S总趋于确定的极限1,这时我们称这个极限1为函数f(x)在区间[a,b)上的定积分(简称积分),记作["f(x)dx,即I(x)dx=I=lim之(s,)Ax,20其中f(x)叫做被积函数，f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b叫做积分上限，[a,b]叫做积分区间注意：积分与积分变量无关，即："(x)dx=I"()dt =I'(u)du函数可积的两个充分条件：定理1设f(x)在[a,b]上连续，则f(x)在[a,b]上可积。定理2设f(x)在[a,b]上有累，且只有有限个间断点，则f(x)在[a,b]上可积。例：利用定积分定义计算【x2dx142

142 路程 ∑= → = Δ n i i i S v T t 1 0 lim ( ) λ . 将这种方法加以精确叙述得到定积化的定义 定义 设函数 f (x)在[a,b]上有界，在[a,b]中任意插入若干个分点 a = x0 < x1 < x2 < " < xn−1 < xn = b 把区间[a,b]分成n 个小区间 ], [ , ],[ , ], ,[ , 0 1 1 2 n 1 n x x x x x x " − 各个小区间的长度依次为 1 1 0 2 2 1 1 , , , Δ = − Δ = − Δ n = n − n− x x x x x x " x x x . 在每个小区间[ i i x , x −1 ]上任取一点 i i i i x ≤ ≤ x − ε ε 1 ( ),作函数值 ( )i f ε 与小区间长度 i Δx 的乘积 f ( ) x (i 1,2, ,n), ε i Δ i = " 并作出和 ∑= = Δ n i i i S f x 1 (ε ) . 记 max{ , , , } 1 2 n λ = Δx Δx " Δx ,如果不论对[a,b]怎样分法,也不论在小区间[ i i x , x −1 ] 上点 i ε 怎样取法,只要当λ →1时,和 S 总趋于确定的极限 I ,这时我们称这个极限 I 为函数 f (x) 在区间[a,b]上的定积分(简称积分),记作 ∫ b a f (x)dx ,即 ∫ b a f (x)dx = I = ∑= → Δ n i i i f x 1 0 lim (ε ) λ , 其中 f (x) 叫做被积函数, f (x)dx 叫做被积表达式, x 叫做积分变量, a 叫做积分下 限,b 叫做积分上限, [a,b]叫做积分区间. 注意：积分与积分变量无关，即： ∫ ∫∫ = = b a b a b a f (x)dx f (t)dt f (u)du 函数可积的两个充分条件： 定理 1 设 f (x)在[a,b]上连续，则 f (x) 在[a,b]上可积。 定理 2 设 f (x)在[a,b]上有累，且只有有限个间断点，则 f (x)在[a,b]上可积。 例：利用定积分定义计算 ∫ 1 0 2 x dx

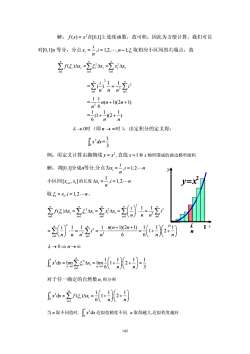
解：f(x)=x在[0,1]上连续函数，故可积，因此为方便计算，我们可以1对[0,1]n等分，分点x,=,i=1,2n-15取相应小区间的右端点，故n2 f(5)Ar, =2A,-2x,Ax,台i=li=lZ(一)Ti-3/nn=lnis11n(n + 1)(2n + 1)n36(+)(2+)6nn入一0时（即n一80时），由定积分的定义得：x'dx=!3例：用定义计算由抛物线y=x2直线x=1和x轴所围成的曲边梯形面积I解：将[0,1]分成n等分,分点为x,=,i=1,2...nVn,i=1,2..n小区间[x-,x,]的长度Ax,=V:n取5,=x,i=1,2..-n,2F(5)Ax, =254 =2xAx =13nn=(n)1i=l-112() -111/2+11+-=1660210=→T rdx=lm≥54x,=lim(1+=2+=-1-→04n→6nni=l对于任一确定的自然数n.积分和r'dx ~Zf(5)Ax =-2+1+当n取不同值时，x2dx近似值精度不同.n取得越大,近似程度越好，143

143 解： 上 ( ) 在[0,1] 2 f x = x 连续函数，故可积，因此为方便计算，我们可以 对[0,1]n 等分，分点 i n i i n i x = , = 1,2,", −1;ξ 取相应小区间的右端点，故 ∑ ∑ ∑ = = = Δ = Δ = Δ n i i i n i i i n i i i f x x x x 1 2 1 2 1 (ξ ) ξ =∑ ∑ = = = n i n i i n n n i 1 2 3 2 1 1 1 ( ) = ( 1)(2 1) 6 1 1 3 n n + n + n = ) 1 )(2 1 (1 6 1 n n + + λ → 0时（即n → ∞时），由定积分的定义得： ∫ 1 0 2 x dx = 3 1 例：用定义计算由抛物线 2 y = x , 直线 x =1和 x 轴所围成的曲边梯形面积. 解： [0,1] , , 1,2 i i n xi n n 将 分成 等分 分点为 = = " 小区间 1 [ ,] i i x x − 的长度 1 , 1,2 i x i n n Δ= = " 取 , 1,2 i i ξ = = x i n " ， 2 2 1 11 ( ) n nn i i i i ii i ii f ξ ξ x x xx = == ∑ ∑∑ Δ= Δ= Δ 2 2 3 1 1 1 1 n n i i i i = = n nn ⎛ ⎞ = ⋅= ⎜ ⎟ ⎝ ⎠ ∑ ∑ 2 2 3 3 1 1 1 1 1 ( 1)(2 1) 1 1 1 1 2 6 6 n n i i i nn n i = = n nn n n n ⎛ ⎞ ⎛ ⎞⎛ ⎞ + + = ⋅= = ⋅ = + + ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠⎝ ⎠ ∑ ∑ λ → ⇒ →∞ 0 n 1 2 2 0 0 1 1 1 11 d lim lim 1 2 6 3 n i i n i xx x λ n n ξ → →∞ = ⎛ ⎞⎛ ⎞ = Δ= + + = ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ ∫ ∑ 对于任一确定的自然数n, 积分和 1 2 0 1 11 1 d () 1 2 6 n i i i xx f x n n ξ = ⎛ ⎞⎛ ⎞ ≈ Δ= + + ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ ∫ ∑ 当 n 取不同值时, 1 2 0 x dx ∫ 近似值精度不同. n 取得越大,近似程度越好. n i 2 y=x 1 y O x

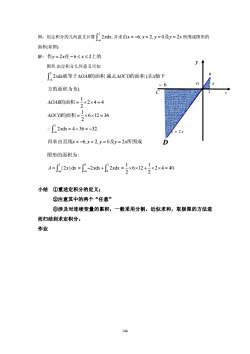
例：用定积分的几何意义计算2xdx,并求由x=-6,x=2,y=0及y=2x所围成图形的面积(如图）解：作y=2x在-6≤x≤2上的y图形，由定积分几何意义可知B2xdx就等于△OAB的面积减去△OCD的面积（在x轴下0A6一方的面积为负）C2AOAB的面积=×2×4=42△OCD的面积=-x6x12=3622xdx=4-36=-32D再求由直线x=-6,x=2,y=0及y=2x所围成图形的面积为：A=[",12x| dx =J~-2xdx+f,2xdx = -×6×12+=×2×4=4022小结①重述定积分的定义；②注意其中的两个“任意”③涉及对连续变量的累积，一般采用分割，近似求和，取极限的方法进而归结到求定积分。作业144

144 例：用定积分的几何意义计算 2 6 2d, x x ∫− 并求由 及 x = −= = = 6, 2, 0 2 x y yx 所围成图形的 面积(如图). 解：作 在 上的 yx x = −≤≤ 26 2 图形,由定积分几何意义可知 2 6 2 dx x OAB − Δ ∫ 就等于 的面积 减去 的面积 在 轴下 ΔOCD x ( 方的面积为负). 1 24 4 2 Δ = ×× = OAB的面积 1 6 12 36 2 Δ = ×× = OCD的面积 2 6 2 d 4 36 32. x x − ∴ = − =− ∫ 再求由直线 及 所围成 x x y yx = −= = = 6, 2, 0 2 图形的面积为: 2 6 A xx |2 |d − = ∫ 0 2 6 0 2d 2d x x xx − =− + ∫ ∫ 1 1 6 12 2 4 40. 2 2 = ×× + ×× = 小结 ①重述定积分的定义； ②注意其中的两个“任意” ③涉及对连续变量的累积，一般采用分割，近似求和，取极限的方法进 而归结到求定积分。 作业 y = 2 x A 2 − 6 x y O D B C

$5.2定积分的性质教学目的：掌握定积分的性质，特别是中值定理教学重点：熟练运用性质教学难点：中值定理教学内容：定积分的性质为方便定积分计算及应用，作如下补充规定：(1）当 a=b时，「'f(x)dx=0(2)当a>b时，["(x)dx=-"f(x)dx性质1函数和（差）的定积分等于它们的定积分的和（差），即'(x)±g(x)x=I(x)dx± J'g(x)dx证明: ["L(t)±g()dx= lim之(5)±g(5)Ax;-()4+(0),11.04" f(x)dx± [ g(x)dx性质2被积函数的常数因子可以提到积分号外面，即["kf(x)dx=k ["f(x)dx(k 是常数)性质3如果将积分区间分成两部分，则在整个区间上的定积分等于这两个区间上定积分之和，即设a<c<b,则'f(x)dx= I" (x)dx+ " f(x)dx注意：我们规定无论a,b,c的相对位置如何，总有上述等式成立。性质4如果在区间[a,b) 上，f(x)=1,则[ f(x)dx=["dx=b-c性质5如果在区间[a,b]上，f(x)≥0,则["f(x)dx≥0 (a<b)证明：因f(x)≥0,故f(5)≥0(i=1,2,3,",n)，又因145

145 §5.2 定积分的性质 教学目的：掌握定积分的性质，特别是中值定理 教学重点：熟练运用性质 教学难点：中值定理 教学内容：定积分的性质 为方便定积分计算及应用，作如下补充规定： （1） 当 a=b 时， ( ) = 0 ∫ b a f x dx （2） 当 a>b 时， = − ∫ b a f (x)dx ∫ a b f (x)dx 性质 1 函数和（差）的定积分等于它们的定积分的和（差），即 ± = ∫ f x g x dx b a [ ( ) ( )] ± ∫ b a f (x)dx ∫ b a g(x)dx 证明： ± = ∫ f x g x dx b a [ ( ) ( )] i n i i i ∑ f ± g Δx = → 1 0 lim [ (ξ ) (ξ )] λ = ∑ Δ ± = → i n i i f x 1 0 lim (ξ ) λ i n i i ∑g Δx = → 1 0 lim (ξ ) λ = ± ∫ b a f (x)dx ∫ b a g(x)dx 性质 2 被积函数的常数因子可以提到积分号外面，即 = ∫ b a kf (x)dx k ∫ b a f (x)dx ( k 是常数) 性质 3 如果将积分区间分成两部分，则在整个区间上的定积分等于这两 个区间上定积分之和，即设 a<c<b,则 = ∫ b a f (x)dx ∫ + c a f (x)dx ∫ b c f (x)dx 注意：我们规定无论 a,b,c 的相对位置如何，总有上述等式成立。 性质 4 如果在区间[a,b] 上， f (x) ≡ 1,则 = ∫ b a f (x)dx dx b a b a = − ∫ 性质 5 如果在区间[a,b] 上， f (x) ≥ 0,则 ( ) ≥ 0 ∫ b a f x dx (a < b) 证明：因 f (x) ≥ 0,故 f ( ) 0(i 1,2,3, ,n) ξ i ≥ = " ，又因

Ax, ≥0(i= 1,2,,n),故f(5,)Ax, ≥0,i=l设=maxAr,Ax,Ar,,→o时，便得欲证的不等式。推论1如果在[a,b] 上，f(x)≤g(x),则["f(x)dx≤J'g(x)dx (ab，还是a0.. [°(e*-x)dx>0: L,e'dx>L,xdx 于是,e'dx34146

146 x 0(i 1,2, ,n) Δ i ≥ = " ，故 ( ) 0 1 ∑ Δ ≥ = i n i i f ξ x ， 设λ = max{Δx1 ,Δx2 ,",Δxn },λ → o时，便得欲证的不等式。 推论 1 如果在[a,b] 上， f (x) ≤ g(x),则 ≤ ∫ b a f (x)dx ∫ b a g(x)dx （ab，还是 a∴ − > ∵ ∫ 0 0 2 2 d d x e x xx − − ∴ > ∫ ∫ 于是 2 2 0 0 d d x e x xx − − < ∫ ∫ 例：估计积分 3 0 1 d . 3 sin x x π + ∫ 的值 解： 3 1 ( ) 3 sin f x x = + ，∀ ∈x [0, ] π 3 0 sin 1 ≤ ≤x 3 111 4 3 sin 3 x ≤ ≤ + 3 00 0 111 d dd 4 3 sin 3 x x x x ππ π ≤ ≤ + ∫ ∫ ∫ 、 3 0 1 d 4 3 sin 3 x x π π π ≤ ≤ + ∫

sin×dx的值例：估计积分xsinx解：f(x)=xxcosx-sinx_cosx(x-tanx)<0f'(x)=x2x2元元元元f(x)eCf(x）在4°242/22,m=f(3)=M=f(").b-a=244元A2V22.元212元sin.x2dr元2A2元4xrna sin Xdx = 0例：求证lim(a为常数)X证：由积分中值定理有sin5n(n+a-n)In+a sinx.dx(n≤E,≤n+aJn5nxsin 5n a = 0n+asinxlimdx = lim5n+n-→o[sinnxsin"xdx= 0例：求证lim证：当xe0,时, sin xsin"x(sin) -4.41”元→ 0(n → )[ sin nx sin" xdx≤0≤)47夹逼定理即得limsinnxsin"xdx=0小结：本小结讲述了定积分的性质、积分中值定理作业：147

147 例：估计积分 2 4 sin d . x x x π ∫π 的值 解： sin ( ) x f x x = 2 2 cos sin cos ( tan ) () 0 x x x xx x f x x x − − ′ == < () , , 4 2 fx C ⎡ ⎤ π π ∈ ⎢ ⎥ ⎣ ⎦ () , 4 2 f x ⎡ ⎤ π π ⎢ ⎥ ⎣ ⎦ 在 上 2 2 () , 4 M f π π = = 2 () , 2 m f π π = = 4 b a π − = 2 4 1 2 sin 2 2 2 2 4 42 x dx x π π π π π π =⋅≤ ≤ ⋅= ∫ 例： sin lim d 0 n a n n x x x + →∞ = 求证 ∫ (a 为常数) 证：由积分中值定理有 sin sin d () n a n n n x x nan x ξ ξ + = +− ∫ (n na ≤ ξ n ≤ + ) sin sin lim d lim 0 n a n n n n n x x a x ξ ξ + →∞ →∞ = = ∫ 例： 4 0 lim sin sin d 0 n n nx x x π →∞ = 求证 ∫ 证： 0, , 4 x ⎡ ⎤ π ∈ ⎢ ⎥ ⎣ ⎦ 当 时 1 | sin sin | sin 4 2 n n n nx x ⎛ ⎞ π ⎛ ⎞ ≤ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ 4 0 1 0 sin sin d 0( ) 2 4 n n nx x x n π ⎛ ⎞ π ≤ ≤ ⋅ → →∞ ⎜ ⎟ ⎝ ⎠ ∫ 夹逼定理 即得 4 0 lim sin sin d 0 n n nx x x π →∞ = ∫ 小结：本小结讲述了定积分的性质、积分中值定理 作业:

$5.3微积分基本公式教学目的：掌握微积分基本公式及其应用教学重点：公式的应用教学难点：公式的应用教学内容：一、变速直线运动中位置函数与速度函数之间的联系设一物体在一直线上运动，在这直线上取定原点，正方向，单位长度，使其成为一数轴，时刻t时物体所有的位置s(t)，速度v(t)(不防设v()≥0)。物体在时间间隔[T,T,]内经过的路程可以用速度函数v(t)在[T,T,]上的定积分来表达，即["v(0)dx另一方面，这段路程可以通过位置函数s()在区间[T,T,]的增量来表示，即S(T,)- S(T)故["v(1)dx=S(T,) - S(T,)注意到S (t)=v(t)，即s(t)是v(t)的原函数。二、积分上限的函数及其导数设f(x)在[a,b]上连续，并且设x为[a,b]上任一点，设d(x)= f(t)dt函数Φ(x)具有如下性质：定理1如果函数f(x)在区间[a,b]上连续，则积分上限函数d(x)=f, f(t)dt在[a,b]上具有导数，并且它的导数是dr'fodtΦ(x)=dxJa148

148 §5.3 微积分基本公式 教学目的：掌握微积分基本公式及其应用 教学重点：公式的应用 教学难点：公式的应用 教学内容： 一、变速直线运动中位置函数与速度函数之间的联系 设一物体在一直线上运动，在这直线上取定原点，正方向，单位长度，使其 成为一数轴，时刻 t 时物体所有的位置s(t)，速度v(t)(不防设v(t) ≥ 0)。 物体在时间间隔[ , ] T1 T2 内经过的路程可以用速度函数v(t)在[ , ] T1 T2 上的定积 分来表达，即 ∫ 2 1 ( ) T T v t dx 另一方面，这段路程可以通过位置函数s(t)在区间[ , ] T1 T2 的增量来表示，即 ( ) ( ) 2 T1 S T − S 故 ∫ 2 1 ( ) T T v t dx = ( ) ( ) 2 T1 S T − S 注意到S`(t) = v(t)，即s(t)是v(t)的原函数。 二、积分上限的函数及其导数 设 f (x) 在[a,b]上连续，并且设 x 为[a,b]上任一点，设 ∫ Φ = x a (x) f (t)dt 函数Φ(x) 具有如下性质： 定理 1 如果函数 f (x) 在区间[a,b]上连续，则积分上限函数 ∫ Φ = x a (x) f (t)dt 在[a,b]上具有导数，并且它的导数是 ∫ Φ′ = x a f t dt dx d (x) ( )

(a≤x≤b)=f(x)证明：（1）xe(a,b)时，A(x) = Φ(x + Ax)-Φ(x)-f* f()dt- f()dt** f(t)dt= f(3)Ar在x与Ax之间A() = f(5)AxAx→0时，有Φ(x)= f(x)（2）x=a或b时考虑其单侧导数，可得Φ(a)= f(a), Φ(b)= f(b)由定理1可得下面结论定理2如果函数f(x)在区间[a,b]上连续，则函数'f(t)dtd(x) = 是f(x)的一个原函数。三、Newton一Leibniz公式定理3如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数，则J" f(x)dx = F(b)- F(a)证明：因F(x)与Φ(x)均是f(x)原函数，故F(x)-Φ(x)=c(a≤x≤b)又因 f(x)dx = Φ(b)- Φ(a)故[f(x)dx= F(b)- F(a)为方便起见，把F(b)-F(a)记作[F(x)]149

149 = ) f (x （a ≤ x ≤ b） 证明：（1） x ∈ (a,b) 时， ΔΦ(x) = Φ(x + Δx) − Φ(x) = − ∫ x+ x a f t dt 4 ( ) ∫ x a f(t)dt = f t dt f x x x x = Δ ∫ + ( ) ( ) 4 ξ ξ 在 x与 之间 Δx ( ) ( ) f ξ x x = Δ ΔΦ Δx → 0时，有 Φ′(x) = f (x) （2） x = a或b时考虑其单侧导数，可得 Φ′(a) = f (a) ，Φ′(b) = f (b) 由定理 1 可得下面结论 定理 2 如果函数 f (x) 在区间[a,b]上连续，则函数 Φ(x) = ∫ x a f(t)dt 是 f (x) 的一个原函数。 三、Newton —Leibniz 公式 定理 3 如果函数 F(x)是连续函数 f (x) 在区间[a,b]上的一个原函数，则 = ∫ b a f (x)dx F(b) − F(a) 证明：因 F(x)与Φ(x) 均是 f (x) 原函数，故 F(x) − Φ(x) =c （a ≤ x ≤ b） 又因 = ∫ b a f (x)dx Φ(b) − Φ(a) 故 = ∫ b a f (x)dx F(b) − F(a) 为方便起见，把 F(b) − F(a) 记作[ ) F(x ] b a