《高等数学》课程授课教案（讲义）第九章 重积分

第九章重积分$9.1二重积分的概念与性质教学目的：在深刻理解的基础上熟练掌握二重积分的概念、性质教学重点：二重积分的概念教学难点：二重积分概念的理解教学内容：一、二重积分的概念1、曲顶柱体的体积设有一空间立体Q,它的底是XOy面上的有界区域D,它的侧面是以D的边界曲线为准线,而母线平行于z轴的柱面,它的顶是曲面z=f(x,J)。当(x,Jy)eD时,f(x,J)在D上连续且(x,J)≥0,以后称这种立体为曲顶柱体。曲顶柱体的体积可以这样来计算，(I)、用任意一组曲线网将区域D分成n个小区域△o,2，",A，以这些小区域的边界曲线为准线，作母线平行于z轴的柱面，这些柱面将原来的曲顶柱体2分划成n个小曲项柱体△2，22，,2。A2;,这里0i既代表第1个小区域,又表（假设i所对应的小曲顶柱体为示它的面积值,42"i既代表第i个小曲顶柱体,又代表它的体积值。）

第九章 重积分 §9.1 二重积分的概念与性质 教学目的：在深刻理解的基础上熟练掌握二重积分的概念、性质 教学重点：二重积分的概念 教学难点：二重积分概念的理解 教学内容： 一、二重积分的概念 1、曲顶柱体的体积 设有一空间立体Ω,它的底是 xoy 面上的有界区域 D,它的侧面是以 D的边 界曲线为准线,而母线平行于 z 轴的柱面,它的顶是曲面 z = f (, ) x y 。 当(, ) x y D∈ 时, f (, ) x y 在 D 上连续且 f (, ) x y ≥ 0 ,以后称这种立体 为曲顶柱体。 曲顶柱体的体积V 可以这样来计算: (1)、用任意一组曲线网将区域 D分成n 个小区域 Δσ 1 2 , , Δσ " Δσ n ,以这 些小区域的边界曲线为准线,作母线平行于 z 轴的柱面,这些柱面将原来的曲顶柱 体Ω分划成n 个小曲顶柱体 ΔΩ1 2 , , ΔΩ " ΔΩn 。 （假设 Δσ i 所对应的小曲顶柱体为 ΔΩi ,这里 Δσ i 既代表第 i 个小区域,又表 示它的面积值, ΔΩi 既代表第i 个小曲顶柱体,又代表它的体积值。)

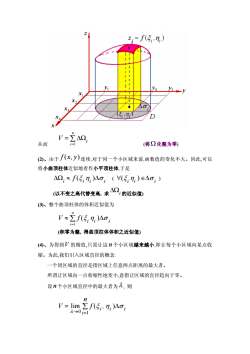
z,=f(5,.n.)JiY4YsXX(5iV=AQ从而i=1（将Q化整为零）(2)、由于F(x,J)连续,对于同一个小区域来说,函数值的变化不大。因此,可以将小曲顶柱体近似地看作小平顶柱体,于是A2, ~f(5,n,)Ao,(V(5,n,)eAo, )(以不变之高代替变高, 求 A2 的近似值)(3)、整个曲顶柱体的体积近似值为V~Z f(5,n,)A0i=(积零为整，得曲顶柱体体积之近似值）(4)、为得到V的精值,只需让这n个小区域越来越小,即让每个小区域向某点收缩。为此，我们引入区域直径的概念个闭区域的直径是指区域上任意两点距离的最大者。所谓让区域向一点收缩性地变小，意指让区域的直径趋向于零。设n个小区域直径中的最大者为，则nV = lim Z f(5,, n,)Ao;->0i=1

从而 V i i n = = ∑ ΔΩ 1 (将Ω化整为零) (2)、由于 f (, ) x y 连续,对于同一个小区域来说,函数值的变化不大。因此,可以 将小曲顶柱体近似地看作小平顶柱体,于是 ΔΩ Δ Δ i ii i ii i ≈ f () () ξ η σ ( ) ∀ ξ η ∈ σ (以不变之高代替变高, 求ΔΩi 的近似值) (3)、整个曲顶柱体的体积近似值为 V f ii i i n ≈ = ∑ ( ) ξη σΔ 1 (积零为整, 得曲顶柱体体积之近似值) (4)、为得到V 的精值,只需让这 n 个小区域越来越小,即让每个小区域向某点收 缩。为此,我们引入区域直径的概念: 一个闭区域的直径是指区域上任意两点距离的最大者。 所谓让区域向一点收缩性地变小,意指让区域的直径趋向于零。 设n 个小区域直径中的最大者为λ , 则 V f n ii i i = → = lim ( ) ∑ , λ ξη σ 0 1 Δ

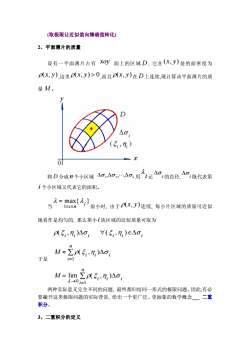
（取极限让近似值向精确值转化）2、平面薄片的质量设有一平面薄片占有xoy面上的区域D，它在(x,y)处的面密度为p(x,J),这里P(x,y)>0,而且P(x,y)在D上连续,现计算该平面薄片的质量M。yDA0,5nXo2.AaAo将D分成n个小区域Ao,Ao，Ao，用i记i的直径i既代表第i个小区域又代表它的面积。A= max(a,)很小时，由于P(x,J)连续，每小片区域的质量可近似当1<i≤n地看作是均匀的，那么第小i块区域的近似质量可取为p(5,n,)Ao)V(5,,n,)eAo;nM~ Zp(5,n,)Ao;i=1于是nM= lim Zp(5,,1nAg1-→0=1两种实际意义完全不同的问题，最终都归结同一形式的极限问题。因此有必要撇开这类极限问题的实际背景，给出一个更广泛、更抽象的数学概念二重积分。3、二重积分的定义

(取极限让近似值向精确值转化) 2、平面薄片的质量 设有一平面薄片占有 xoy 面上的区域 D , 它在 (, ) x y 处的面密度为 ρ(, ) x y ,这里 ρ(, ) x y > 0,而且 ρ(, ) x y 在 D 上连续,现计算该平面薄片的质 量 M 。 将 D 分成 n 个小区域 Δσ Δσ Δσ n , , , 1 2 " 用 λ i记 i Δσ 的直径, i Δσ 既代表第 i 个小区域又代表它的面积。 当 λ = λ ≤ ≤ max{ } 1 i n i 很小时, 由于 ρ(, ) x y 连续, 每小片区域的质量可近似 地看作是均匀的, 那么第小i 块区域的近似质量可取为 ρ(,) (,) ξ η σ ξ η σ ii i ii i Δ ∀ ∈Δ 于是 M ii i i n ≈ = ∑ ρξ η σ (,)Δ 1 M ii i i n = → = lim ( , ) ∑ λ ρξ η σ 0 1 Δ 两种实际意义完全不同的问题, 最终都归结同一形式的极限问题。因此,有必 要撇开这类极限问题的实际背景, 给出一个更广泛、更抽象的数学概念_ 二重 积分。 3、二重积分的定义

设(x,J)是闭区域D上的有界函数，将区域D分成个小区域Aoi,Ao2,"",Aon,2其中：Aαi既表示第i个小区域，也表示它的面积，i表示它的直径。A= max(a,)l<i<nV(5),n,)eA0;f(5,n,)Ao,(i=1,2,.,n)作乘积≥f(5,n,)A0;i=1作和式nlim f(5,n,)A存在,则称此极限值为函数f(x,J)在区域2→0i=1若极限Jl f(x, y)doD上的二重积分,记作DJJ f(x, y)do = lim Z f(5,n,)Ao;0;=1D即其中：f(x,y)称之为被积函数，f(x,y)do称之为被积表达式,do称之为面积元素，X，Y称之为积分变量,D称之为积分区域，≥f(5, n,)/0,i=l称之为积分和式。4、几个注意事项(1)、二重积分的存在定理若J(x,J)在闭区域D上连续，则F(x,J)在D上的二重积分存在。声明：在以后的讨论中,我们总假定在闭区域上的二重积分存在

设 f (, ) x y 是闭区域 D上的有界函数, 将区域 D分成个小区域 ΔΔ Δ σ 1 2 , , σ " σ n , 其中: Δσ i既表示第i 个小区域, 也表示它的面积, λ i表示它的直径。 λ = λ ≤ ≤ max{ } 1 i n i ∀ ∈ (,) ξ η σ ii i Δ 作乘积 f in ii i ( , ) , , ξ η Δσ ( ) =1 2 " 作和式 f ii i i n (,) ξη σΔ = ∑ 1 若极限 lim ( , ) λ ξη σ → = ∑ 0 1 f ii i i n Δ 存在,则称此极限值为函数 f (, ) x y 在区域 D上的二重积分,记作 f x yd D (, ) ∫∫ σ 。 即 f x yd f D ii i i n ( , ) lim ( , ) ∫∫ = ∑ → = σ ξη σ λ 0 1 Δ 其中: f (, ) x y 称之为被积函数, f (, ) x y dσ 称之为被积表达式,dσ 称之为面积元素, x, y 称之为积分变量, D称之为积分区域, f ii i i n (,) ξη σΔ = ∑ 1 称之为积分和式。 4、几个注意事项 (1)、二重积分的存在定理 若 f (, ) x y 在闭区域 D上连续, 则 f (, ) x y 在 D上的二重积分存在。 声明:在以后的讨论中,我们总假定在闭区域上的二重积分存在

J f(x, y)doAo;(2)、D中的面积元素do象征着积分和式中的iyDdydax0dc由于二重积分的定义中对区域D的划分是任意的,若用一组平行于坐标轴的直线来划分区域D，那么除了靠近边界曲线的一些小区域之外，绝大多数的小区域都是矩形,因此,可以将do记作dxdy（并称dxdy为直角坐标系下的面积元JJ f(x, y)dxdy素),二重积分也可表示成为D(3)、若J(x,J)≥0,二重积分表示以J(x,J)为曲顶,以D为底的曲顶柱体的体积。二、二重积分的性质二重积分与定积分有相类似的性质1、【线性性质】JJ[α. f(x, y)+ β.g(x, y)]d = α Jj f(x, y)do + β- JJ g(x,y)]do.D其中:α,β是常数。2、【对区域的有限可加性】若区域D分为两个部分区域D,D2,则J f(x,y)do=JJ f(x, y)do + J f(x, y)do0DD2

(2)、 f x yd D (, ) ∫∫ σ 中的面积元素dσ 象征着积分和式中的Δσ i 。 由于二重积分的定义中对区域 D的划分是任意的,若用一组平行于坐标轴的 直线来划分区域 D,那么除了靠近边界曲线的一些小区域之外,绝大多数的小区 域都是矩形,因此,可以将 dσ 记作 dxdy (并称 dxdy 为直角坐标系下的面积元 素),二重积分也可表示成为 f x y dxdy D (, ) ∫∫ 。 (3)、若 f (, ) x y ≥ 0,二重积分表示以 f (, ) x y 为曲顶,以 D为底的曲顶柱体的 体积。 二、二重积分的性质 二重积分与定积分有相类似的性质 1、【线性性质】 ∫∫ ∫∫ [ ( , ) ( , )] ( , ) ( , )] α ⋅ +⋅ f xy gxy d f xyd gxy d β σ = α ⋅∫∫ σ + β ⋅ σ D D D 其中: α , β 是常数。 2、【对区域的有限可加性】 若区域 D分为两个部分区域 D1 2 , D ,则 f xyd f xyd f xyd D D D ∫∫ ∫∫ (, ) (, ) (, ) σ =∫∫ σ + σ 1 2

3、若在D上,J(x,J)=1,为区域D的面积,则α= J[ 1dα = [[ doDD几何意义：高为1的平顶柱体的体积在数值上等于柱体的底面积。4、若在D上,F(x,J)≤Q(x,J),则有不等式J f(x, y)dg≤ JJ p(x, y)do特别地,由于-(x,≤(,)≤(,)],有J (x,y)d≤J[ If(x,y)] do5、【估值不等式】设M与m分别是F(x,J)在闭区域D上最大值和最小值,是M的面积，则m-o≤[l f(x,y)do<M.o6、【二重积分的中值定理】设函数(x,J)在闭区域D上连续,C是D的面积,则在D上至少存在一点(,n),使得Jf(x,y)dg=f(5, n).I =[(x2 +4y2 +9)do的值,D是圆域×2+≤4。例1、估计二重积分解：求被积函数f(x,J)=x2+4y2+9在区域D上可能的最值af=2x=0axaf=8y=0ay(0,0)是驻点,且(0,0)=9

3、若在 D 上, f (, ) x y ≡1,σ 为区域 D 的面积,则 σ = = ∫∫ ∫∫ 1d d σ σ D D 几何意义: 高为1的平顶柱体的体积在数值上等于柱体的底面积。 4、若在 D上, f (, ) (, ) x y ≤ϕ x y ,则有不等式 ∫∫ ∫∫ ≤ D D f (x, y)dσ ϕ(x, y)dσ 特别地,由于− f (x, y) ≤ f (x, y) ≤ f (x, y) ，有 f x y dσ f x y dσ D D ∫∫ ∫∫ ( , ) ≤ ( , ) 5、【估值不等式】 设 M 与m分别是 f (, ) x y 在闭区域 D上最大值和最小值,σ 是 M 的面积, 则 ∫∫ ⋅ ≤ ≤ ⋅ D m σ f (x, y)dσ M σ 6、【二重积分的中值定理】 设函数 f (, ) x y 在闭区域 D 上连续,σ 是 D 的面积,则在 D 上至少存在一 点(,) ξ η ,使得 ∫∫ = ⋅ D f (x, y) dσ f ( ξ,η ) σ 例 1、估计二重积分 = ∫∫ + + D I (x 4y 9)dσ 2 2 的值, D是圆域 x y 2 2 + ≤ 4 。 解: 求被积函数 9 ( , ) 4 2 2 f x y = x + y + 在区域 D上可能的最值 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = = = 8 0 2 0 y y f x x f ∂ ∂ ∂ ∂ (,) 0 0 是驻点,且 f (,) 00 9 = ；

在边界上,(x,J)= x2 + 4(4 - x3)+ 9 = 25 - 3x(-2 ≤x≤2)13≤f(x,y)≤25Jmax =25, min = 9,于是有36元=9.4元≤1≤25.4元=100元例2、设D为圆域x+R，求二重积分R-x-dD解：z=/R2-x?-y2是上半球面，由二重积分的几何意义可知，上述积分等于上半球体的体积：2元RJJ R-x-'do=-3例3、比较积分I,=[[in(x+y)da，,=[[(x+y)"do，I,=[[(x+y)do的大小,DD其中D是由直线x=0.y=0.x+y=和x+y=1所围成的。2解：因为积分域D在直线x+y=1的下方，所以对任意点(x,J)eD，均有1≤x+y≤1，从而有x+y≥(x+y)2>0，而ln(x+y)<0，故由二重积分的2性质得,≤1≤13。例4、判断（In(x2+y)dxdy的正负号。rsx+by/s1解：当rx|+lyk1时，0<x +y ≤(Ix/+/yD2 ≤1故In(x +y°)≤0又当In(x? +y)<0Ix|+lyk1于是( In(x? + y°)dxdy<0rs1311s1例5、不作计算，估计I={[er+)da的值，其中D是椭圆闭区域：x?≤1,(0<b<a)Ob2

在边界上, ( , ) 4(4 ) 9 25 3 ( 2 2) 2 2 2 f x y = x + − x + = − x − ≤ x ≤ 13 ≤ f (x, y) ≤ 25 25 max f = , 9 min f = , 于是有 36π =9⋅ 4π ≤I ≤25⋅ 4π =100π 例 2、设 D 为圆域 22 2 x + ≤ y R ，求二重积分 222 d D Rxy − − σ ∫∫ 。 解： 222 z Rxy = −− 是上半球面， 由二重积分的几何意义可知，上述积分等于上半球体的体积： 222 3 2 d 3 D R −− = xy R σ π ∫∫ 例 3、比较积分 ∫∫ = + D I1 ln(x y)dσ ， ∫∫ ∫∫ = + = + D D I (x y) dσ, I 3 (x y)dσ 2 2 的大小， 其中 D 是由直线 2 1 x = 0, y = 0, x + y = 和 x + y = 1所围成的。 解：因为积分域 D 在直线 x + y = 1的下方，所以对任意点(x, y) ∈ D ，均有 1 2 1 ≤ x + y ≤ ，从而有 ( ) 0 2 x + y ≥ x + y > ，而ln(x + y) < 0，故由二重积分的 性质得 1 2 3 I ≤ I ≤ I 。 例 4、判断 2 2 ||||1 ln( )d d rx y x y xy ≤+≤ + ∫∫ 的正负号。 解：当rx y ≤+< | | | |1时， 22 2 0 (| | | |) 1 <+≤ + ≤ xy x y 故 2 2 ln( ) 0 x y + ≤ 又当 | | | |1 x y + < 2 2 ln( ) 0 x y + < 于是 2 2 ||||1 ln( )d d 0 rx y x y xy ≤+≤ + < ∫∫ 例 5 、不作计算，估计 2 2 ( )d x y D I e σ + = ∫∫ 的值，其中 D 是椭圆闭区域： 2 2 2 2 1,(0 ) x y b a a b + ≤ <<

解：区域D的面积α=αb元在D上，0≤x2+?≤a?..1=e°<er+y'<e?g≤ [[e(r+y)dg≤g-eDab元 ≤ [[e(r+)dg ≤abre'D1.r例6、求lim-f(x,y)do-0元ptsp解：利用积分中值定理，即得：J f(x, )dg= f(5,n) J do= p"f(5,n)x?+y"sp?Y+y'sp?其中点(,n)是圆域x2+y≤p2内的一点。显然，当p→0时，点（5n)→(0,0）由函数的连续性知1rlim-f(x,y)da=lim f(,n)= f(0,0)p-0元p20-x*+y≤p?小结二重积分的定义（四步：分割、取近似、求和、取极限）二重积分的几何意义（曲顶柱体的体积）二重积分的性质（注意对称性质的用法）作业教材

解：区域 D 的面积σ = abπ 在 D 上， 222 ∵0 ≤ x + ≤ y a 22 2 0 1 x y a ee e + ∴ =≤ ≤ 22 2 ( )d x y a D σ σσ e e + ≤ ≤⋅ ∫∫ 22 2 ( )d x y a D ab e ab e π σ π + ≤ ≤ ∫∫ 例 6、求 222 2 0 1 lim ( , )d x y f xy ρ ρ σ → πρ + ≤ ∫∫ 解：利用积分中值定理，即得： 222 222 2 ( , )d ( , ) d ( , ) xy xy f xy f f ρ ρ σ ξ η σ πρ ξ η +≤ +≤ =⋅ = ∫∫ ∫∫ 其中点(,) ξ η 是圆域 22 2 x y + ≤ ρ 内的一点。 显然，当 ρ → 0时，点( , ) 0,0 ξ η → ( ) 由函数的连续性知 ( ) 222 2 0 0 1 lim ( , )d lim ( , ) 0,0 x y f xy f f ρ ρ ρ σ ξη → → πρ + ≤ = = ∫∫ 小结 二重积分的定义（四步：分割、取近似、求和、取极限） 二重积分的几何意义（曲顶柱体的体积） 二重积分的性质（注意对称性质的用法） 作业 教材

89.2二重积分的计算法教学目的：熟练掌握二重积分的计算方法教学重点：利用直角坐标和极坐标计算二重积分教学难点：化二重积分为二次积分的定限问题教学内容：利用二重积分的定义来计算二重积分显然是不实际的，二重积分的计算是通过两个定积分的计算（即二次积分）来实现的。一、利用直角坐标计算二重积分JJ f(x,y)do我们用几何观点来讨论二重积分D的计算问题。讨论中,我们假定 (x,J)≥0假定积分区域D可用不等式α≤x≤b(x)≤≤(x)表示,其中(x),2(x)在[a,b]上连续。JyIy=Φ2(αx)y=Φ,(x)y=(x)y=Φ(x)obbxoaxaJJ f(x, y)do的值等于以D为底,以曲面据二重积分的几何意义可知，Dz= f(x,y)为顶的曲项柱体的体积

§9.2 二重积分的计算法 教学目的：熟练掌握二重积分的计算方法 教学重点：利用直角坐标和极坐标计算二重积分 教学难点：化二重积分为二次积分的定限问题 教学内容： 利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通 过两个定积分的计算(即二次积分)来实现的。 一、利用直角坐标计算二重积分 我们用几何观点来讨论二重积分 f xyd D ∫∫ (, ) σ 的计算问题。 讨论中,我们假定 f (, ) x y ≥ 0 ； 假定积分区域 D可用不等式 axb x ≤ ≤ ϕ ≤ y ≤ ϕ x 1 2 () ()表示, 其中ϕ1( ) x , ϕ 2( ) x 在[,] a b 上连续。 据二重积分的几何意义可知, f xyd D ∫∫ (, ) σ 的值等于以 D 为底,以曲面 z = f (, ) x y 为顶的曲顶柱体的体积

z= f(x,y)92(x)= (@(x)1Ab0axox在区间[α,b]上任意取定一个点o,作平行于yoz面的平面x=xo,这平面截曲顶柱体所得截面是一个以区间[(x),P2(x)为底,曲线z=f(xo,)为曲边的曲边梯形，其面积为P2(x0)A(x。)=J f(xo,y)dy1(xo)一般地,过区间[a,b]上任一点x且平行于yo2面的平面截曲顶柱体所得截面的面积为P2(x)A(x)=J f(x, y)dyPi(x)利用计算平行截面面积为已知的立体之体积的方法，该曲顶柱体的体积为[02(x)bJ f(x, y)dy dxV = A(x)dx =Jaa;(x)从而有[2(t)J f(x, y)do =[J f(x, y)dy dx71a (x)(1)

在区间[,] a b 上任意取定一个点 x0 ,作平行于 yoz 面的平面 x x = 0 ,这平面 截曲顶柱体所得截面是一个以区间[ ( ), ( )] ϕ10 20 x x ϕ 为底,曲线 z = f ( ,) x y 0 为曲边的曲边梯形,其面积为 A x f x y dy x x ( ) ( ,) ( ) ( ) 0 0 1 0 2 0 = ∫ ϕ ϕ 一般地,过区间[,] a b 上任一点 x 且平行于 yoz 面的平面截曲顶柱体所得截 面的面积为 A x f x y dy x x () (, ) ( ) ( ) = ∫ ϕ ϕ 1 2 利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为 V Ax a dx f x y dy dx b x x a b = = ⎡ ⎣ ⎢ ⎢ ⎤ ⎦ ⎥ ⎥ ∫ ∫ ∫ () (, ) ( ) ( ) ϕ ϕ 1 2 从而有 f x y d f x y dy dx b a x x D ∫∫ ∫ ∫ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ( ) 2 ( ) 1 ( , ) ( , ) ϕ ϕ σ (1)