《高等数学》课程教学资源（PPT课件）第二章导数与微分_第四节隐函数及由参数方程所确定的函数的导数、相关变化率

第四节隐函数及参数方程所确定函数的导数 一、隐函数的导数 二、由参数方程所确定的函数的导数 三、相关变化率 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 一、隐函数的导数 二、由参数方程所确定的函数的导数 三、相关变化率

第四节隐函数及参数方程所确定函数的导数 一、隐函数的导数 1.定义 定义由y=f心)表示的函数称为显函数，其特点是 法则f为已知，即对定义域内的任一x，通过该法则可 计算出相应的y;二元方程F化，)=0在一定的条件下 能确定一个以x为自变量以y为因变量的函数，称之为 隐函数。如果能从方程F心，y)=0中解出因变量y,则 称该隐函数能显化 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 一、隐函数的导数 1. 定义 定义 由 y = f (x) 表示的函数称为显函数，其特点是 法则 f 为已知，即对定义域内的任一 x ，通过该法则可 计算出相应的 y ; 二元方程 F(x , y) = 0 在一定的条件下 能确定一个以 x 为自变量以 y 为因变量的函数，称之为 隐函数．如果能从方程 F(x , y) = 0 中解出因变量 y，则 称该隐函数能显化

第四节隐函数及参数方程所确定函数的导数 例如， y=sin x,y=Inx+v1-x2,y=vxInxv1-sin x 都是显函数、 方程x+y-1=0能确定一个隐函数y=y),它能显 化：y=1-x 方程y°+3x2y2+5x4-12=0能确定一个隐函数y=y) 但它不能显化. 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 例如， y = sin x , ln 1 , 2 y = x + − x y = x ln x 1− sin x 都是显函数. 方程 1 0 3 x + y − = 能确定一个隐函数 y = y(x)，它能显 化： 1 . 3 y = − x 方程 3 5 12 0 5 2 2 4 y + x y + x − = 能确定一个隐函数y = y(x) 但它不能显化

第四节隐函数及参数方程所确定函数的导数 2.隐函数的图形 二元方程Fx,y)=0所确定的一元隐函数的图形比 一元显函数的图形更复杂更漂亮 大学数学 网 域 数字化教学资源研发中心 全国高等学校教学研究中心 武汉纺织大学共建 网 sin25x-§ sin2y+sin xsin 5y=0 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 2. 隐函数的图形 二元方程 F(x , y) = 0 所确定的一元隐函数的图形比 一元显函数的图形更复杂更漂亮. sin 5 sin 2 sin sin 5 0 2 2 x − y + x y =

第四节隐函数及参数方程所确定函数的导数 8g (x2+y2)2 2xy =1 sin 40xv 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 1 sin 40 2 ( ) 2 2 2 + − = x y x y x y

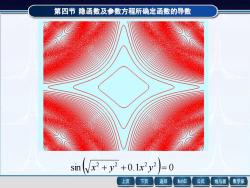
第四节隐函数及参数方程所确定函数的导数 sin Nx2+y2+0.1x2y2=0 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 sin ( 0.1 ) 0 2 2 2 2 x + y + x y =

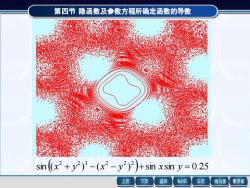
第四节隐函数及参数方程所确定函数的导数 sin ((x2+y2)3-(x2-y2)2)+sin xsin y=0.25 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 sin (( ) ( ) ) sin sin 0.25 2 2 3 2 2 2 x + y − x − y + x y =

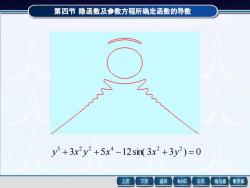
第四节隐函数及参数方程所确定函数的导数 y5+3x2y2+5x4-12sn(3x2+3y2)=0 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 3 5 12sin( 3 3 ) 0 5 2 2 4 2 2 y + x y + x − x + y =

第四节隐函数及参数方程所确定函数的导数 3.隐函数的求导方法 由二元方程Fx,y)=0所确定的隐函数y=y)的 导数的计算方法： 方程Fx,)=0两边对自变量x求导，因为y=yx) 是x的函数，所以在求导时，把y当成中间变量，利用 复合函数的求导法则求导.求导后得到一个关于一阶导 数的方程，解之即可. 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 3. 隐函数的求导方法 由二元方程 F(x , y) = 0 所确定的隐函数 y = y(x) 的 导数的计算方法： 方程 F(x , y) = 0 两边对自变量 x 求导，因为 y = y(x) 是 x 的函数，所以在求导时，把 y 当成中间变量，利用 复合函数的求导法则求导. 求导后得到一个关于一阶导 数的方程，解之即可

第四节隐函数及参数方程所确定函数的导数 例1求由方程+y-e=0所确定的隐函数的导数 dy 解 例2求由方程y+2y-x-3x?=0所确定的隐函数在 x=0处的导数 解 例3求椭圆 +】在点处的切线方程 解 上页 下页 返回 MathGS 公式 线与面 数学家

第四节 隐函数及参数方程所确定函数的导数 例1 求由方程e x + xy – e = 0所确定的隐函数的导数 第四节 隐函数及参数方程所确定函数的导数 解 例1 求由方程e y + xy – e = 0所确定的隐函数的导数 . d d x y 方程两边对 x 求导，得0 , d d d d e + + = x y y x x y y 解之得 ( e 0) . d e d +  + = − y y x x y x y x y O . d d x y 例2 求由方程 2 3 0 5 7 y + y − x − x = 所确定的隐函数在 x = 0 处的导数 . d d x=0 x y 第四节 隐函数及参数方程所确定函数的导数 解 例2 求由方程 2 3 0 5 7 y + y − x − x = 所确定的隐函数在 x = 0 处的导数 . d d x=0 x y 方程两边对 x 求导，得 1 21 0 , d d 2 d d 5 4 6 + − − x = x y x y y 解之得 . 5 2 21 1 d d 4 6 + + = y x x y 因为当 x = 0 时，y = 0，所以 . 2 1 d d 0 = x= x y x y O 例3 求椭圆 1 2 2 2 2 + = b y a x 在点(x0 , y0 ) 处的切线方程. 第四节 隐函数及参数方程所确定函数的导数 解 例3 求椭圆 1 2 2 2 2 + = b y a x 在点(x0 , y0 ) 处的切线方程. 在椭圆方程两边对 x 求导，得 0 , 2 2 2 2 =  + b yy a x 解之得 . 2 2 a y b x y  = − 于是切线斜率为 | , 0 2 0 2 ( , ) 0 0 a y b x k y =  x y = − 切线方程为 ( )0 0 2 0 2 0 x x a y b x y − y = − − 1. 2 0 2 0 + = b y y a x x