《高等数学》课程教学资源（PPT课件）第一章函数与极限_第三节函数的极限

第三节函数的极限 函数极限的定义 二、函数极限的性质 上页 下页 返回 MathS 公式 线与面 数学家

第三节 函数的极限 一、函数极限的定义 二、函数极限的性质

第三节函数的极限 函数极限的定义 在上一节我们讨论了数列的极限，而数列xm=f() 可以看成是函数y=fx)当自变量x取正整数的特殊情 形.所以，可以用研究数列极限完全相同的思想和方法 来研究函数在自变量的某一变化过程中，函数值的变化 情况，即函数的极限.自变量的变化过程主要有两种： ()自变量趋于有限值(cx): (2)自变量趋于无穷大(x-→∞) 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 一、函数极限的定义 在上一节我们讨论了数列的极限，而数列 xn = f (n) 可以看成是函数 y = f (x) 当自变量x 取正整数的特殊情 形. 所以，可以用研究数列极限完全相同的思想和方法 来研究函数在自变量的某一变化过程中，函数值的变化 情况，即函数的极限. 自变量的变化过程主要有两种： (1) 自变量趋于有限值(x→x0 )； (2) 自变量趋于无穷大(x→)

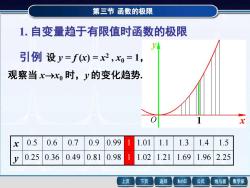
第三节函数的极限 1.自变量趋于有限值时函数的极限 引例设y=fc)=x2,x=1, 观察当xx时，y的变化趋势. 0.5 0.6 0.7 0.9 0.99 1 1.01 1.1 1.3 1.4 1.5 0.25 0.36 0.49 0.81 0.98 1.02 1.21 1.69 1.96 2.25 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 1. 自变量趋于有限值时函数的极限 x y O 1 1.96 1.4 y 0.25 0.36 0.49 0.81 0.98 1 1.02 1.21 1.69 2.25 x 0.5 0.6 0.7 0.9 0.99 1 1.01 1.1 1.3 1.5 引例 设 y = f (x) = x 2 , x0 = 1， 观察当 x→x0 时，y 的变化趋势

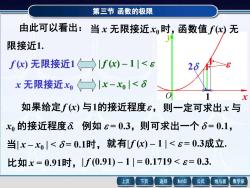
第三节函数的极限 由此可以看出：当x无限接近xo时，函数值fx)无 限接近1. fc)无限接近1)f)-1|< x无限接近xIx-|<6 如果给定fx)与1的接近程度ε，则一定可求出x与 o的接近程度6.例如￡=0.3，则可求出一个6=0.1， 当|x-x|<6=0.1时，就有fc)-1<e=0.3成立. 比如x=0.91时，1f(0.91)-1|=0.1719<8=0.3. 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 则一定可求出 x 与 x y O 1  2 由此可以看出： 当 x 无限接近 x0 时，函数值 f (x) 无 限接近1. f (x) 无限接近1 | f (x) – 1 | <  x 无限接近 x0 | x – x0 | <  如果给定 f (x) 与1的接近程度， x0 的接近程度. 例如  = 0.3，则可求出一个  = 0.1， 当| x – x0 | <  = 0.1时，就有| f (x) – 1 | <  = 0.3成立. 比如 x = 0.91时，| f (0.91) – 1 | = 0.1719 <  = 0.3. 则一定可求出 x 与

第三节函数的极限 定义1设函数f)在点的某一去心邻域内有定 义.如果存在常数A,对于任意给定的正数ε（不论它 多么小)，总存在正数δ，使得当x满足不等式 0<|x-xo|<6 时，对应的函数值f)都满足不等式 1f)-A|<6, 那么常数A就叫做函数fc)当x→x时的极限，记作 lim(x)=A或f)→A(当x→x). x→x0 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 定义1 设函数 f (x) 在点 x0 的某一去心邻域内有定 义．如果存在常数 A，对于任意给定的正数  (不论它 多么小)，总存在正数  ，使得当 x 满足不等式 0 < | x – x0 | <  时，对应的函数值 f (x) 都满足不等式 | f (x) – A | <  ， 那么常数 A 就叫做函数 f (x) 当 x → x0 时的极限，记作 f x A x x = → ( ) lim 0 或 f (x) → A (当 x → x0 )

第三节函数的极限 注意 定义中的00,36>0,当0<|x-x0l<6时， 有 lfx)-A|<6. 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 注意 定义中的 0 0，  > 0，当 0 < | x – x0 | <  时， 有 | f (x) – A | < 

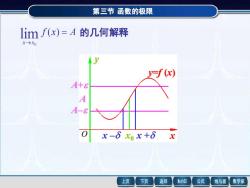
第三节函数的极限 limf(x)=A的几何解释 x→x0 y=f(x) A+6 A A-8 x-δx0+6x 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 f x A x x = → ( ) lim 0 的几何解释 A– A+ A x – x0 x + y=f (x) x y O

第三节函数的极限 例1证明limc=c(c为常数). x→x0 证明之 例2证明limx=x。: x→X0 证明 例3证明lim(3x-1)=2 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 例1 第三节 函数的极限 证明 例1 证明 c c x x = → lim 0 (c 为常数). 因为 | f (x) − A|=| c − c |= 0 , 所以，  > 0，可任取  > 0，当 0 0，总可取  =  ，当 0 0，可取 则当 0 < | x – 1 | <  时， 能使不等式 成立. 因此 (3 1) 2 . lim 1 − = → x x = 3| x −1| , 为了使 | f (x) − A|  , 只要 . 3 | 1|  x −  , 3   = | f (x) − A| =| (3x −1) − 2 |  (3 1) 2 . lim 1 − = → x x

第三节函数的极限 例4证明 x2-1 limx- 2 x-1 证明 例5证明：当o>0时，lim=Vx 证明之 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 例4 证明 2 . 1 1 2 1 lim = − − → x x x 第三节 函数的极限 证明 因为 | f (x) − A| 2 1 1 2 − − − = x x 所以，  > 0，可取 则当 0 0 时， . lim 0 0 x x x x = → 第三节 函数的极限 证明 因为 | f (x) − A| 0 = x − x 所以，  > 0，要使 0 0 x x x x + − = 例5 证明：当 x0 > 0 时， . lim 0 0 x x x x = → , | | 0 0 x x − x  | f (x) − A|  , 只要  0 0 | x − x | x 且 x  0，而 x  0 可用 | x – x0 |  x0 保证，因此取 min  , , 0 0  = x x  则当 0 < | x – x0 |   时，就有 . 0 x − x   所以 . lim 0 0 x x x x = →

第三节函数的极限 左极限与右极限 一→X0 「xx0且x→x0,记作x>x 左极限 f(xo)=limf(x)=4 x→x0 V8>0,36>0, 当0-6<x<0时， 有 lfx)-A|<6. 上页 下页 返回 MathGS 公式 线与面 数学家

第三节 函数的极限 左极限与右极限 x→x0 x x0 x x x x0 且 x→x0 , 记作 x→x0 + f x f x A x x = = − → − ( ) ( ) lim 0 0   > 0，  > 0，当 x0 –  < x < x0 时， 有 | f (x) – A | <  . 左极限