《高等数学》课程教学资源（PPT课件）第三章微分中值定理与导数的应用_第一节微分中值定理

第一节微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 上页 下页 返回 MathS 公式 线与面 数学家

第一节 微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理

第一节微分中值定理 一、罗尔定理 1.几何发现 X2 X3( X x 如图所示的曲线，在x1一x6这6个相应点处有水平切 线，这6点均是曲线在局部的最高点或最低点.那么如 何用分析语言来描述这一几何现象呢？ 上页 下页 返回 MathGS 公式 线与面 数学家

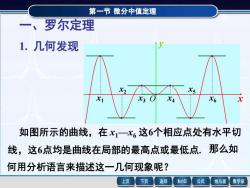
第一节 微分中值定理 一、罗尔定理 1. 几何发现 如图所示的曲线，在 x1—x6 这6个相应点处有水平切 线，这6点均是曲线在局部的最高点或最低点. 那么如 何用分析语言来描述这一几何现象呢？ x1 x2 x3 x4 x5 x6 x y O

第一节微分中值定理 X> X3( 首先设曲线的方程为y=fx),曲线在x=x相应点处 有水平切线，则函数y=fx)在x=x处可导，且f'比1)=0， x=x相应点是曲线的局部最高点，即在x1的某一邻域 内有fx)≤fc).最后理清条件与结论的关系即得 上页 下页 返回 MathGS 公式 线与面 数学家

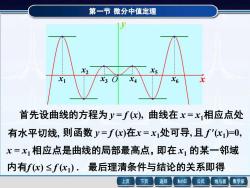
第一节 微分中值定理 首先设曲线的方程为 y = f (x), 曲线在 x = x1相应点处 有水平切线, 则函数 y = f (x)在x = x1处可导, 且 f (x1 )=0, x = x1 相应点是曲线的局部最高点，即在 x1 的某一邻域 内有f (x)  f (x1 ) . 最后理清条件与结论的关系即得 x1 x2 x3 x4 x5 x6 x y O

第一节微分中值定理 2.费马引理 费马引理设函数fx)在点x的某邻域U心o)内有 定义，并且在xo处可导，如果对任意的x∈Uc),有 fx)≤fco)(或f)≥fc), 那么f')=0. 证明O 通常称导数等于零的点为函数的驻点 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 微分中值定理 2. 费马引理 费马引理 设函数 f (x) 在点 x0 的某邻域 U(x0 ) 内有 定义，并且在 x0 处可导，如果对任意的 x  U(x0 )，有 f (x)  f (x0 ) (或 f (x)  f (x0 ))， 那么 f (x0 ) = 0 . 第一节 微分中值定理 证明 费马引理 设函数 f (x) 在点 x0 的某邻域 U(x0 ) 内有 定义，并且在 x0 处可导，如果对任意的 x  U(x0 )，有 f (x)  f (x0 ) (或 f (x)  f (x0 ))， 那么 f (x0 ) = 0 . 不妨设 x  U(x0 ) 时，f (x)  f (x0 )， 则在该邻 内恒有 f (x) – f (x0 )  0 . f (x0 ) = 0 f (x0 )  0 且 f (x0 )  0 下面用左右导数来证明. 通常称导数等于零的点为函数的驻点

第一节微分中值定理 3.罗尔定理 费马引理的结论非常好，但不太好用.有时需要快 速地判别一条曲线在一个指定的区间上是否有水平切线 用费马引理就是要判别曲线是否有局部最高（低）点，且 函数在这点是否可导，而这有时是困难的.因此我们希 望将费马定理的条件进行改造，使之更好用.那么如何 改造呢？我们还是从几何上来找线索 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 微分中值定理 3. 罗尔定理 费马引理的结论非常好，但不太好用. 有时需要快 速地判别一条曲线在一个指定的区间上是否有水平切线 用费马引理就是要判别曲线是否有局部最高(低)点，且 函数在这点是否可导，而这有时是困难的．因此我们希 望将费马定理的条件进行改造，使之更好用. 那么如何 改造呢？我们还是从几何上来找线索

第一节微分中值定理 如图所示，曲线y=f(x) 在开区间(a,b)内有 D 5条水平切线，并且 它们都平行于弦AB. 那么这条曲线在a,b] 到底满足了哪些条件才做到了这一点呢？从图可以看 出：()它是连续曲线；(2)除两个端点外处处有切线； (3)f(@)=f(b).下面我们会证明任意曲线只要在一个 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 微分中值定理 a b A B x y O 如图所示，曲线 y = f (x) 在开区间 (a , b) 内有 5条水平切线，并且 它们都平行于弦AB. 那么这条曲线在[a , b] 到底满足了哪些条件才做到了这一点呢？ 从图可以看 出：(1) 它是连续曲线；(2) 除两个端点外处处有切线； (3) f (a) = f (b) . 下面我们会证明任意曲线只要在一个

第一节微分中值定理 (1)它是连续曲线；(2)除两个端点外处处有切线； (3)f(@=f(b). 闭区间上满足上述三个条件，则在相应的开区间内一定 有水平切线 把上述用几何语言描述的条件和结论用分析语言描 述出来就是下面的罗尔定理 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 微分中值定理 (1) 它是连续曲线；(2) 除两个端点外处处有切线； (3) f (a) = f (b) . 闭区间上满足上述三个条件，则在相应的开区间内一定 有水平切线. 把上述用几何语言描述的条件和结论用分析语言描 述出来就是下面的罗尔定理

第一节微分中值定理 罗尔定理如果函数f()满足 (1)在闭区间[a,b]上连续； (2)在开区间(a,b)内可导； (3)在区间端点处的函数值相等，即f(侧=f(b), 那么在(a,b)内至少存在一点5，使得 f'(5)=0. 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 微分中值定理 罗尔定理 如果函数 f (x) 满足 (1) 在闭区间 [a , b] 上连续； (2) 在开区间 (a , b) 内可导； (3) 在区间端点处的函数值相等，即 f (a) = f (b)， 那么在 (a , b) 内至少存在一点  ，使得 f ( ) = 0 . 第一节 微分中值定理 证明 (1) 在闭区间 [a , b] 上连续；(2) 在开区间 (a , b) 内可导； (3) f (a) = f (b)， 因为 f (x) 在闭区间 [a , b] 上连续，根据在闭 区间上连续函数的最大值最小值定理，f (x) 在 [a , b] 上 一定取得最大值 M 和最小值 m . 分两种情形讨论： (1) M = m . 因为只有常数函数的最大值与最小值相 等，故在闭区间 [a , b] 上 f (x) = M，于是 f (x) = 0 . 因而此时结论成立

第一节微分中值定理 注意 罗尔定理是一个充分性定理，定理的条件不全满足 时，可能有该结论，也可能没有该结论.例如 f(x)=x3+x x2,0≤x<1 19 yh f(x)= 0,x=1 f(x)=x -1 0 1x fx)在0,1]不连续f)在(0,1)不可导 f(0)≠f(1) 上页 下页 返回 MathGS 公式 线与面 数学家

第一节 微分中值定理 注意 罗尔定理是一个充分性定理， 定理的条件不全满足 时，可能有该结论，也可能没有该结论. 例如 f (x) 在[0 , 1]不连续 f (x) 在(0 , 1)不可导 f (0)  f (1) x y 1    =   = 0, 1 , 0 1 ( ) 2 x x x f x O x y -1 1 3 2 f (x) = x O x y 1 f x = x + x 3 ( ) O

第一节微分中值定理 19 f(x)=x+2sin x f(x)=x+2sin x 2元x 2元x f(0)≠f(2π) f(0)≠f(2π)且不连续 上页 下页 返回 MathGS 公式 线与面 数学家

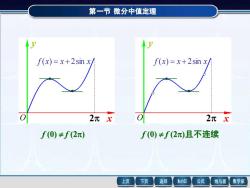
第一节 微分中值定理 x y f (x) = x + 2sin x f (0)  f (2) O 2 x y f (x) = x + 2sin x f (0)  f (2)且不连续 O 2