《高等数学》课程教学资源（PPT课件）第五章定积分_第二节微积分基本公式

第二节微积分基本公式 一、引例 二、积分上限的函数 三、牛顿莱布尼茨公式 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 一、引例 二、积分上限的函数 三、牛顿—莱布尼茨公式

第二节微积分基本公式 一、引例 设一物体作变速直线运动，其速度函数为（①，位置 函数为s(),求物体在时间间隔[T1,T2]内经过的路程， 路程s可以用两种方法计算： 用速度函数计算：s=) 第一节问题2 用位置函数计算：s=s(T)-s(T). 于是有 s=0)dt=s(T)-s), 在这时里有s'(t)=v(t),即s(是v()的一个原函数， 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 一、引例 设一物体作变速直线运动，其速度函数为 v(t)，位置 函数为 s(t) , 求物体在时间间隔 [T1 , T2 ] 内经过的路程. 路程 s 可以用两种方法计算： 用速度函数计算： ( )d ; 2 1  = T T s v t t 第一节问题2 用位置函数计算： ( ) ( ). 2 T1 s = s T −s 于是有 ( )d ( ) ( ) , 2 1 2 1 s v t t s T s T T T = = −  在这时里有 s (t) = v(t) , 即 s(t) 是 v(t) 的一个原函数

第二节微积分基本公式 v(t)dt =s(T)-s(T) 上式说明：定积分v)t等于被积函数在积分区 间[T1,T】上的一个原函数s)在积分区间上的增量. 那么这一结论具不具有普遍性呢？即若设Fx)是 fc)在区间[a,b]上的一个原函数，是否也有 f(x)dx=F(b)-F(a). 这就是本节要研究的问题， 上页 下页 返回 MathS 公式 线与面 数学家

第二节 微积分基本公式 ( )d ( ) ( ) 2 1 2 1 v t t s T s T T T = −  上式说明：  2 1 ( )d T T v t t 等于被积函数 v(t) 在积分区 间[T1 , T2 ] 上的一个原函数 s(t) 在积分区间上的增量. 那么这一结论具不具有普遍性呢？ 即若设 F(x) 是 f (x) 在区间 [a , b] 上的一个原函数，是否也有 f (x)dx F(b) F(a). b a = −  这就是本节要研究的问题. 定积分

第二节微积分基本公式 二、积分上限的函数及其导数 1.定义 定义设函数f)在区间[a,b]上连续，x∈[a,b, 则定积分f(t)dt是积分上限x的函数，称之为积分 上限的函数，记作x): Φ(x)=ft)dt(a≤x≤b) 下面来研究积分上限的函数的性质， 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 二、积分上限的函数及其导数 1. 定义 定义 设函数 f (x) 在区间 [a , b] 上连续，x  [a , b], 则定积分  x a f (t)dt 是积分上限 x 的函数，称之为积分 上限的函数， Φ(x) f (t)dt (a x b). x a =    下面来研究积分上限的函数的性质. 记作 (x)：

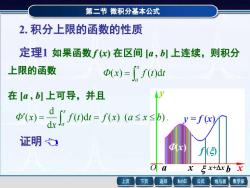
第二节微积分基本公式 2.积分上限的函数的性质 定理1如果函数fx)在区间[a,]上连续， 则积分 上限的函数 D(x)=["f(t)dr 在[a,b]上可导，并且 de0=wasrsh. y=f(c 证明 f( Ex+Axb x 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 a x  x+x b x y y = f (x) (x) f () O 2. 积分上限的函数的性质 定理1 如果函数 f (x) 在区间 [a , b] 上连续，则积分 上限的函数  = x a Φ(x) f (t)dt 在 [a , b] 上可导，并且 ( )d ( ) ( ). d d ( ) f t t f x a x b x Φ x x a  = =    第二节 微积分基本公式 证明 ( )d ( ) ( ) . d d ( ) [ , ], ( ) f t t f x a x b x f x C a b Φ x x a   = =    若 x  (a , b)，设 x 取得增量x, 且x+ x(a, b) 则 Φ(x) = Φ(x + x) −Φ(x)   = − + x a x x a f (t)dt f (t)dt  + = x x x f (t)dt = f ( )x . 积分中值定理 a x  x+x b x y y = f (x) (x) f () O

第二节微积分基本公式 定理2如果函数fw)在区间[a,b]上连续，则函数 (x)=[f(t)dr 就是f)在[a,b]上的一个原函数、 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 定理2 如果函数 f (x) 在区间 [a , b] 上连续，则函数  = x a Φ(x) f (t)dt 就是 f (x) 在 [a , b] 上的一个原函数

第二节微积分基本公式 三、牛顿一莱布尼茨公式 定理3如果函数Fx)是连续函数fx)在区间[a,b] 上的一个原函数，则 f()dx-F(6b)-F(a) 牛顿一莱布尼茨 公式 证明 牛顿一莱布尼茨公式也称微积分基本公式 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 三、牛顿—莱布尼茨公式 定理3 如果函数 F(x) 是连续函数 f(x) 在区间 [a , b] 上的一个原函数，则 f (x)dx F(b) F(a). b a = −  牛顿—莱布尼茨 公式 第二节 微积分基本公式 证明 由定理1知  = x a Φ(x) f (t)dt 也是 f (x) 在区间 [a , b] 上的一个原函数， 从而有 F(x) −Φ(x) = C (a  x  b). 在上式中令 x = a ，得 C = F(a)，于是上式变为 f (t)dt F(x) F(a) , x a = −  f (t)dt F(b) F(a) . b a = −  证毕 牛顿—莱布尼茨公式也称微积分基本公式

第二节微积分基本公式 例1计算第一节中的定积分xdx 解 2计牌小 dx 解 例3计算」： 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 例1 计算第一节中的定积分 d . 1 0 2  x x 第二节 微积分基本公式 解 例1 计算第一节中的定积分 d . 1 0 2  x x  1 0 2 x dx 1 0 3 3 1       = x . 3 1 例2 计算 . = 1 3 d 1  2 − + x x 第二节 微积分基本公式 解 例2 计算 . 1 3 d 1  2 − + x x − + 3 1 2 1 d x x   3 1 = arctan − x = arctan 3 − arctan(−1)       = − − 4 π 3 π . 12 7π = 例3 计算 . 1 d  2 − − x x 第二节 微积分基本公式 解 例3 计算 . 1 d  2 − − x x  − − 1 2 d x x   1 2 ln | | − = − x = ln 1− ln 2 = −ln 2

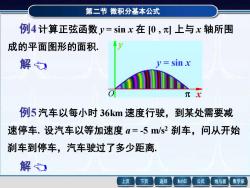
第二节微积分基本公式 例4计算正弦函数y=sinx在0，上与x轴所围 成的平面图形的面积。 解 V= sin x 例5汽车以每小时36km速度行驶，到某处需要减 速停车.设汽车以等加速度a=5m/s2刹车，问从开始 刹车到停车，汽车驶过了多少距离。 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 例4 计算正弦函数 y = sin x 在 [0 , ] 上与 x 轴所围 第二节 微积分基本公式 解 例4 计算正弦函数 y = sin x 在 [0 , ] 上与 x 轴所围 成的平面图形的面积. 所围成的图形如图所示. 它是曲边梯形的一个特例，由定 积分的几何意义，得  = π 0 A sin xdx   π 0 = − cos x = −cosπ+cos0 = 2 . x y y = sin x O  成的平面图形的面积. 例5 汽车以每小时 36km 速度行驶，到某处需要减 速停车. 设汽车以等加速度 a = -5 m/s2 刹车，问从开始 刹车到停车，汽车驶过了多少距离. 第二节 微积分基本公式 解 例5 汽车以每小时 36km 速度行驶，到某处需要减 速停车. 设汽车以等加速度 a = -5 m/s2 刹车，问从开始 刹车到停车，汽车驶过了多少距离. 设开始刹车的时刻为 t = 0，此时汽车的速度 v0 = 36 km/h = 10 m/s . 刹车后汽车减速行驶，其速度为 v(t) = v0 + at = 10 – 5t . 于是从开始刹车到停车所用时间为 10 – 5t = 0 t = 2s. 故所求距离为  = 2 0 s v(t)dt  = − 2 0 (10 5t)dt =10 (m) . x y y = sin x O 

第二节微积分基本公式 关于积分上限的函数的求导，不加证明地补充下面 几条公式： d)r (fo0）=-e （fod)=feoa （Cdf0）=fox》px)-fw》w 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 微积分基本公式 关于积分上限的函数的求导，不加证明地补充下面 几条公式： f (t)dt f (x) ; x a =         f (t)dt f (x) ; b x = −         ( )d ( ( )) ( ) ; ( ) f t t f x x x a    =          ( )d ( ( )) ( ) ( ( )) ( ). ( ) ( ) f t t f x x f x x x x       =  −         