《高等数学》课程教学资源（PPT课件）第四章不定积分_第二节换元积分法

第二节换元积分法 一、第一类换元积分法 二、第二类换元积分法 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 一、第一类换元积分法 二、第二类换元积分法

第二节换元积分法 一、第一类换元积分法 由第一节我们已知道，对应于一个求导公式，就有 一个积分公式，那么，对应于复合函数的求导法则，有 没有一个相应的积分法则呢？这就是下面的定理。 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 一、第一类换元积分法 由第一节我们已知道，对应于一个求导公式，就有 一个积分公式，那么，对应于复合函数的求导法则，有 没有一个相应的积分法则呢？ 这就是下面的定理

第二节换元积分法 定理1设函数f(0)具有原函数，u=p(),则有换 元公式 (x(x)dx=f(u)du =p(x) 证明 如何应用换元公式求「g(x)dx呢？ (①分解 g(x)=f(p(x)p'(x),这一步最难 (2)凑微分o'(x)x=dp(x)=du, (3)计算 「f(u)d. 要容易积出 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 定理1设函数 f (u) 具有原函数，u = (u) ，则有换 [ ( )] ( )d ( ( )d ) . u ( x) f x x x f u u      =  = 元公式 第二节 换元积分法 证明 设 F(u) 是 f (u) 的原函数，则有 F(u) = f (u) 或 f (u)du = F(u) +C .  根据复合函数求导法则，有 ( ( )d ) ( ( ( )) ) ( ) = +          = f u u F x C u x   = F((x))(x) = f ((x))(x). 证毕 如何应用换元公式求  g(x)dx 呢？ (1) 分解 g(x) = f ((x))(x) , (2) 凑微分 (x)dx = d(x) = du , (3) 计算 f (u)du .  这一步最难 要容易积出

第二节换元积分法 例1求「cos(2x+3r 例4求「xedx. 解 解 例2求 dx 例5求∫tanxdx 解 解 例3求 dx dx (a>0) 例6求 解 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 第二节 换元积分法 换元积分法 解 例1 求 cos(2x 3)dx .  + cos(2x 3)dx  + cos(2x 3) (2x 3) dx 2 1  = +  +   = cos(2 + 3)d(2 + 3) 2 1 x x 令u =2x+3  cosudu 2 1 = sin u +C 2 1 消去u sin(2 3) . 2 1 x + +C 联想到公式 x x = x +C  例1 求  cos(2x + 3)dx . cos d sin 第二节 换元积分法 解 例2 求 . d  2 2 a + x x 联想到公式 x C x x = + +  arctan 1 d 2  + 2 2 d a x x        + = 2 2 1 1 d a x x a x a x a a x d 1 1 1 2               + =              + =  a x a a x d 1 1 1 2 u a u d 1 1 1  2 + = u C a = arctan + 1 arctan . 1 C a x a = + 例2 求 . d  2 2 a + x x 第二节 换元积分法 解 例3 求 ( 0). d 2 2  −  a a x x 联想到 公式 x C x x = + −  arcsin 1 d 2  − 2 2 d a x x x a a x d 1 1 1  2        − =              − = a x a x d 1 1 2 arcsin C . a x = + 例3 求 ( 0). d 2 2  −  a a x x 第二节 换元积分法 解 例4 求 e d . 2 x x x  x x x e d 2  x x x e 2 d 2 1 2  =  e d( ) 2 1 2 2 x x  = e . 2 1 2 C x = + 例4 求 e d . 2 x x x  第二节 换元积分法 解 例5 求 tan xdx .  tan xdx  x x x d cos sin  =  = x x cos d(cos ) = ln | cos x | +C . 例5 求 tan xdx .  第二节 换元积分法 解 例6 求 . d  2 2 x − a x  − 2 2 d x a x x a x a x a d 1 1 2 1        + − − = d( ) 1 2 1 d( ) 1 2 1 x a a x a x a a x a + + − − − =   x a C a x a a = − − ln | + | + 2 1 ln | | 2 1 ln . 2 1 C x a x a a + + − = 例6 求 . d  2 2 x − a x

第二节换元积分法 例7求 dx 例10求sin4xdx. x(1+2nx) 解 解 例8求∫secxdx 例11求「sn2 cos'xdx 解 解 例9求sin3xdx 例12求∫sin2xcos4xdx 解 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 第二节 换元积分法 换元积分法 解 例7 求 . (1 2ln ) d  x + x x  (1+ 2ln ) d x x x  + = x x 1 2ln d(ln )  + = x x 1 2ln d(2ln ) 2 1  + + = x x 1 2ln d(1 2ln ) 2 1 ln |1 2ln | . 2 1 = + x +C 例7 求 . (1 2ln ) d  x + x x 第二节 换元积分法 解 例8 求 sec xdx .  sec xdx  x x d cos 1  = x x x d cos cos  2 = d(sin ) 1 sin 1 2 x x  − = C x x + − + = sin 1 sin 1 ln 2 1 ln sec tan . 2 1 = x + x +C 例8 求 sec xdx .  第二节 换元积分法 解 例9 求 sin d . 3 x x  sin x dx 3  sin x sin x dx 2  = (1 cos ) d(cos ) 2 x x  = − − cos . 3 1 cos 3 = − x + x +C 例9 求 sin d . 3 x x  第二节 换元积分法 解 例10 求 sin d . 4 x x  sin xdx 4  x x d 2 1 cos 2 2        − = (1 2cos 2x cos 2x)dx 4 1 2  = − + x x x d 2 1 cos 4 1 2cos 2 4 1        + = − + (3 4cos 2x cos 4x)dx 8 1  = − + sin 4 . 32 1 sin 2 4 1 8 3 = x − x + x +C 例10 求 sin d . 4 x x  第二节 换元积分法 解 例11 求 sin cos d . 2 5 x x x  sin x cos xdx 2 5  sin x cos x cos xdx 2 4  =  sin (1 sin ) d(sin ) 2 2 2 x x x  = − (sin 2sin sin ) d(sin ) 2 4 6 x x x x  = − + sin . 7 1 sin 5 2 sin 3 1 3 5 7 = x − x + x +C 例11求 sin cos d . 2 5 x x x  第二节 换元积分法 解 例12 求 sin cos d . 2 4 x x x  sin x cos x dx 2 4  (sin x cos x) cos x dx 2 2 2  = x x x d 2 1 cos 2 sin 2 2 1 2 +        =  (sin 2x sin 2x cos 2x) dx 8 1 2 2  = +   = − x x + sin 2x cos 2xdx 8 1 (1 cos 4 )d 16 1 2 sin 2 . 48 1 sin 4 64 1 16 1 3 = x − x + x +C 例12 求 sin cos d . 2 4 x x x 

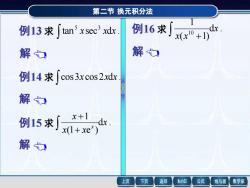
第二节换元积分法 例13求∫an3xsec3xdr 例16求 dx xx0+ 解 解 例14求∫cos3xcos2dr 解 例15求n0 dx 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 第二节 换元积分法 解 例13 求 tan sec d . 5 3 x x x  tan x sec xdx 5 3  tan x sec x sec xtan xdx 4 2 =   (sec 1) sec d(sec ) 2 2 2 x x x  = − (sec 2sec sec )d(sec ) 6 4 2 x x x x  = − + sec . 3 1 sec 5 2 sec 7 1 7 5 3 = x − x + x +C 例13 求 tan sec d . 5 3 x x x  第二节 换元积分法 解 例14 求 cos3x cos 2x dx.  cos3x cos 2x dx  (cos5x cos x) dx 2 1  = + sin . 2 1 sin 5 10 1 = x + x +C 例14 求 cos3x cos 2xdx .  第二节 换元积分法 解 例15 求 d . (1 e ) 1 x x x x  x + + x x x x x d (1 e ) 1  + + x x x x x x x d e (1 e ) ( 1)e  + + = d( e ) e (1 e ) 1 x x x x x x  + = d( e ) 1 e 1 e 1 x x x x x x        + = − x x C x x = ln | e | −ln |1+ e | + . 1 e e ln C x x x x + + = 例15 求 d . (1 e ) 1 x x x x  x + + 第二节 换元积分法 解 例16 求 d . ( 1) 1 10 x x x  + x x x d ( 1) 1  10 + x x x x d ( 1) 10 10 9  + = d( ) ( 1) 1 10 1 10 10 10 x x x  + = d( ) 1 1 1 10 1 10 10 10 x x x        + = − . 1 ln 10 1 10 10 C x x + + = 例16 求 d . ( 1) 1 10 x x x  +

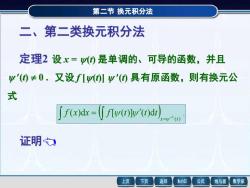
第二节换元积分法 二、第二类换元积分法 定理2设x=0是单调的、可导的函数，并且 少'（④≠0.又设f[)少'(）具有原函数，则有换元公 式 「fx)d=「fwow'()d 证明之 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 二、第二类换元积分法 定理2 设 x = (t) 是单调的、可导的函数，并且  (t)  0 . 又设 f [(t)]  (t) 具有原函数，则有换元公 式 ( )d ( [ ( )] ( )d ) . ( ) 1 x t f x x f t t t −   = =     第二节 换元积分法 证明 设 f [(t)] (t)的原函数为  (t) , 记  [-1 (x)] = F(x) , F(x) 证毕 利用复合函数及反函数的求导法则 x t t Φ d d d d =  ( ) 1 [ ( )] ( ) t f t t     =   = f [ (t)] = f (x) , 即F(x) 是 f (x) 的原函数

第二节换元积分法 例17求2-x2dr(a>0) 解 Va2-x2 18求 dx (a>0). +a 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 第二节 换元积分法 解 例17 求 d ( 0). 2 2 −   a x x a 令 x = asin t , , 2 π 2 π −  t  则 2 2 a − x a a t 2 2 2 = − sin = a cost , dx = a cost dt, a x dx 2 2  − a cost a cost dt  =  a cos t dt 2 2  = C t t a  +      = + 4 sin 2 2 2 t t C a t a = + sin cos + 2 2 2 2 . 2 1 arcsin 2 2 2 2 x a x C a a x = + − + t a x 2 2 a − x 例17 求 d ( 0). 2 2 −   a x x a t a x 2 2 a − x 第二节 换元积分法 解 例18 求 令 x = atan t , , 2 π 2 π −  t  则 2 2 x + a a a t 2 2 2 = + tan = asect , d sec d , 2 x = a t t  + 2 2 d x a x t a t a t d sec sec2  = sect dt  = = ln |sect + tan t | +C C a x a a x +         + = + 2 2 ln t a x 2 2 x + a ( 0). d 2 2  +  a x a x ( ) 1 2 2 = ln x + x + a +C ( ln ). C1 = C − a 例18 求 ( 0). d 2 2  +  a x a x t a x 2 2 x + a

第二节换元积分法 dx 例19求 (a>0). x2-a 解之 例20求+后 dx 解 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 第二节 换元积分法 解 例19求 当 x > a 时，令 x = asec t , , 2 π 0  t  则 2 2 x − a 2 2 2 = a sec t − a = a tant , dx = asect tant dt,  − 2 2 d x a x t a t a t t d tan sec tan  = sect dt  = = ln |sect + tant | +C C a x a a x +         − = + 2 2 ln t a x 2 2 x − a ( ) 1 2 2 = ln x + x − a +C ( ln ) . C1 = C − a ( 0). d 2 2  −  a x a 例 x 19 求 ( 0). d 2 2  −  a x a x t a x 2 2 x − a 第二节 换元积分法 解 例20 求 . d  2 2 2 x x + a x 令 , 1 t x = 则   +            − = 2 2 2 2 1 1 d 1 a t t t t  + 2 2 2 d x x a x  + = − 2 2 1 d a t t t  + + = − 2 2 2 2 2 1 d(1 ) 2 1 a t a t a a t C a = − + + 2 2 2 1 1 C a x x a + + = − 2 2 2 例20 求 . d  2 2 2 x x + a x

第二节换元积分法 第二换元积分法常用的4种代换 ()x=asin t用于被积函数中含有√a2-x2, (2)x=atant用于被积函数中含有√x2+a2 (3)x=asect用于被积函数中含有√x2-a2, 1 (4) X=- 用于将被积函数分母中的高次因子翻 到分子上去，使分母的次数降低， 上页 下页 返回 MathGS 公式 线与面 数学家

第二节 换元积分法 第二换元积分法常用的4种代换 (1) x = asin t 用于被积函数中含有 , 2 2 a − x (2) x = atan t 用于被积函数中含有 , 2 2 x + a (3) x = asec t 用于被积函数中含有 , 2 2 x − a (4) 用于将被积函数分母中的高次因子翻 t x 1 = 到分子上去，使分母的次数降低