《高等数学》课程教学资源（PPT课件）第三章微分中值定理与导数的应用_第五节函数的极值与最大值最小值

第五节函数的极值与最大值最小值 一、函数的极值及其求法 二、最大值最小值问题 上页 下页 返回 MathS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 一、函数的极值及其求法 二、最大值最小值问题

第五节函数的极值与最大值最小值 函数的极值及其求法 1.函数极值的定义 定义设函数f心)在点xo的某邻域U)内有定义， 如果对该邻域内的任一x(心≠x),有 fx)f)), 那么就称f)是函数f)的一个极大值（或极小值） 函数的极大值与极小值统称为极值，使函数取得极 值的点称为极值点。 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 1. 函数极值的定义 一、函数的极值及其求法 定义 设函数 f (x) 在点 x0 的某邻域 U(x0 ) 内有定义, 如果对该邻域内的任一 x (x  x0 )，有 f (x) f (x0 ) )， 那么就称 f (x0 ) 是函数 f (x) 的一个极大值(或极小值). 函数的极大值与极小值统称为极值，使函数取得极 值的点称为极值点

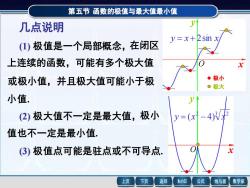
第五节函数的极值与最大值最小值 几点说明 y=x+2sin x ()极值是一个局部概念，在闭区 上连续的函数，可能有多个极大值 或极小值，并且极大值可能小于极 。极小 。极大 小值. (2)极大值不一定是最大值，极小 y=(x-4/ 值也不一定是最小值. (③)极值点可能是驻点或不可导点： x 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 几点说明 (1) 极值是一个局部概念，在闭区 上连续的函数，可能有多个极大值 或极小值，并且极大值可能小于极 小值. (2) 极大值不一定是最大值，极小 值也不一定是最小值. (3) 极值点可能是驻点或不可导点. y = x + 2sin x x y 极小 极大 O 2 3 2 y = (x − 4) x x y O

第五节函数的极值与最大值最小值 2.极值存在的条件 定理1（必要条件）设函数fw)在处可导，且在 xo处取得极值，那么f'c)=0. 定理1说明：可导函数的极值点一定是驻点，但驻点 不一定是极值点.例如函数 y(x-)3+2 y=(x-1)3+2在驻点x=1处不 取得极值，因为该函数在其定义 域内是单调增函数. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 2. 极值存在的条件 定理1(必要条件) 设函数 f (x) 在 x0 处可导，且在 x0 处取得极值，那么 f (x0 ) = 0 . 定理1说明：可导函数的极值点一定是驻点，但驻点 不一定是极值点. ( 1) 2 3 y = x − + 例如函数 在驻点 x = 1 处不 取得极值，因为该函数在其定义 域内是单调增函数. ( 1) 2 3 y = x − + x y O

第五节函数的极值与最大值最小值 定理2（第一充分条件）设函数fx)在连续，且 在的某去心邻域内可导. (1)若x0,而x>xo时，f')时，f'c)>0, 则f)在处取得极小值；（左负右正）八/ 3)若在的左右两侧f'心)不变号，则fx)在x0 处不取得极值.一 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 定理2(第一充分条件) 设函数 f (x) 在 x0 连续，且 在 x0 的某去心邻域内可导. (1) 若 x 0，而 x > x0 时， f (x) x0 时， f (x) > 0， 则 f (x) 在 x0 处取得极小值；(左负右正) (3) 若在 x0 的左右两侧 f (x) 不变号，则 f (x) 在 x0 处不取得极值

第五节函数的极值与最大值最小值 定理3（第二充分条件）设函数fx)在x处具有二 阶导数且f'心o)=0,f"c)≠0，那么 (1)当f"co)0时，函数fx)在o处取得极小值. 证明 定理3表明，当二阶导数在驻点处不为零时，可以用 二阶导数的符号来判定函数在该驻点处是取得极大值 还是极小值 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 定理3(第二充分条件) 设函数 f (x) 在 x0 处具有二 阶导数且 f (x0 ) = 0， f  (x0 )  0， (1) 当 f (x0 ) 0 时,函数 f (x) 在 x0 处取得极小值. 第五节 函数的极值与最大值最小值 证明 f (x0 ) = 0， f  (x0 )  0， (1) 当 f (x0 ) 0 时,函数 f (x) 在 x0 处取得极小值. (1) f (x0 ) < 0 0 0 0 ( ) ( ) ( ) lim 0 x x f x f x f x x x −  −   = → , ( ) 0 lim 0 x x f x x x −  = → 当函数极限的局部保号性，存在 x0 的某一去心邻域， 在该邻域内有 0 . ( ) 0  −  x x f x 定理3表明，当二阶导数在驻点处不为零时， 二阶导数的符号来判定函数在该驻点处是取得极大值 还是极小值. 可以用

第五节函数的极值与最大值最小值 3.求极值的步骤 Step1求导数f'x); Step2求出函数的全部驻点与不可导点； Step3用第一充分条件或第二充分条件判别在Step2 中求出的这些点处函数是否取得极值，并进一步确定 是极大值还是极小值； Step4求出各极值点的函数值，就得函数的全部极 值. 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 3. 求极值的步骤 Step1 求导数 f (x)； Step2 求出函数的全部驻点与不可导点； Step3 用第一充分条件或第二充分条件判别在Step2 中求出的这些点处函数是否取得极值， 并进一步确定 是极大值还是极小值； Step4 求出各极值点的函数值，就得函数的全部极 值

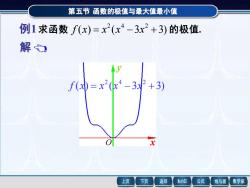
第五节函数的极值与最大值最小值 例1求函数f(x)=x2(x4-3x2+3)的极值. 解 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 第五节 函数的极值与最大值最小值 函数的极值与最大值最小值 解 例1 求函数 ( ) ( 3 3) 2 4 2 f x = x x − x + 的极值. ( ) 6 ( 1) , 2 2 f  x = x x − ( ) 6( 1)(5 1) . 2 2 f  x = x − x − 令 f (x) = 0 解得驻点为 x1 = -1 , x2 = 0 , x3 = 1 . 因为 f (0) = 6 > 0，所以在驻点 x2 = 0 处取得极小值 f (0) = 0 . 由于 f (-1) = f (1) = 0，所以在驻点 x1 , x3 处 不能应用第二充分条件. 但是当 x 取 x1 左右两侧附近 的值时，f (x) 0，所以由第一充分条件知,这两点均不是极值点. 例1 求函数 ( ) ( 3 3) 2 4 2 f x = x x − x + 的极值. O x y ( ) ( 3 3) 2 4 2 f x = x x − x +

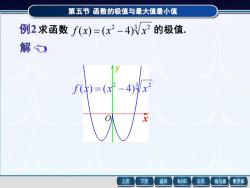
第五节函数的极值与最大值最小值 例2求函数f(x)=(x2-4)/x2的极值. 解 f()=(x -4)x 上页 下页 返回 MathS 公式 线与面 数学家

第五节 第五节 函数的极值与最大值最小值 函数的极值与最大值最小值 解 例2 求函数 2 3 2 f (x) = (x − 4) x 的极值. . ( 1)( 1) 3 8 ( ) 3 x x x f x − +  =  由此可得驻点为 -1 , 1 . 另外，当 x = 0 时，f (x)不存在. 用第一充分条件判别，列表如下： f (x) f (x) (-,-1) -1 (-1, 0) 0 (0, 1) – 0 1 (1,+) + 不  – 0 + -3 0 -3 极 小 值 极 大 值 极 小 值 例2 求函数 2 3 2 f (x) = (x − 4) x 的极值. x y O 2 3 2 f (x) = (x − 4) x

第五节函数的极值与最大值最小值 二、最大值最小值问题 我们知道在闭区间[，b]上连续的函数，一定取得 得最大值和最小值.下面来求最大值和最小值。 假设函数fx)在闭区间[a,b]上连续，在(a,b)内 除有限个点外可导，且至多有有限个驻点.则求其最大 值和最小值的步骤如下： 上页 下页 返回 MathGS 公式 线与面 数学家

第五节 函数的极值与最大值最小值 二、最大值最小值问题 我们知道在闭区间 [a , b] 上连续的函数，一定取得 得最大值和最小值. 下面来求最大值和最小值. 假设函数 f (x) 在闭区间[a , b] 上连续，在 (a , b) 内 除有限个点外可导，且至多有有限个驻点. 则求其最大 值和最小值的步骤如下：