《高等数学》课程教学资源（PPT课件）第一章函数与极限_第八节函数的连续性与间断点

第八节函数的连续性与间断点 一、 函数的连续性 二、函数的间断点 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 一、函数的连续性 二、函数的间断点

第八节函数的连续性与间断点 一、函数的连续性 1.变量的增量 定义设变量u从初值W1变到终值2， 终值与初值 的差w2-w1称为变量u的增量，记作 △u=u2-l1· 设y=f(x),则△x称为自变量的增量，△y称为函 数的增量. 注意增量△可正可负还可以为零， 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 一、函数的连续性 1. 变量的增量 定义 设变量 u 从初值 u1 变到终值 u2 ，终值与初值 的差 u2 – u1 称为变量 u 的增量，记作 u = u2 – u1 . 设 y = f (x)，则 x 称为自变量的增量， y称为函 数的增量. 注意 增量 u 可正可负还可以为零

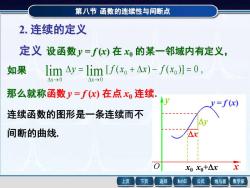
第八节函数的连续性与间断点 2.连续的定义 定义设函数y=fx)在的某一邻域内有定义， 如果 lim△y=lim[f(x+△x)-f(xo】=0, △x→0 Ax-0 那么就称函数y=fx)在点x连续， =f(x) 连续函数的图形是一条连续而不 间断的曲线 xoxo+△x 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 x y O x0 x0+x x y y = f (x) 2. 连续的定义 定义 设函数 y = f (x) 在 x0 的某一邻域内有定义， 如果 [ ( ) ( ) ] 0 , 0 0 0 0 lim  = lim +  − =  →  → y f x x f x x x 那么就称函数 y = f (x) 在点 x0 连续. 连续函数的图形是一条连续而不 间断的曲线

第八节函数的连续性与间断点 lim△y=lim[f(x+△x)-f(x】=0, △x→0 △x→0 3.连续的等价定义 令x=x,+△x,则可得连续的如下等价定义： 定义设函数y=fc)在x的某一邻域内有定义， 如果 lim f(x)=f(x), x→x0 那么就称函数y=f心)在点x连续 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 3. 连续的等价定义 令 x = x0 + x , [ ( ) ( ) ] 0 , 0 0 0 0 lim  = lim +  − =  →  → y f x x f x x x 则可得连续的如下等价定义： 定义 设函数 y = f (x) 在 x0 的某一邻域内有定义， 如果 ( ) ( ) , lim 0 0 f x f x x x = → 那么就称函数 y = f (x) 在点 x0 连续

第八节函数的连续性与间断点 ()有定义，即fx)存在； limf(x)=f(x)(2)有极限，即limf(x)存在； x→x0 (3)相等，即limf(x)=f(x) x→x0 因此函数y=f(x)在点x连续必需同时满足上述三 个条件 上页 下页 返回 MathS 公式 线与面 数学家

第八节 函数的连续性与间断点 ( ) ( ) lim 0 0 f x f x x x = → (1) 有定义，即 f (x0 ) 存在； (2) 有极限，即 ( ) lim 0 f x x→x 存在； (3) 相等，即 ( ) ( ) . lim 0 0 f x f x x x = → 因此函数 y = f (x) 在点 x0 连续必需同时满足上述三 个条件

第八节函数的连续性与间断点 4.连续函数 左连续：limf(x)=f(x,)=f(xo). 右连续：1imf(x)=f(x,)=f(x). x→x0 连续：f(x,)=f(x)=f(x,) 定义在区间上每一点都连续的函数，叫做在该区间 上的连续函数，或者称函数在该区间上连续.如果区间 包括端点，那么在左端点连续是指右连续，在右端点 连续是指左连续 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 4. 连续函数 左连续： ( ) ( ) ( ) . lim 0 0 0 f x f x f x x x = = − → − 右连续： ( ) ( ) ( ) . lim 0 0 0 f x f x f x x x = = + → + 连 续： ( ) ( ) ( ) . 0 0 0 − + f x = f x = f x 定义 在区间上每一点都连续的函数，叫做在该区间 上的连续函数，或者称函数在该区间上连续. 如果区间 包括端点，那么在左端点连续是指右连续，在右端点 连续是指左连续

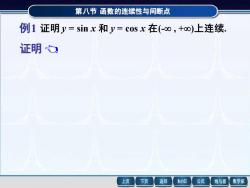
第八节函数的连续性与间断点 例1证明y=sinx和y=c0sx在(-o0,+oo)上连续 证明 上页 下页 返回 MathS 公式 线与面 数学家

第八节 函数的连续性与间断点 例1 证明 y = sin x 和 y = cos x 在(- , +)上连续. 第八节 函数的连续性与间断点 证明 例1 证明 y = sin x 和 y = cos x 在(- , +)上连续.  x  (- , +)， y = sin( x + x) −sin x 因为 所以        +  = 2 cos 2 2sin x x x 0  | y | 2 2sin x   | x | . 而 | | 0 , lim 0  =  → x x 因此由夹逼定理有 0 . lim 0  =  → y x 这就证明了 y = sin x 在(- , +)上连续. , 2 cos 2 2sin        +  = x x x 同理可证 y = cos x 在(- , +)上连续

第八节函数的连续性与间断点 二、函数的间断点 定义设函数y=fx)在x的某一邻域内有定义， 如果函数y=fx)有下列三种情形之一： (1)在x=x没有定义； 2)虽在x=xo有定义，但limf(x)不存在； (3)虽在x=x有定义，且limf(x)存在，但 x→X0 limf(x)≠f(x), X->X0 则称函数fx)在x间断，点x称为函数fx)的间断点 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 二、函数的间断点 定义 设函数 y = f (x) 在 x0 的某一邻域内有定义， 如果函数 y = f (x) 有下列三种情形之一： (1) 在 x = x0 没有定义； (2) 虽在 x = x0 有定义，但 ( ) lim 0 f x x→x 不存在； (3) 虽在 x = x0 有定义，且 ( ) lim 0 f x x→x 存在，但 ( ) ( ) , lim 0 0 f x f x x x  → 则称函数 f (x)在 x0 间断，点x0 称为函数f (x)的间断点

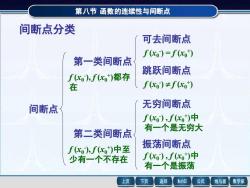
第八节函数的连续性与间断点 间断点分类 可去间断点 f(xo)=f(xo) 第一类间断点 跳跃间断点 c0),f)都存 在 f(x)≠f(c,) 间断点 无穷间断点 fc0),f)中 第二类间断点 有一个是无穷大 f),fc)中至 振荡间断点 少有一个不存在 f0),f)中 有一个是振荡 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 间断点分类 间断点 第一类间断点 f (x0 - ), f (x0 + )都存 在 可去间断点 f (x0 - ) = f (x0 + ) 跳跃间断点 f (x0 - )  f (x0 + ) 第二类间断点 f (x0 - ), f (x0 + )中至 少有一个不存在 无穷间断点 f (x0 - ) , f (x0 + )中 有一个是无穷大 振荡间断点 f (x0 - ) , f (x0 + )中 有一个是振荡

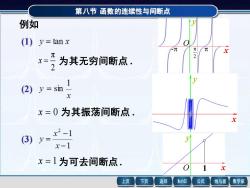
第八节函数的连续性与间断点 例如 (1)y=tanx x=为其无穷间断点 (2) y=sin x=0为其振荡间断点. (3) J= x2-1 x-1 x=1为可去间断点， 上页 下页 返回 MathGS 公式 线与面 数学家

第八节 函数的连续性与间断点 π 2 x = 为其无穷间断点 . x = 0 为其振荡间断点 . x = 1 为可去间断点 . 例如 x y (1) (2) (3) x y O 1 x y O 2 - π 