《高等数学》课程教学资源（PPT课件）第五章 定积分_5-3 换元分部积分

第三节 第五章 定积分的换无法和 分部积分法 不定积分 换元积分法 换元积分法 定积分 分部积分法 分部积分法 定积分的换元法 二、定积分的分部积分法 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、定积分的分部积分法 第三节 不定积分 机动 目录 上页 下页 返回 结束 一、定积分的换元法 换元积分法 分部积分法 定积分 换元积分法 分部积分法 定积分的换元法和 分部积分法 第五章

一、定积分的换元法 定理1.设函数f(x)∈Ca,b],单值函数x=p(t)满足 1)p(t)eC'[a,β]，p(a)=a,p(β)=b, 2)在[C,]上a≤p(t)≤b, 则 d-fIdr 证：所证等式两边被积函数都连续，因此积分都存在 且它们的原函数也存在.设F(x)是f(x)的一个原函数， 则F[p(t)]是f[o(t)]p'()的原函数，因此有 [f(x)dx=F(b)-F(a)=FIp(B)]-FIp(a)] ["Slo()]p(t)dt HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、定积分的换元法 定理1. 设函数 单值函数 满足: 1) ( ) [ , ], 1  t C   2) 在 [ , ] 上 () = a,() = b; (t) (t) 证: 所证等式两边被积函数都连续, 因此积分都存在 , 且它们的原函数也存在 . 则 是 的原函数 , 因此有 = F(b) − F(a) = F[()] − F[()] (t) (t) (t) (t) (t) 机动 目录 上页 下页 返回 结束 则

心fxdr=fIo0)o'e)dr 说明： 1)当B<α，即区间换为[B,c]时，定理1仍成立 2)必需注意换元必换限，原函数中的变量不必代回 3)换元公式也可反过来使用，即 ()d=f()dx() 或配元∫/Lp(u)p')di=∫f[p)]dp(t) 配元不换限 HIGH EDUCATION PRESS 机动目录上页下页返回结束

说明: 1) 当 <  , 即区间换为 [ ,]时， 定理 1 仍成立 . 2) 必需注意换元必换限 , 原函数中的变量不必代回 . 3) 换元公式也可反过来使用 , 即 f x x (令x =(t)) b a ( )d  = 或配元 (t) d(t) 配元不换限 (t) (t) 机动 目录 上页 下页 返回 结束 (t) (t) (t) (t)

例1.计算 i ["a2-x2dx (a>0). 解：令x=asint,则dx=acostdt,且 当x=0时，1=0；x=a时，t= 原式=a2cos2tdt yy=va2-x2 -g月0+eos2n)d, a2 2(+2sn2) πa HIGH EDUCATION PRESS eOC①8 机动目录上页下页返回结束

例1. 计算 解: 令 x = asint, 则 dx = acost dt , 当x = 0时, t = 0; , . 2  x = a 时 t = ∴ 原式 = 2 a t t a (1 cos 2 )d 2 2 0 2  = +  sin 2 ) 2 1 ( 2 2 t t a = + 0 2   2 0  cos t dt 2 2 2 y = a − x o x y a 机动 目录 上页 下页 返回 结束 且

例2计算∫cossinx. 解令t=cosx, dt=-sinxdx, x=2→t=0,x=0→1=1， Ewra咖a-ra-6g cos*xsin cos'xdcosx 6 6 HIGH EDUCATION PRESS

例2 计算 cos sin . 2 0 5   x xdx 解 令 t = cos x, 2  x =  t = 0, x = 0 t = 1,   2 0 5 cos x sin xdx  = − 0 1 5 t dt 1 0 6 6 t = . 6 1 = dt = −sin xdx,   2 0 5 cos x sin xdx 6 2 0 cos 6 x  = . 6 1 = 2 5 0 cos cos xd x  = 

例3计算 sin'x-sin xdx. a解'"f(x)=Vsin3x-sim=cosx(sinx)月 sinx-sin"xd=cosx(sinx)de eos (sin )cos(sin )e =j后(6 sin x)dsin-」(sindsinx -g6n时e如- HIGH EDUCATION PRESS

例3 计算 解 sin sin . 0 3 5   x − xdx f x x x 3 5  ( ) = sin − sin ( )2 3 = cos x sin x    − 0 3 5 sin x sin xdx ( )   = 0 2 3 cos x sin x dx ( )   = 2 0 2 3 cos x sin x dx ( )   −  2 2 3 cos x sin x dx ( )   = 2 0 2 3 sin x d sin x ( )   −  2 2 3 sin x d sin x ( ) 2 0 2 5 sin 5 2  = x ( )   − 2 2 5 sin 5 2 x . 5 4 =

例4.计算 dx 解令1=2x+1,则x-21dk=1d,且 2 当x=0时，t=1;x=4时，1=3. =e-3)a -3的39号 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例4. 计算 解: 令 t = 2x +1, 则 , d d , 2 1 2 x t t t x = − = 当x = 0时, x = 4时, t = 3. ∴ 原式 = t t t t d 3 2 1 2 1 2  + − (t 3)dt 2 1 3 1 2  = + 3 ) 3 1 ( 2 1 3 = t + t 1 3 t =1; 机动 目录 上页 下页 返回 结束 且

例5.设f(x)eCL-a,a, 偶倍奇零 (1)若f(-x)=fx),则fx)dx=20f(x)d 2)若f(-x)=-f(x),则，f(x)dx=0 证，fw)d=fx山+9f6d =J0f(-)dr+∫fx)d 令x=- =If(-x)+f(x)]dx 。7 f(-x)=-f(x)时 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例5. 证: (1) 若   − = a a a f x x f x x 0 则 ( )d 2 ( )d = − f x x a a ( )d (2) 若 ( )d = 0 − a a 则 f x x f x x a ( )d 0 − f x x a ( )d 0  + f t t a ( )d 0  = − f x x a ( )d 0  + f x f x x a [ ( ) ( )]d 0  = − + f (−x) = f (x)时 f (−x) = − f (x)时 偶倍奇零 机动 目录 上页 下页 返回 结束 令x = −t =

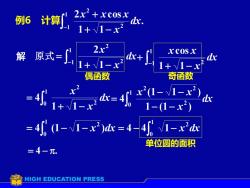
例6 计算 2x2+xcosx dx. 1+1-x2 解原式= 2x2 d&+ xCOsx 1+1-x 1+1-xi 偶函数 奇函数 或e =4(1-V1-x2)=4-41-x 单位圆的面积 =4-元. HIGH EDUCATION PRESS

奇函数 例6 计算 解 . 1 1 1 2 cos 1 2 2 − + − + dx x x x x 原式 − + − = 1 1 2 2 1 1 2 dx x x − + − + 1 1 2 1 1 cos dx x x x 偶函数  + − = 1 0 2 2 1 1 4 dx x x  − − − − = 1 0 2 2 2 1 (1 ) (1 1 ) 4 dx x x x  = − − 1 0 2 4 (1 1 x )dx  = − − 1 0 2 4 4 1 x dx = 4 − . 单位圆的面积

例7.若f(x)eCI0,1],试证： 店/6 sin=月f(cos.x)bx.⑥ 证 (sinx)ds1.chd π 2x=21=01 -f(cost)ii=f(cosx)d HIGH EDUCATION PRESS

( ) ( )   = 20 20 sin cos   f x dx f x dx . ⑤  f t dt sin      − −          02 2 证 ( ) ( )   = = 20 20 cos cos   f t dt f x dx 例 7. 若 试证 : , , ; , x t dx dt x t x t    = − = − = = = = 2 0 0 2 2 f x dx (sin )   20