《高等数学》课程教学资源（PPT课件）第二章 导数与微分_2-1 导数概念

第之章 导数思想最早由法国 数学家Ferma在研究 导数与微分 极值问题中提出. 微积分学的创始人： 英国数学家Newton 德国数学家Leibniz 导数 描述函数变化快慢 微分学 微分 描述函数变化程度 都是描述物质运动的工具（从微观上研究函数）

第二章 微积分学的创始人: 德国数学家 Leibniz 微分学 导数 描述函数变化快慢 微分 描述函数变化程度 都是描述物质运动的工具 (从微观上研究函数) 导数与微分 导数思想最早由法国 数学家 Ferma 在研究 极值问题中提出. 英国数学家 Newton

第一节 第二章 导教的橇念 、 引例 二、 导数的定义 三、 导数的几何意义 四、 函数的可导性与连续性的关系 五、单侧导数 HIGH EDUCATION PRESS 凯动 录上页下页返回结束

一、引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、单侧导数 第一节 机动 目录 上页 下页 返回 结束 导数的概念 第二章

一、引例 1.变速直线运动的速度 设描述质点运动位置的函数为 s=f(t) 则t,到t的平均速度为 =1-f(to) f(t】 t-to to 而在t,时该刻的瞬时速度为 y lim f(t)-f(0) 1→to t-to HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、 引例 1. 变速直线运动的速度 设描述质点运动位置的函数为 0 t 则 到 的平均速度为 v = ( ) ( ) 0 f t − f t 0 t − t 而在 时刻的瞬时速度为 lim 0 t t v → = ( ) ( ) 0 f t − f t 0 t − t s o ( )0 f t f (t) t 机动 目录 上页 下页 返回 结束

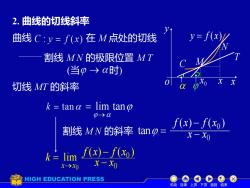
2.曲线的切线斜率 曲线C:y=f(x)在M点处的切线 y=f(x)/ 割线MN的极限位置MT (当p→时) 切线MT的斜率 k tana lim tan 0→C 割线MN的斜率tanp= f(x)-f(xo)】 x-X0 k÷lim)-fx) x->x0 x-X0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

x y o y = f (x) C 2. 曲线的切线斜率 曲线   N T 0 x M 在 M 点处的切线 x 割线 M N 的极限位置 M T (当 时) 割线 M N 的斜率 tan = ( ) ( ) 0 f x − f x 0 x − x 切线 MT 的斜率    lim tan → = lim 0 x x k → = ( ) ( ) 0 f x − f x 0 x − x 机动 目录 上页 下页 返回 结束

瞬时速度v=1im f()-f(o) t-→to t-to 切线斜率k=lim f(x)-(x) x→X0 x-x0 两个问题的共性： 所求量为函数增量与自变量增量之比的极限 类似问题还有： 加速度是速度增量与时间增量之比的极限 角速度是转角增量与时间增量之比的极限 线密度是质量增量与长度增量之比的极限 变化率问题 电流强度是电量增量与时间增量之比的极限 HIGH EDUCATION PRESS 机动目录上页下页返回结束

两个问题的共性: s o 0 t ( )0 f t f (t) 瞬时速度 t 切线斜率 x y o y = f (x) C   N T 0 x M x 所求量为函数增量与自变量增量之比的极限 . 类似问题还有: 加速度 角速度 线密度 电流强度 是速度增量与时间增量之比的极限 是转角增量与时间增量之比的极限 是质量增量与长度增量之比的极限 是电量增量与时间增量之比的极限 变 化 率 问 题 机动 目录 上页 下页 返回 结束 

二、导数的定义 定义1.设函数y=f(x)在点x,的某邻域内有定义 若 1imf)-fo）=1imAy △y=f(x)-f(x》 X→x0 x-X0 △x→0△X △X=X-X0 存在，则称函数f(x)在点x处可导， 并称此极限为 y=∫(x)在点x。的导数记作 w器- df(x) dx =xo 即 x=f(xo)lim,Ay Ax→0△X lim f(x,+△x)-(xo) lim f(xo+h)-f(xo) △x→0 △x -→0 HIGH EDUCATION PRESS 凯动目录上页下页返回结束

二、导数的定义 定义1 . 设函数 在点 0 lim x→x 0 0 ( ) ( ) x x f x f x − − x y x   =  →0 lim ( ) ( )0 y = f x − f x 0  x = x − x 存在, 并称此极限为 记作: ; 0 x x y =  ( ) ; 0 f  x ; d d 0 x x x y = d 0 d ( ) x x x f x = 即 0 x x y =  ( ) 0 = f  x x y x   =  →0 lim 则称函数 若 的某邻域内有定义 , 在点 处可导, 在点 的导数. 机动 目录 上页 下页 返回 结束

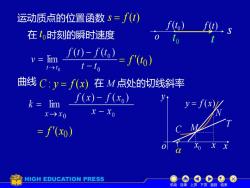
运动质点的位置函数S=f(t) f(,) 在t时刻的瞬时速度 v lim f()-f()」 1→10 t-to 曲线C:y=f(x)在M点处的切线斜率 =lim f(x)-f(x)】 y x→x0 x-Xo f(xo) HIGH EDUCATION PRESS ◆0C08 机动目录上页下页返回结束

运动质点的位置函数 s = f (t) s o 0 t ( )0 f t f (t) 在 时刻的瞬时速度 t 0 t 曲线 C : y = f (x) 在 M 点处的切线斜率 x y o y = f (x) C  N T 0 x M x ( ) 0 = f  t ( ) 0 = f  x 机动 目录 上页 下页 返回 结束

lim f(x)-∫() lim △y △y=f(x)-f(x) x→x0 x-xo △x→0△X △X=X-X0 若上述极限不存在，就说函数在点x不可导 若1imy=0,也称/()在xo的导数为无穷大 △x>0△X 若函数在开区间1内每点都可导，就称函数在1内可导 此时导数值构成的新函数称为导函数 记作y:): .df(x) d ’dx 注意)==≠ dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

( ) ( )0 y = f x − f x 0  x = x − x 若上述极限不存在 , 在点 不可导. 0 x 若 lim , 0 =     → x y x 也称 在 若函数在开区间 I 内每点都可导, 此时导数值构成的新函数称为导函数. 记作: y ; f (x) ; ; d d x y . d d ( ) x f x 注意: ( )0 f  x 0 ( ) x x f x = =  x f x d d ( ) 0  就说函数 就称函数在 I 内可导. 的导数为无穷大 . 机动 目录 上页 下页 返回 结束

例1.求函数f(x)=C(C为常数)的导数 解：y=imfx+Aw)-f1im C-C =0 △x→0 △x △x→0△X 即 (C)y'=0 例2.求函数f(x)=x”(n∈N)在x=a处的导数， 解：f'o)=lmf)-f@=1im-a x-→a x-a x→ax-a =lim(x"-+ax"-2+a2x"-3+.+a-l） x→a =nan-l HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 求函数 (C 为常数) 的导数. 解: y  即 例2. 求函数 解: x a f x f a − ( ) − ( ) x→a = lim x a x a n n x a − − = → lim lim( x→a = n−1 x −2 + n a x 2 −3 + n a x + ) −1 + n a x f x x f x  ( +  ) − ( ) 0 lim  → = x 机动 目录 上页 下页 返回 结束

说明： 对一般幂函数y=x“(4为常数) (x“)y=ux (以后将证明) 脚，5y=y=-2 ()=y=-H- HIGH EDUCATION PRESS 机动目录上页下页返回结束

说明： 对一般幂函数  y = x (  为常数) 1 ( ) −  =   x  x 例如， ( x ) ( ) 2 1 = x  2 1 2 1 − = x 2 x 1 = ( )  x 1 ( ) 1 =  − x −1−1 = −x 2 1 x − = ) 1 (  x x ( ) 4 3 =  − x 4 7 4 −3 − = x （以后将证明） 机动 目录 上页 下页 返回 结束