《高等数学》课程教学资源（PPT课件）第一章 函数与极限_1-6 极限存在准则

第之为 第一章 极限存在准则及 两个重要极限 极限存在准则 夹逼准则单调有界准则 二、两个重要极限 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、 两个重要极限 一、极限存在准则 夹逼准则 单调有界准则 第六节 机动 目录 上页 下页 返回 结束 极限存在准则及 两个重要极限 第一章

1、数列的夹逼准则C准则1)P46 (0)yn≤xm≤2n（n=1,2,.) =>lim xn a (2)lim yn lim zn a n→o0 n→oo 证：由条件(2)，V8>0,3N1,N2, 当n>N1时，yn-aN2时，2m-aN时，有 a-8<ym<a+8,a-8<2n<a+8, 由条件(1) a-E≤yn≤Xn≤2n<a+8 即xn-a<6,故lim=a. n-→∞ HIGH EDUCATION PRESS 机动目录上页下页返回结束

y z a n n n n = = → → (2) lim lim 1、数列的夹逼准则(准则1)(P46) (1) y  x  z ( n = 1, 2, ) n n n x a n n = → lim 证:由条件 (2) ,   0, , N1 当 时, 当 时, 令 max , , N = N1 N2 则当 n  N 时, 有 由条件 (1) n n n a −   y  x  z  a +  即 x − a   , n 故 lim x a . n n = → , N2 机动 目录 上页 下页 返回 结束

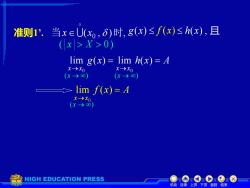
准则1.当x∈U(x,δ)时，8(x)≤f(x)≤h(x),且 (x>X>0) lim g(x)=lim h(x)=4 x→x0 X→x0 (x-→0)】 (x→∞) lim f(x)=A x→x0 (x→>o0 HIGH EDUCATION PRESS eOC①8 机动目录上页下页返回结束

机动 目录 上页 下页 返回 结束 准则1’. g x h x A x x x x = = → → lim ( ) lim ( ) 0 0 g(x)  f (x)  h(x) , f x A x x = → lim ( ) 0 ( x  X  0 ) (x → ) (x → ) (x → ) 当x (x0 ,  )时, 且  

重要极限 1.lim sinx =1 x→0 证：当x∈(0，)时， △AOB的面积0 x>0 HIGH EDUCATION PRESS 注目录上页下页返回结束

1 sin cos   x x x 圆扇形AOB的面积 重要极限 证: 当 即 sin x  2 1 tan x 2 1  亦即 sin tan (0 ) 2  x  x  x  x  (0, ) 2   x 时， (0 ) 2  显然有  x  △AOB 的面积＜ ＜△AOD的面积 D C B A x 1 o 故有 注 注 目录 上页 下页 返回 结束

例2.求1im tan x x→0X 解： lim tan x sinx lim x→0 x-→0 X COS X sinx lim x-→0x f = x-→0C0Sx 例3.求1im arcsin x x→0 X 解：令t=arcsinx,则x=sint,因此 原式=lim,=lim =1 t-→0Slnt t→0 sint HIGH EDUCATION PRESS eOC①8 机动目录上页下页返回结束

例2. 求 解: x x x tan lim →0       = → x x x x cos sin 1 lim 0 x x x sin lim →0 = x cos x 1 lim →0  =1 例3. 求 解: 令 t = arcsin x , 则 x = sin t , 因此 原式 t t t sin lim →0 = t sin t =1 机动 目录 上页 下页 返回 结束

1-cosx 例4.求1im x>0 解：原式=四x2 x→0 2- r-月 说明：计算中注意利用 lim sin(x) (x)>0 (x) HIGH EDUCATION PRESS 机动目录上页下页返回结束

例4. 求 解: 原式 = 2 2 2 0 2sin lim x x x→ 2 1 2 1 =  说明: 计算中注意利用 2 0 sin lim       = x→ 2 x 2 x 2 1 机动 目录 上页 下页 返回 结束

2.单调有界数列必有极限（准则2）(P48) ≤x2≤.≤xn≤xn+l≤.≤M > lim=a(≤M） n→0 为≥x2≥.≥xn≥xn+1≥.≥m >1imxn=b(≥m) n->00 m n+1 x2 X 证明略) HIGH EDUCATION PRESS 0◆0C08 机动目录上页下页返回结束

2. 单调有界数列必有极限 ( 准则2 ) ( P48) lim x a ( M ) n n =  → lim x b ( m ) n n =  → ( 证明略 ) a b 机动 目录 上页 下页 返回 结束

例5.设xn=(1+)”(n=1,2,),证明数列{xn} 极限存在.P49~P50) 证：利用二项式公式，有 xn=(1+) 2n2 31 +nn-l)(n-n+1) n =1+1+2(1-月)+(1-h)(1-分)+. +(1-)(1-分.(1-号) HIGH EDUCATION PRESS 动目录上页下页返回结束

例5. 设 证明数列 极限存在 . (P49～P50) 证: 利用二项式公式 , 有 n n n x (1 ) 1 = + = 1 + n n 1 1! 2 1 2! ( 1) n n n− + 3 1 3! ( 1)( 2) n n n− n− + + n n n n n n n 1 ! ( −1) ( − +1) +  = 1+1+ (1 ) 1 ! 1 n n + − (1 ) 2 n − (1 ) 1 n n−  − (1 ) 1 2! 1 n − (1 1 ) + 3! 1 n + − (1 ) 2 n − 机动 目录 上页 下页 返回 结束

xm=1+1+(1-2)+(1-》)(1-分)+ +(1-7)(1-.(1-m》 x=1+1+2-)+1-0-) 大 大 t0-1-n4)(1-4 正 比较可知 xn<xn+1(n=1,2,.） 又n=(0+”<1+1+2+++ HIGH EDUCATION PRESS 机动目录上页下页返回结束

xn =1+1+ (1 ) 1 ! 1 n n + − (1 ) 2 n − (1 ) 1 n n−  − (1 ) 1 2! 1 n − (1 1 ) + 3! 1 n + − (1 ) 2 n − xn+1 =1+1+ (1 ) 1 1 2! 1 + − n (1 )(1 ) 1 2 1 1 3! 1 + + + − − n n + (1 )(1 ) (1 ) 1 1 2 1 1 ( 1)! 1 + + + + + − − − n n n n n  大 大 正 ( 1, 2, ) xn  xn+1 n =  = (1+ ) 1+1+ 1 n n n 又 x 比较可知 机动 目录 上页 下页 返回 结束

又 xn=0+)”oo e为无理数，其值为 e=2.718281828459045. HIGH EDUCATION PRESS ●X 题目录上页下页返回结束

根据准则 2 可知数列  xn 记此极限为 e , e n n n + = → lim(1 ) 1 即 有极限 . 原题 目录 上页 下页 返回 结束 = (1+ ) 1+1+ 1 n n n x  1+1+ 又  3 1 2 1 3 − = − n e 为无理数 , 其值为 e = 2.718281828459045