《线性代数》课程教学课件（PPT讲稿，B）第四章 线性方程组 §4.2 齐次线性方程组

第四章线性方程组 §4.2齐次线性方程组 齐次线性方程组的性质 二 、基础解系及其求法 三、小结

第四章 线性方程组 三、小结 二、基础解系及其求法 一、齐次线性方程组的性质 §4.2 齐次线性方程组

第四章线性方程组 齐次线性方程组解的性质 设有齐次线性方程组 01X1+012X2+.+41nXn=0 21K1+22X2+.+2mXn=0 (4-5) ml1+0m2X2+.+AmnXn=0 若记 11 12 n 七 A= l24 L22 A2n Am Am2 心 n

第四章 线性方程组 设有齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     若记 （4-5） 一、齐次线性方程组解的性质 11 12 1 1 21 22 2 2 1 2 , n n m m mn n a a a x a a a x A x a a a x             = =            

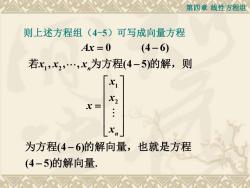
第四章线性方程组 则上述方程组(4-5)可写成向量方程 Ax=0 (4-6) 若x1,x2,.,x,为方程(4-5)的解，则 X X2 x= Xn 为方程(4-6)的解向量，也就是方程 (4-5)的解向量

第四章 线性方程组 则上述方程组（4-5）可写成向量方程 Ax = − 0 (4 6) 1 2 1 2 , , , (4 5) (4 6) (4 5) n n x x x x x x x −       =       − − 若 为方程 的解，则 为方程 的解向量，也就是方程 的解向量

第四章线性方程组 性质4.2.1两个解向量的和仍然是解向量，即 设5,5是方程组(4-5)的解向量，则5+5也 是方程组(4-5)的解向量. 证明」 只需证明5+5满足方程组(4-6)即可 A5=0,A52=0 ∴.A(51+52)=A51+A52=0 故=51+52也是Ax=0的解

第四章 线性方程组 1 2 1 2 , (4 5 4.2. ) (4 5 1 )     − + − 两个解向量的和仍然是解向量，即 设 是方程组 的解向量， 性质 则 也 是方程组 的解向量. 证明  A( 1 +  2 ) = A 1 + A 2 = 0  A 1 = 0, A 2 = 0 故 x 也是Ax 0的解. =  1 +  2 = 只需证明  1 2 + 满足方程组(4 6) − 即可

第四章线性方程组 性质4.2.2一个解向量的倍数仍是解向量，即 设5是方程组(4-5)的解向量，1是任意数， 则25也是方程组(4-5)的解向量。 证明A(25)=九A(5)=20=0. ∴.入5也是方程组(4-5)的解向量 由性质4.2.1、4.2.2知，齐次线性方程组(4-5)的 解向量的线性组合仍是(4-5)的解向量. 设51,52，5m,是方程组(4-5)的解向量，22，.几n-, 是任意数，则入51+2,52+.+入n-,5m-仍是方程组 (4-5)的解向量

第四章 线性方程组 (4 5) (4 5 . .2 ) 4 2     − − 一个解向量的倍数仍是解向量，即 设 是方程组 的解向量， 是任意数， 则 性质 也是方程组 的解向量. 证明 A A (    1 1 ) = = = ( ) 0 0.  − 也是方程组(4 5)的解向量 由性质4.2.1、4.2.2知，齐次线性方程组(4-5)的 解向量的线性组合仍是(4-5)的解向量 . 1 2 1 2 1 1 2 2 , , , (4 5) , , (4 5) n r n r n r n r             − − − −  −  + ++ − 设 是方程组 的解向量， 是任意数，则 仍是方程组 的解向量

第四章线性方程组 二、基础解系及其求法 方程组(4-5)的全部解向量构成个一个向量空间， 称为方程组(4-5)的解空间.它是”的一个子空间， 如果方程组(4-5)有非零解，由性质4.2.1、4.2.2知， 它一定有无穷多非零解要求出(4-5)的所有解，只需 求出解空间的一个基就行了. 下面我们来求解空间的一个基 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A的 前个列向量线性无关，于是A的行最简形为

第四章 线性方程组 二、基础解系及其求法 方程组(4-5)的全部解向量构成个一个向量空间， 称为方程组(4-5)的解空间. 它是R n的一个子空间. 如果方程组(4-5)有非零解，由性质4.2.1、4.2.2知， 它一定有无穷多非零解.要求出(4-5)的所有解，只需 求出解空间的一个基就行了. 下面我们来求解空间的一个基 设线性方程组(4-5)系数矩阵A的秩为r,不妨假设A的 前r个列向量线性无关，于是A的行最简形为

第四章线性方程组 b 0 b I= rrt n 0 0 0 0 0 0 0 与对应的线性方程组为 -b.rbi.Xn (4-7) X,=-b,+1X,+1-.-b,mXm

第四章 线性方程组 1 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 r n rr rn b b b b I + +               =             1 1, 1 1 1, , 1 1 , (4 7) r r n n r r r r r n n x b x b x x b x b x + + + +  = − −−     −  = − −−  与I对应的线性方程组为

第四章线性方程组 显然，线性方程组(4-5)与(4-7)同解，在方程组(4-7中， 给定x+1,Xm一组确定的数，可惟一确定x1,x,的值， 便得到方程组(4-7)的一个解，也就是方程组(4-5)的一 个解，我们把x+1.xn称为自由未知量. 令x+1xn分别取下列n一组数 0 X,+2 .1

第四章 线性方程组 显然，线性方程组(4-5)与(4-7)同解，在方程组(4-7)中， 给定xr+1,.,xn一组确定的数，可惟一确定x1 ,.,xr的值， 便得到方程组(4-7)的一个解，也就是方程组(4-5)的一 个解，我们把xr+1,.,xn称为自由未知量. 令xr+1,.,xn分别取下列n-r组数 1 2 1 0 0 0 1 0 0 0 1 r r n x x x + +                   =                                   ， ，

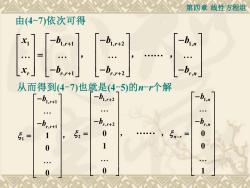
第四章线性方程组 由(4-7)依次可得 01,r+1 x. -b.r -。 从而得到(4-7)也就是(4-5)的-个解 -b1+1 -b1,r+2 一b1,n 一br+1 一br.r+2 51= 5= 0 5n-r= 0 0 1 0 0

第四章 线性方程组 1 1, 1 , 1 r r r r x b x b + +     −        =          −  ， 1, 2 , 2 r r r b b + +   −        −  ， 1, , n r n b b   −        −  ， 由(4-7)依次可得 . 从而得到(4-7)也就是(4-5)的n-r个解 1, 1 , 1 1 1 0 0 r r r b b  + +   −        −   =              ， 1, 2 , 2 2 0 1 0 r r r b b  + +   −        −   =              ， 1, , 0 0 1 n r n n r b b  −   −        −   =              .

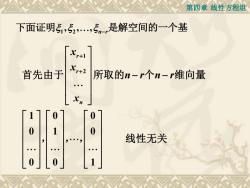
第四章线性方程组 下面证明51,52，5n,是解空间的一个基 首先由于 Xr+2 所取的n-r个n-r维向量 Xn 「0 0 0 1 0 线性无关 0 1

第四章 线性方程组 1 2 , , , n r    下面证明  − 是解空间的一个基 1 2 1 0 0 0 1 0 0 0 1 r r n x x n r n r x + +       − −                                               首先由于 所取的 个 维向量 ， ， ， 线性无关