《线性代数》课程教学课件（PPT讲稿，B）第五章 相似矩阵与二次型 §5.1 向量的内积与正交向量组

第五章相似矩阵与二次型 Ch5 相似矩阵与二次型 ·§5.1向量的内积与正交向量组 ·§5.2方阵的特征值与特征向量 §5.3相似矩阵 ·§5.4实对称矩阵的相似对角形 ·§5.5二次型及其标准型 。§5.6正定二次型

第五章 相似矩阵与二次型 Ch5 相似矩阵与二次型 §5.2 方阵的特征值与特征向量 §5.1 向量的内积与正交向量组 §5.3 相似矩阵 §5.4 实对称矩阵的相似对角形 §5.5 二次型及其标准型 §5.6 正定二次型

第五章相似矩阵与二次型 §5.1向量的内积及正交向量组 内积的定义及性质 二、 向量的长度及性质 三、 正交向量组的概念及求法 四、正交矩阵与正交变换 五、小结思考题

第五章 相似矩阵与二次型 二、向量的长度及性质 五、小结 思考题 三、正交向量组的概念及求法 四、正交矩阵与正交变换 一、内积的定义及性质 §5.1 向量的内积及正交向量组

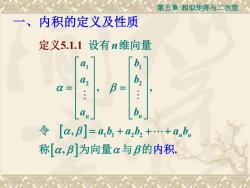
第五章相似矩阵与二次型 一、内积的定义及性质 定义5.1.1 设有n维向量 42 B= b2 0= 令[a,B]=b1+,b2+.+anbn 称[a,B]为向量au与β的内积

第五章 相似矩阵与二次型     1 1 2 2 1 1 2 2 5.1 , , , . , 1 . n n n n n a b a b a b a b a b a b                     = =             = + + + 设有 维向量 令 称 为向量 与 定 的内积 义 一、内积的定义及性质

第五章相似矩阵与二次型 说明： 1. n≥4)维向量的内积是3维向量数量积 的推广，但是没有3维向量直观的几何意义. 2.内积是向量的一种运算，如果a,B都是列 向量，内积可用矩阵记号表示为： [a,β]=ap

第五章 相似矩阵与二次型 说明: 1. n(n≥4)维向量的内积是3维向量数量积 的推广，但是没有3维向量直观的几何意义．   2. , , , : , .       =  内积是向量的一种运算 如果 都是列 向量 内积可用矩阵记号表示为

第五章相似矩阵与二次型 内积的运算性质 (其中a,B,y为n维向量，为实数)： [aB]=[B,a]; (2)[a,B]=[a,B]: (3)[a+B,r]=[a,r]+[B,y]: (4)[a,a]≥0，且当a≠0时有a,a]>0. schwarz不等式[a,B≤[a,alB,B]

第五章 相似矩阵与二次型 内积的运算性质 (其中    , , , : 为n维向量 为实数) (1) , , ;      =   (2) , , ;       =   (3) , , , ;        + = +      (4) [ , ] 0, 0 [ , ] 0.         且当 时有 2 schwarz不等式 [ , ] [ , ][        , ]

第五章相似矩阵与二次型 二、向量的长度及性质 定义5.12非负数√[a,a=√匠++.+称为向量 a的长度（或范数），记作a 向量的长度具有下述性质： 1.非负性当a≠0时，a>0;当x=0时，a=0; 2.齐次性2a=2‖la; 3.三角不等式a+≤a+B:

第五章 相似矩阵与二次型 定义5.1.2   2 2 2 1 2 , . n   a a a   非负数 = + + + 称 长度(或范数 量 的 ) 为向 ，记作 向量的长度具有下述性质： 1. 0 , 0; 0 , 0; 非负性 当      = = 时 当 时 2. ; 齐次性    = 3. . 三角不等式     +  + 二、向量的长度及性质

第五章相似矩阵与二次型 当a=1时，称a为单位向量 如果a≠0，有长度的概念得 a a就是一个单位向量， 用非零数 去乘以向量a得到一个与a同方向的 单位向量，通常称为把向量α单位化， 当a≠0，Bl≠0时，0=arccos [a,B] a 称为n维向量a与B的夹角

第五章 相似矩阵与二次型 当   = 1 , . 时 称 为单位向量 1   0, .  如果  有长度的概念得 就是一个单位向量 1 .     用非零数 去乘以向量 得到一个与 同方向的 单位向量，通常称为把向量 单位化  ,  0, 0 , arccos n .          当   = 时 称为 维向量 与 的夹角

第五章相似矩阵与二次型 三、正交向量组的概念及求法 当a,B]=0时，称向量a与B正交 定义5.1.3一组两两正交的非零向量称为正交向量 组。若正交向量组中每个向量都是单位向量，则称该 向量组为标准正交向量组. 定理5.1.1正交向量组是线性无关向量组. 证明设有，2，.，心m是正交向量组，若有 k a+kaz +.+kam=0 用a,与等式两边做内积，得

第五章 相似矩阵与二次型 定义5.1.3 一组两两正交的非零向量称为正交向量 组．若正交向量组中每个向量都是单位向量,则称该 向量组为标准正交向量组. 三、正交向量组的概念及求法 定理5.1.1 正交向量组是线性无关向量组. 证明 1 1 2 2 0 m m k k k    + + + = , i 用a 与等式两边做内积 得 1 2 , , , 设有   m 是正交向量组，若有 当[ , ] 0     = 时，称向量 与 正交

第五章相似矩阵与二次型 kla,al=0i=1,2,.,m 由a,≠0，有a,]>0,从而得 k=0i=1,2,.,m. 故C1,2,.,nm线性无关， 若a,2,a,是r维向量空间V的一个基，若a1,2, .,两两正交，则称a,2,.,Q是向量空间V的一 个正交基，由单位向量组成的正交基称为标准正交 基（或正交规范基）

第五章 相似矩阵与二次型 0, [ , ] 0, 由   i i i   有 从而得 0 1,2, , . i k i m = = 1 2 , , , . 故   m 线性无关 [ , ] 0 1,2, , i i i k i m   = = 1 2 1 2 1 2 , , , , , , , , , ( ). r r r r V V          若 是 维向量空间 的一个基，若 两两正交，则称 是向量空间 的一 个正交基，由单位向量组成的正交基 标准正交 基 或正交规范基 称为

第五章相似矩阵与二次型 将正交基a1,a2,a,中每个a,单位化后得到 的个单位向量 则e,e2,.,e即为V的一个标准正交基 2 0 例如：4= 为R的一组正交基.将它们单位化得

第五章 相似矩阵与二次型 1 2 1 1 2 2 1 2 1 2 , , , 1 1 1 , , . r i r r r r r e e e e e e V           = = = 将正交基 中每个 单位化后得到 的 个单位向量 ， ， ， 则 ， 即为 的一个标准正交基 1 2 3 3 2 0 1 0 , 1 , 0 1 0 2 R .          −       = = =                   例如： 为 的一组正交基 将它们单位化得