《高等数学》课程教学资源（PPT课件）第一章 函数与极限_1-2 数列的极限

第一章 第二节 教列的教很 一、 数列极限的定义 二、收敛数列的性质 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第一章 二 、收敛数列的性质 一、数列极限的定义 第二节 机动 目录 上页 下页 返回 结束 数列的极限

一、数列极限的定义 引例.设有半径为r的圆，用其内接正边形的面积 A,逼近圆面积S. 如图所示，A,为内接正三边形面积， A,为内接正六边形面积，等等 当n无限增大时，An无限逼近S刘徽割圆术)， 数学语言描述：V&>0,3正整数N,当n>N时，总有 |4n-SKε HIGH EDUCATION PRESS 0◆0C08 刘徽目录上页下页返回结束

数学语言描述: 一 、数列极限的定义 引例. 设有半径为 r 的圆 , 逼近圆面积 S . 如图所示 , 当 n 无限增大时, 无限逼近 S (刘徽割圆术) ,    0 , 正整数 N , 当 n > N 时, A − S   n 用其内接正 n 边形的面积 总有 刘徽 目录 上页 下页 返回 结束 为内接正三边形面积， 为内接正六边形面积，等等

定义：自变量取正整数的函数称为数列，记作xn=f(n) 或{xn}.xn称为通项（一般项） 2,4,82.,2”,. 2”} 111 2’4’8, 1,-1,1,.,(-1)m1,. (-1)”-1} 4E0:+少 ’3 √3，V3+√3，.，V3+V3+V.+V3,. HIGH EDUCATION PRESS

定义: 自变量取正整数的函数称为数列, 记作 或 称为通项(一般项) . 2,4,8,  ,2 , ; n , ; 2 1 , , 8 1 , 4 1 , 2 1  n  {2 } n } 2 1 { n 1, 1,1, ,( 1) , ; −  − n+1  {( 1) } −1 − n , ; ( 1) , , 3 4 , 2 1 2, 1   n n n− + − } ( 1) { 1 n n n− + − 3, 3 + 3,  , 3 + 3 + + 3 , 

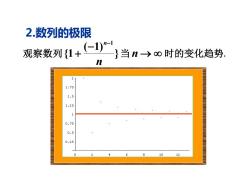
2数列的极限 观察数列1+一) 一}当n→oo时的变化趋势. n 1.75 1.5 1.25 0.75 0.5 0.25 10 12

观察数列 当 →  时的变化趋势. − + − n n n } ( 1) {1 1 2.数列的极限

定义：如果当无限增大时，数列{x,的通项xm 无限趋近于某一确定常数a,则称a为数 列{x,},当n趋于无穷大时的极限，记作 imxn三4，或xm→4(n→o） 1->oo 此时也称该数列收敛； 若不存在，则称数列发散。 HIGH EDUCATION PRESS

定义：如果当 n 无限增大时，数列  xn  的通项 n x 无限趋近于某一确定常数 a ，则称 a 为数 lim = , → ( → ) → xn a n a n n 或 x 此时也称该数列收敛； 若 a 不存在，则称数列发散。 列  xn  ，当 n 趋于无穷大时的极限，记作

例如， 123 2’34 n+1 →1(n→∞) n+1 143 2 n+(-1)-1 收 23’4 敛 xn=n+(-1)- →1(n→∞) n 2,4,8,.,2”, xn=2n>0(n→o) 发 1,-1,1,.,(-1D+1,. 散 xn=(-1)+1 趋势不定 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例如,  , 1 , , 4 3 , 3 2 , 2 1 n + n +1 = n n xn →1 (n → ) n n x n n 1 ( 1) − + − = →1 (n → ) 2 , 4 , 8 ,  , 2 n ,  n n x = 2 →  (n → ) 1 ( 1) + = − n n x 趋势不定 收 敛 发 散 机动 目录 上页 下页 返回 结束

问题：当无限增大时，是否无限接近于某一 确定的数值？如果是如何确定？ 通过上面演示实验的观察： 当m无限增大时，x,=1+H 无限接近于1. 问题：“无限接近”意味着什么？如何用数学语言 刻划它. HIGH EDUCATION PRESS 机动目录上页下页返回结束

问题: 当 无限增大时, 是否无限接近于某一 确定的数值?如果是,如何确定? n n x 1. ( 1) , 1 1 当 无限增大时 无限接近于 n n x n n − − = + 问题: “无限接近”意味着什么?如何用数学语言 刻划它.  xn − 1 = n n n 1 1 ( 1) 1 − = − 通过上面演示实验的观察: 机动 目录 上页 下页 返回 结束

下面用一个过程说明无限接近 给定 0由00只要a>10，有.-110 给定 1000 只要>10时、有x.-1小00 给定 b只要a>10o0时.有K.-10，只要n>N(=时，有x,-1<e成立， HIGH EDUCATION PRESS 机动目录上页下页返回结束

, 100 1 给定 , 100 1 1  n 由 只 要 n  100时, , 100 1 有 xn − 1  , 1000 1 给定 只 要 n  1000时, , 10000 1 , 有 xn − 1  10000 1 给定 只 要 n  10000时, , 1000 1 有 xn − 1  给定   0, ]) , 1 只要 ( [ 时  n  N = 有 − 1  成 立. n x 机动 目录 上页 下页 返回 结束 下面用一个过程说明无限接近

定义 如果对于任意给定的正数（不论它多么 小)，总存在正数N,使得对于n>N时的一奶m, 不等式xm一4<都成立，那末就称常数是数列 xm的极限，或者称数列x,收敛于，记为 lim x,=a,或xn→a(n-→o). n-→co 如果数列没有极限，就说数列是发散的 注意：1.不等式xm-a<ε刻划了xn与a的无限接近； 2.N与任意给定的正数ε有关， HIGH EDUCATION PRESS 机动目录上页下页返回结束

定 义 如果对于任意给定的正数 (不论它多么 小),总存在正数N ,使得对于n  N 时的一切xn , 不等式 x − a   n 都成立,那末就称常数a 是数列 xn的极限,或者称数列xn 收敛于a ,记为 lim x a, n n = → 或x → a (n → ). n 如果数列没有极限,就说数列是发散的. 注意： 1.不等式 x a 刻划了x 与a的无限接近; n n −   2.N与任意给定的正数有 关. 机动 目录 上页 下页 返回 结束

e-N定义：limx=a⊙ n→0 Ve>0,N>0,当n>N时，恒有xn-aN时，所有的点x都落在(a-6,a+)内， 只有有限个（至多只有N个）落在其外 HIGH EDUCATION PRESS 机动目录上页下页返回结束

x x2 x1 N + 2 x N +1 x x3 几何解释: 2 a −  a +  a , ( , ) , n 当n N x a a  − + 时 所有的点 都落在   内  − N定 义 : 其中  : 每一个或任给的;  : 至少有一个或存在. 0, 0, , . N n N x a n      −    当 时 恒有 只有有限个 ( ) . 至多只有N个 落在其外 机动 目录 上页 下页 返回 结束 lim n n x a →  = 