《线性代数》课程教学课件（PPT讲稿，B）第三章 矩阵的运算 §3.2 逆矩阵

第三章矩阵的运算 §3.2 逆矩阵 概念的引入 逆矩阵概念与性质 典型例题

第三章 矩阵的运算 §3.2 逆矩阵 一、概念的引入 二、逆矩阵概念与性质 三、典型例题

第三章矩阵的运算 、 概念的引入 在数的运算中，当数a≠0时，有 aa-=aa=1 其中=1为a的倒数，（或称a的逆）； 在矩阵的运算中，单位阵E相当于数的乘法运算 中的1，那么，对于矩阵A,如果存在一个矩阵A1, 使得 AA-=AA=E, 则矩阵A称为A的可逆矩阵或逆阵

第三章 矩阵的运算 , 1 1 AA  A A  E   则矩阵 称为A 的可逆矩阵或逆阵. 1 A 1, 1 1     aa a a 在数的运算中，当数a  0时，有 a a 1 1  其中  为a 的倒数，（或称 a 的逆）； 在矩阵的运算中，单位阵E相当于数的乘法运算 中的1，那么，对于矩阵A，如果存在一个矩阵A-1 , 使得 一 、概念的引入

第三章矩阵的运算 二、逆矩阵的概念与性质 定义3.2.1设A是一个阶方阵，若存在n阶方阵B, 使得 AB=BA=E 则称A可逆的，并称B为A的逆矩阵 如4[处引=[3月 有AB=BA=E,所以A与B互为逆阵

第三章 矩阵的运算 定义3.2.1 设A是一个n阶方阵，若存在n阶方阵B， 使得 AB = BA = E 则称 A 可逆的，并称B 为 A 的逆矩阵. 二、逆矩阵的概念与性质 1 2 5 2 , 2 5 2 1 A B                例如 有AB = BA = E ，所以A 与 B 互为逆阵

第三章矩阵的运算 说明若A是可逆矩阵，则A的逆矩阵是唯一的。 若设B和C是A的可逆矩阵，则有 AB=BA=E.AC=CA=E 可得B=EB=(CA)B=C(AB)=CE=C. 所以A的逆矩阵是唯一的，记作A1 B=C=A-

第三章 矩阵的运算 说明 若A是可逆矩阵，则A的逆矩阵是唯一的. 若设B和C是A的可逆矩阵，则有 AB  BA  E, AC  CA  E, 可得 B  EB  CAB  CAB  CE  C. 所以A的逆矩阵是唯一的,记作A-1 1 B C A .   

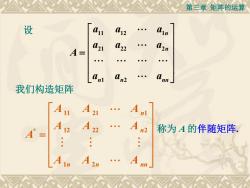
第三章矩阵的运算 设 12 421 A= 2 An 2 我们构造矩阵 A21 A A 2 称为A的伴随矩阵. : A A nn

第三章 矩阵的运算 我们构造矩阵 11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A              称为 A 的伴随矩阵. 设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a              

第三章矩阵的运算 由于 Al i=j 4,A+aa4++a.An=0 i≠i 可得： g+4,++0uAy=17 i≠i 0 0 0 14I 0 AA=AA- . -AE 。 0 0 . [A1 只要A≠0，就有()=（有4）A=E

第三章 矩阵的运算 可得： * * | | 0 0 0 | | 0 0 0 | | A A AA A A A E A                 1 1 2 2 1 1 2 2 0 0 i j i j in jn i j i j ni nj A i j a A a A a A i j A i j a A a A a A i j                     由于 1 * 1 * A 0 A( A ) ( A )A E A A 只要  ，就有  

第三章矩阵的运算 定理3.2.1（可逆的充分必要条件） n阶方阵A可逆一A≠0，而且A1 A 证明 ""(充分) 已证 "→"（必要） 若A可逆，则存在A1,使得AA1=E 两边取行列式，得|AA1=A‖A1=E=1 所以 A≠0

第三章 矩阵的运算 定理3.2.1（可逆的充分必要条件） . | | 1 | | 0 1     A A n阶方阵 A可逆 A ，而且 A 证明 ""(充分) 已证. ""(必要) 1 1 A A AA E   若 可逆，则存在 ，使得  两边取行列式，得 1 1 | AA | | A || A | | E | 1      所以 | A| 0

第三章矩阵的运算 推论 若A是n阶矩阵，且存在n阶矩阵B,使 AB=E或BA=E 则A可逆，且B为A的逆矩阵， 证明： 设AB=E 则|AB=|A‖B=|E=1 所以|A卡0，由定理可知，A可逆， 设其逆矩阵为A1,则有 B=EB=(A-A)B=A-(AB)=A-E=A 同理可证，若BA=E,则B=~1

第三章 矩阵的运算 推论 若A是n阶矩阵，且存在n阶矩阵B，使 AB=E 或 BA=E 则A可逆，且B为A的逆矩阵. 证明： 设AB=E 则 | AB || A|| B || E | 1 所以 | A| 0, 由定理可知，A可逆. 设其逆矩阵为A-1 ,则有 B  EB  1 (A A)B  1 A (AB)   1 A E   同理可证，若BA=E，则 1 B A .   1 A  

第三章矩阵的运算 12 -1 例1判断A= 3 0 是否可逆？若可逆，求其逆矩阵 -10 -2 解： 由于A=9≠0，故A可逆，又 A1=-2,A2=4,A31=4, A12=-2,A22=-3,A32=-3 A13=1,A23=-2,A33=-5, 2 1 于是 9 9 9 「-2 4 1 1 -3 -3 二3 3 3 5 1 2

第三章 矩阵的运算 1 2 1 1 3 1 0 . 1 0 2 A          例 判断 是否可逆？若可逆，求其逆矩阵 解： 由 于 A  9  0， 故 A 可逆，又 A11=-2， A21=4， A31=4， A12=-2， A22=-3， A32=-3 A13=1， A23=-2 ， A33=-5 ， 于是 1 * 2 4 1 1 1 6 3 3 9 1 2 5 A A A                2 4 1 9 9 9 2 1 1 3 3 3 1 2 5 9 9 9           

第三章矩阵的运算 逆矩阵的性质 (1)若A可逆，则4，A亦可逆，且 (A1)1=A,(A1=(A1) (2)若A可逆，数入≠0，则2A可逆，且 = (3)若A,B均可逆，则AB亦可逆，且 (AB)1=B1A1

第三章 矩阵的运算 逆矩阵的性质   1 1 1 1 1 1 , , , ( ) , ( ) ( ) . A A A A A A A           若 可逆 则 亦可逆 且     1 1 2 , 0, , 1 . A A A A         若 可逆 数 则 可逆 且   1 1 1 3 , , , ( ) A B AB AB B A     若 均可逆 则 亦可逆 且