《高等数学》课程教学资源（PPT课件）9.3全微分

第三节 第九章 全微分 元函数y=f(x)的微分 Ay=A△x+O(△x) dy=f"(x)△x应甩 近似计算 估计误差 本节内容： 一、 全微分的定义 二、全微分在数值计算中的应用 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第九章 *二、全微分在数值计算中的应用 应用 第三节 一元函数 y = f (x) 的微分 y = Ax + o(x) dy = f (x)x 近似计算 估计误差 机动 目录 上页 下页 返回 结束 本节内容: 一、全微分的定义 全微分

一、全微分的定义 定义：如果函数z=f(x,y在定义域D的内点(x,y) 处全增量△z=f(x+△x,y+△y)-f(x,y)可表示成 △：=A△x+B△y+o(p),p=V(△x)2+(△) 其中A,B不依赖于△x,△y,仅与x,y有关，则称函数 f(x,y)在点(x,y)可微，A△x+B△y称为函数f(x,y) 在点x,y)的全微分，记作 dz=df=A△x+B△y 若函数在域D内各点都可微，则称此函数在D内可微 HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、全微分的定义 定义: 如果函数 z = f ( x, y )在定义域 D 的内点( x , y ) 可表示成  z = Ax + B y + o( ) , 其中 A , B 不依赖于 x ,  y , 仅与 x , y 有关， 称为函数 f (x, y) 在点 (x, y) 的全微分, 记作 dz = d f = Ax + By 若函数在域 D 内各点都可微, 则称函数 f ( x, y ) 在点( x, y) 可微， 机动 目录 上页 下页 返回 结束 处全增量 则称此函数在D 内可微. A x B y  + 

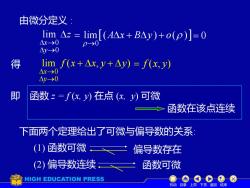
由微分定义： lim△z=lim[(A△x+B△y)+o(p)]=0 △x→0 D→0 △y-→0 得 limf(x+△x,y+△y)=f(x,y） △x>0 △y→0 即 函数z=f(x,y)在点（化，y)可微 函数在该点连续 下面两个定理给出了可微与偏导数的关系： (1)函数可微 偏导数存在 (2)偏导数连续，三 函数可微 HIGH EDUCATION PRESS 机动目 下页返回结

(2) 偏导数连续 z = f (x + x, y + y) − f (x, y) lim( ) ( ) 0   = Ax + By + o → 下面两个定理给出了可微与偏导数的关系: (1) 函数可微 函数 z = f (x, y) 在点 (x, y) 可微 lim ( , ) 0 0 f x x y y y x +  +   →  → 由微分定义 : 得 z y x   →  → 0 0 lim = 0 = f (x, y) 函数在该点连续 机动 目录 上页 下页 返回 结束 偏导数存在 函数可微 即

定理1（必要条件）若函数z=f(化，y)在点x,y)可微， 则该函数在该点偏导数 二2必存在，且有 Ox'Oy dz= 0-Ax+ O O2 Ly 证：由全增量公式△z=A△x+B△y+o(P),令△y=0 得到对x的偏增量 △x2=f(x+△x,y)-f(x,y)=A△x+o(△x Oz lim △x2=A △x→0△X 同样可证 =B,因此有dz= x*0y 02 Ly 8y Ox HIGH EDUCATION PRESS 机动目录上页下页返回结束

定理1(必要条件) 若函数 z = f (x, y) 在点(x, y) 可微 , 则该函数在该点偏导数 y y z x x z z     +   d = x z    同样可证 B, y z =   证: 由全增量公式 令y = 0, = Ax + o( x ) 必存在,且有 得到对 x 的偏增量 x + x x 因此有 x zx x   =  →0 lim = A 机动 目录 上页 下页 返回 结束

注意：定理1的逆定理不成立.即： 偏导数存在函数不一定可微！ 反刷：函数儿，列 ，x2+y2≠0 x2+y2=0 易知f(0,0)=f,0,0)=0,但 A-.(0.0)Ax+f,0,0)A=Ax+A △x△y △x△y △x△y 2+apx+ 0 ≠o(P)因此，函数在点(0,0)不可微 HIGH EDUCATION PRESS 机动目录上贡下页返回结束

反例: 函数 f (x, y) = 易知 (0, 0) = (0, 0) = 0 , x y f f 但 z [ f ( 0, 0) x f ( 0, 0) y]  − x  + y   o( ) 因此,函数在点 (0,0) 不可微 . 注意: 定理1 的逆定理不成立 . 2 2 ( x) ( y) x y  +    = 2 2 ( x) ( y) x y  +    = 0 偏导数存在函数 不一定可微 ! 即: , 0 2 2 2 2 +  + x y x y xy 0, 0 2 2 x + y = 机动 目录 上页 下页 返回 结束

定理2（充分条件）若函数z=f(x,y)的偏导数 da Ox ay 在点(x,y)连续，则函数在该点可微分 不证：△z=f(x+△x,y+△y)-f(xy) =[f(x+△x,y+Ay)-f(x,y+△y】 +[f(x,y+△y)-f(x,y] f(x+0Ax,y+Ay)Ax+f (x,y+02A))Ay 00 HIGH EDUCATION PRESS 机动目录上页下页返回结束

=[ f (x + x, y + y) ] 定理2 (充分条件) y z x z     , 不证： z = f (x + x, y + y) − f (x, y) (0 , 1) 1  2  f x y x = [ x ( , ) + ]       f x y y y = f x (x +1x, y + y)x + y ( , + 2 ) − f (x, y + y) +[ f (x, y + y ) − f (x, y)] f x y y +[ y ( , ) + ] 若函数 的偏导数 在点(x, y) 连续, 则函数在该点可微分.   机动 目录 上页 下页 返回 结束 lim 0 0 0 =  →  →  y x lim 0, 0 0 =  →  →  y x

△z=: =f(x,y)△x+fv(x,y)△y+C△x+阝△y =0.=0 △x>0 △x>0 Ay→0 △y→0 注意到 2y斗a故有 正=fx(x,y)△x+f(x,y)Ay+o(p) 所以函数z=f(x,y)在点(x,y)可微 HIGH EDUCATION PRESS 机动目录上页下页返回结束

z = f x y x f x y y = x ( , ) + y ( , ) z f x y x f x y y  = x ( , ) + y ( , )       + x + y 所以函数 + x +  y 在点 可微. 机动 目录 上页 下页 返回 结束       lim 0 0 0 =  →  →  y x lim 0, 0 0 =  →  →  y x 注意到 , 故有 + o( )

例2.计算函数z=ey在点(2,1)处的全微分 解： =xexy Ox 0y =e2, 0z 2,1) a(2,0 2e2 dz -e2dx+2e2dy=e2(dx+2dy) (2,1D 例3.计算函数u=x+sin二+e'z的全微分 解：du=1dx+(cos5+zey)dy+yedz HIGH EDUCATION PRESS 机动目录上页下页返回结束

例2. 计算函数 在点 (2,1) 处的全微分. 解: =   x z 2 2 2 (2,1) , (2,1) e y z e x z =   =   例3. 计算函数 的全微分. 解: d u = y y ( cos )d 2 2 1 + =   y z , xy ye xy xe y z z e 机动 目录 上页 下页 返回 结束

·二、全微分在数值计算中的应用（不讲） 1.近似计算 由全微分定义 Az=f(x,y)Ax+f(x,y)Ay+o(p) dz 可知当△x及△y较小时，有近似等式 △2≈dz=f(x,y)Ax+f(x,y)Ay (可用于近似计算，误差分析) f(x+Ax,y+Ay)f(x,y)+f(x,y)Ax+fy(x,y)Ay (可用于近似计算) HIGH EDUCATION PRESS 机动目 下页返回结束

可知当 *二、全微分在数值计算中的应用(不讲) 1. 近似计算 由全微分定义 z f (x, y) x f (x, y) y o()  = x  + y  + f (x + x, y + y) f x y x f x y y x ( , ) + y ( , ) 较小时, z z f x y x f x y y   d = x ( , ) + y ( , ) d z 及 有近似等式:  f (x, y) + 机动 目录 上页 下页 返回 结束 (可用于近似计算; 误差分析) (可用于近似计算)

例3.有一圆柱体受压后发生形变，半径由20cm增大 到20.05cm,高度由100cm减少到99cm,求此圆柱体 体积的近似改变量， 解：已知V=πr2h,则 △V≈2πrh△r+πr2△h r=20,h=100 △r=0.05,△h=-1 △V≈2元x20×100×0.05+π×202×(-1) =-200π(cm3) 即受压后圆柱体体积减少了200mcm HIGH EDUCATION PRESS 机动目录上页下页返回结束

半径由 20cm 增大 解: 已知 V  r = 20, h =100, 2 20 100 0.05 20 ( 1) 2 V      +   − 即受压后圆柱体体积减少了 例3. 有一圆柱体受压后发生形变, 到 20.05cm , 则 2 rhr + r h 2  r = 0.05, h = −1 200 (cm ) 3 = −  高度由100cm 减少到 99cm , 体积的近似改变量. 机动 目录 上页 下页 返回 结束 求此圆柱体