《高等数学》课程教学资源（PPT课件）9.6多元函数微分学的几何应用

第之节 第九章 多元蓝数微分学的儿何应用 、一元向量值函数及其导数 二、空间曲线的切线与法平面 三、曲面的切平面与法线 HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 二、空间曲线的切线与法平面 第六节 一、一元向量值函数及其导数 三、曲面的切平面与法线 多元函数微分学的几何应用 第九章

一、 一元向量值函数及其导数 引例：已知空间曲线的参数方程： x=0(t) y= w(t) t∈[a,β] z=0(t) 记7=(x,y,z),f()=(p(1),w(t),o(t) T的向量方程：7=f(),1∈[a,] 此方程确定映射f:Iα，β]→R,称此映射为一元向量 值函数， 对T上的动点M,显然=OM,即T是r的终点M 的轨迹，此轨迹称为向量值函数的终端曲线 要用向量值品数研究曲孩的莲猿性和光滑性，就需要引进向 量值画数的极限、连续和导数的概念 HIGH EDUCATION PRESS O0 目录上页下页返回结束

目录 上页 下页 返回 结束 一、一元向量值函数及其导数 引例: 已知空间曲线  的参数方程: [ , ] ( ) ( ) ( )           = = = t z t y t x t 记 r = (x, y,z), f (t) = ((t),(t),(t))  的向量方程： r = f (t), t [,] M r  x z O y 对 上的动点M , 即 是 此方程确定映射 3 f :[,]→ R ,称此映射为一元向量 显然r = OM， r 的终点M 的轨迹 , 此轨迹称为向量值函数的终端曲线 . 值函数. 要用向量值函数研究曲线的连续性和光滑性，就需要引进向 量值函数的极限、连续和导数的概念

定义1：给定数集DcR,称映射f:D→R”为一元向量 值函数（简称向量值函数），记为 定义域 7=f(t),1∈D 因变量 自变量 0 定义2：设f(t)=(f(t),f2(t),f3(t),t∈U(o), O∈R3 若V8>0,38>0,使得当0t-toKδ时，有|f(t)-0K8, 则%称为f(t)当t→to时的极限，记作 imf)=元或fa)→元，t→0 注：极限：mf(=mf(,1m(,m/》 t 连续：limf0)=f, HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 定义1: 给定数集 D  R , 称映射 n f : D → R 为一元向量 值函数（简称向量值函数）, 记为 r = f (t), t  D 定义域 因变量 自变量 注：极限： 连续： lim ( ) (lim ( ), lim ( ), lim ( )) 1 2 3 0 0 0 0 f t f t f t f t t→t t→t t→t t→t = lim ( ) ( ) 0 0 f t f t t t = → 定义2: 设 3 0 0 0 1 2 3 f (t) = ( f (t), f (t), f (t)), t U(t ), r  R 0, 0, 0 | | | ( ) | , 0 0 若    使得当  t −t   时，有 f t − r   则r0 称为 f (t)当t → t 0 时的极限，记作 0 0 0 lim ( ) ( ) , 0 f t r f t r t t t t = → → → 或

定义3：设 f(u),teU(o)。 若lim △r lim 7o+△)-2存在 t->to△t t→to △t 则此极限称为f(t)在to处的导数或导向量，记作 (o)或 di t=to 注：导数：f()=(f'(t),f2'(1),f3'() HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 定义3: 设 ( ), ( ), 0 f t t U t 若 存在 t f t t f t t r t t t t  +  − =   → → ( ) ( ) lim lim 0 0 0 0 则此极限称为 f (t)在t 0 处的导数或导向量，记 作 0 '( ) 0 t t dt dr f t =  或 注：导数： '( ) ( '( ), '( ), '( )) 1 2 3 f t = f t f t f t

向量值函数的导数运算法则：P94) 设，下是可导向量值函数，C是常向量，c是任一常数 (t)是可导函数，则 (ac-o (2)[ci(u]=ci() (3)d[i0)±】=()士(0) (4)↓Lp)i】=p'(u)i0）+p()i() (5)0)=)0)+) (6)母，[i)×】=0x0)+)x0 (7) p(t]=p'(a)Lo(t)] d t HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 向量值函数的导数运算法则: (P94) 设 u, v 是可导向量值函数, (t) 是可导函数, 则 C O t = d d (1) (2) [ ( )] ( ) d d cu t c u t t =  (3) [ ( ) ( )] ( ) ( ) d d u t v t u t v t t  =    (4) [ ( ) ( )] ( ) ( ) ( ) ( ) d d t u t t u t t u t t  = +  (5) [ ( ) ( )] ( ) ( ) ( ) ( ) d d u t v t u t v t u t v t t  =   +   (6) [ ( ) ( )] ( ) ( ) ( ) ( ) d d u t v t u t v t u t v t t  =   +   C 是常向量, c 是任一常数, (7)  ( ) ( )  ( ) d d u t t u t t  =  

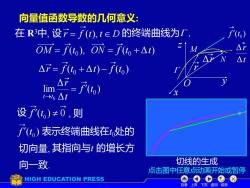
向量值函数导数的几何意义： 在R中，设7=f(d),t∈D的终端曲线为I, t OM=f),ON=f。+△) △T=f。+△)-f,) lim =F() →0△t 设f()≠0，则 f(,)表示终端曲线在处的 切向量，其指向与t的增长方 向一致 切线的生成 点击图中任意点动画开始或暂停 HIGH EDUCATION PRESS eOC①8 目录上页下页返回结束

目录 上页 下页 返回 结束 向量值函数导数的几何意义: 在 R3中, 设 r = f (t), t  D 的终端曲线为 , 切线的生成 点击图中任意点动画开始或暂停 M  x z O y Δr ( )0 f  t t r Δ Δ ( ), ( Δ ) 0 0 OM = f t ON = f t + t N Δ ( Δ ) ( ) 0 0 r = f t + t − f t ( ) Δ Δ lim 0 0 f t t r t t =  → 表示终端曲线在t0处的 切向量, 其指向与t 的增长方 向一致. ( )0 f  t 设 f (t 0 )  0 , 则 r

向量值函数导数的物理意义： 设亓=f(1)表示质点沿光滑曲线运动的位置向量，则有 速度向量：0=f) 加速度向量：a=(0)=() 例1.设f)=(cos)i+(sin)j+1k,求1imf) 解：limf()=(lim cos)i+(imsin)j+limt无 7+2+e) HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 向量值函数导数的物理意义: 设 r = f (t) 表示质点沿光滑曲线运动的位置向量, 则有 v(t) = f (t) a = v (t) = f (t) ( ) (cos ) (sin ) , lim ( ). 4 π f t t i t j t k f t t→ 例1. 设 = + + 求 速度向量： 加速度向量： 解： f t t i t j t k t t t t 4 π 4 π 4 π 4 π lim ( ) (lim cos ) (limsin ) lim → → → → = + + i j k 4 π 2 2 2 2 = + + ( ( ) ) 4 π = f

例2.设空间曲线厂的向量方程为 7=ft)=(2+1,4t-3,2-6),1∈R 求曲线T上对应于1。=2的点处的单位切向量 解：f"()=(2i,4,4t-6),teR f'(2)=(4,4,2) 7(2)=V42+42+22=6 故所求单位切向量为 其方向与t的增长方向一致 另一与1的增长方向相反的单位切向量为(-？-乙 HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 例2. 设空间曲线 的向量方程为 求曲线 上对应于 解: ( ) ( 1, 4 3, 2 6 ) 2 2 r = f t = t + t − t − t 的点处的单位切向量. 故所求单位切向量为 其方向与 t 的增长方向一致 另一与 t 的增长方向相反的单位切向量为 ) 3 1 , 3 2 , 3 2 (− − −

例3.一人悬挂在滑翔机上，受快速上升气流影响作螺 旋式上升，其位置向量为7=(3cost,3simt,t),求 (1)滑翔机在任意时垓刻t的速度向量与加速度向量 (2)滑翔机在任意时刻1的速率 (3)滑翔机的加速度与速度正交的时刻 解：(1)下=7(t)=(-3sint,3c0s1,20 a==(-3cost,-3sint,2) (2) r(t)=V(3sin)2+(-3cos)2+(2r)2=9+4 (3)由v.a=0即9 sintcost-9 costsint+4t=0, 得t=0,即仅在开始时该刻滑翔机的加速度与速度正交 HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 例3. 一人悬挂在滑翔机上, 受快速上升气流影响作螺 旋式上升, 其位置向量为 求 (1) 滑翔机在任意时刻 t 的速度向量与加速度向量; (2) 滑翔机在任意时刻 t 的速率; (3) 滑翔机的加速度与速度正交的时刻. 解: (1) (3) 由 即 得t = 0, 即仅在开始时刻滑翔机的加速度与速度正交

二、空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限位 置、过点M与切线垂直的平面称为曲线在该点的法平面. 给定光滑曲线 I:f(t)=(p(t),w(t),@(t)) 则当o,wo'不同时为0时，T在 点M(化，yz)处的切向量及法平面的 法向量均为 f'(1)=(0'(),W(1),o'(t) 点向式可建立曲线的切线方程 利用 点法式可建立曲线的法平面方程 HIGH EDUCATION PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 二、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法平面.  T M  置. 空间光滑曲线在点 M 处的切线为此点处割线的极限位 ：f (t) = ((t), (t),(t)) 给定光滑曲线  在 f (t) = ((t),(t),(t)) 点法式可建立曲线的法平面方程 利用 则当 ， ，不同时为 0时， 点M (x, y, z) 处的切向量及法平面的 法向量均为 点向式可建立曲线的切线方程