《高等数学》课程教学资源（PPT课件）12.3幂级数

第三节 第十二章 幂级数 函数项级数的概念 二、 幂级数及其收敛性 三、幂级数的运算 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第三节 一、函数项级数的概念 二、幂级数及其收敛性 三、幂级数的运算 幂级数 机动 目录 上页 下页 返回 结束 第十二章

一、 函数项级数的概念 设4n(x)(n=1,2,.)为定义在区间1上的函数，称 ∑n(x)=4(x)+42(x)+.+4n(x)+. n=1 为定义在区间】上的函数项级数 对x∈I,若常数项级数∑4n(xo)收敛，称x为其收 n=l 敛点，所有收敛点的全体称为其收敛域 若常数项级数∑u,(xo)发散，称x,为其发散点，所有 n=l 发散点的全体称为其发散域 HIGH EDUCATION PRESS 下页返回结束

一、 函数项级数的概念 设 为定义在区间 I 上的函数项级数 . 对 若常数项级数 敛点, 所有收敛点的全体称为其收敛域 ; 若常数项级数 为定义在区间 I 上的函数, 称 收敛, 发散 , 所有 0 称 x 为其收 0 称x 为其发散点, u (x) (n =1,2, ) n 发散点的全体称为其发散域 . 机动 目录 上页 下页 返回 结束

在收敛域上，函数项级数的和是x的函数S(x),称它 为级数的和函数，并写成 00 S)=∑4) n=1 若用Sn(x)表示函数项级数前n项的和，即 S,()=Σ4(x) k=1 令余项rn(x)=S(x)-Sn(x) 则在收敛域上有 lim S,(x)=S(x),lim(x)=0 n→00 n→00 HIGH EDUCATION PRESS 机动目录上页下页返回结束

为级数的和函数 , 并写成 若用 令余项 则在收敛域上有 表示函数项级数前 n 项的和, 即 在收敛域上, 函数项级数的和是 x 的函数 称它 机动 目录 上页 下页 返回 结束

例如，等比级数 ∑x”=1+x+x2+.+x”+ n=0 它的收敛域是(-1,1)，当x∈(-1,1)时，有和函数 1 1-x n=0 它的发散域是(-∞，-1]及[1，+∞)，或写作x≥1 又如，级数 心x”十x (x≠0)，当x=1时收敛， n=0 但当0<x≠1时，1imun(x)=o,级数发散； 所以级数的收敛域仅为x=1. HIGH EDUCATION PRESS 机动目 下页返回结束

例如, 等比级数 它的收敛域是 它的发散域是 (− , −1]及[1，+ ）, 或写作 x 1. 又如, 级数 级数发散 ; 所以级数的收敛域仅为 有和函数 机动 目录 上页 下页 返回 结束

二、幂级数及其收敛性 形如 ∑a,(x-0)》”=a0+ax-x0)+a(x-xo)}+ .+an(x-xo)”+. 的函数项级数称为幂级数，其中数列an(n=0,1,)称 为幂级数的系数 下面着重讨论x,=0的情形，即 anx”=a0+ax+a2x2+tanx”+ n= 例如，幂级数 x”=x<1即是此种情形 n=( HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、幂级数及其收敛性 形如 的函数项级数称为幂级数, 其中数列 下面着重讨论 例如, 幂级数 , 1 1 1 0  −  =  = x x x n n 为幂级数的系数 . 即是此种情形. 的情形, 即 称 机动 目录 上页 下页 返回 结束

定理1.(Abel定理)若幂级数 n=0 在x=0点收敛，则对满足不等式xxo的一切x,该幂级数也发散 证：设∑anx收敛，则必有1 im ax6=0,于是存在 n=0 n-→00 常数M>0,使 M(n=1,2,.) 收敛发散 发 散 收0敛 发散 HIGH EDUCATION PRESS 阿贝尔目录上页下页返回结束

发 散 收 o 敛 发 散 x 收敛 发散 定理 1. ( Abel定理 ) 若幂级数   n=0 n n a x 则对满足不等式 的一切 x 幂级数都绝对收敛. 反之, 若当 的一切 x , 该幂级数也发散 . 时该幂级数发散 , 则对满足不等式 证: 设 收敛, 则必有 于是存在 常数 M > 0, 使 阿贝尔 目录 上页 下页 返回 结束

g,=aa”sM 当xo且使级数收敛，则由前 面的证明可知，级数在点x。也应收敛，与所设矛盾 故假设不真所以若当x=x,时幂级数发散，则对一切 满足不等式x>xo的x,原幂级数也发散. 证毕 HIGH EDUCATION PRESS Oe0C08 机动目录上页下页返回结束

当 x  x0 时, 收敛, 故原幂级数绝对收敛 . 也收敛, 反之, 若当 0 x = x 时该幂级数发散 ,下面用反证法证之. 假设有一点 1 x 1 0 x  x 0 x 满足不等式 0 x  x 所以若当 0 x = x 满足 且使级数收敛 , 面的证明可知, 级数在点 故假设不真. 的 x , 原幂级数也发散 . 时幂级数发散 , 则对一切 则由前 也应收敛, 与所设矛盾, n n n n n n x x a x a x 0 = 0 n n n x x a x 0 0 =  证毕 机动 目录 上页 下页 返回 结束

由Abel定理可以看出， ∑anxn 的收敛域是以原点为 中心的区间 n=0 用±R表示幂级数收敛与发散的分界点，则 R=0时，幂级数仅在x=0收敛； R=∞时，幂级数在(-0，+o)收敛； 0<R<∞，幂级数在(-R,R)收敛，在[-R,R] 外发散，在x=±R可能收敛也可能发散 R称为收敛半径，(-R,R)称为收敛区间 (-R,R)加上收敛的端点称为收敛域 收敛发散 发 散 收0敛 发散 HIGH EDUCATION PRESS 机动目录上页下页返回结束

幂级数在 (－∞, +∞) 收敛 ; 由Abel 定理可以看出,   n=0 n n a x 中心的区间. 用±R 表示幂级数收敛与发散的分界点, 的收敛域是以原点为 则 R = 0 时, 幂级数仅在 x = 0 收敛 ; R =  时, 0  R   , 幂级数在 (－R , R ) 收敛 ; (－R , R ) 加上收敛的端点称为收敛域. R 称为收敛半径 ， 在[－R , R ] 外发散; 在 x = R 可能收敛也可能发散 . (－R , R ) 称为收敛区间. 发 散 收 o 敛 发 散 x 收敛 发散 机动 目录 上页 下页 返回 结束

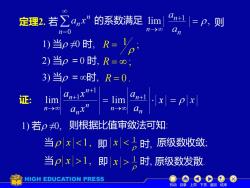
定理2.若∑anx” 的系数满足1im an|=p,则 n=0 an )当p0时，R=2 2)当p=0时，R=0； 3)当p=时，R=0 证： lim lim =pl anx" 1)若ρ0，则根据比值审敛法可知 当px1,即x>时，原级数发散 HIGH EDUCATION PRESS 机动目录上页下页返回结束

x a a a x a x n n n n n n n n =  + → + + → 1 1 1 lim lim 定理2. 若 的系数满足 1 ;  R = R =  ; R = 0 . 证: 1) 若 ≠0, 则根据比值审敛法可知: 当  x 1, 原级数收敛; 当  x 1, 原级数发散. 即  1 x  时, 1) 当 ≠0 时, 2) 当 ＝0 时, 3) 当 ＝∞时, 即 时, 则  1 x  机动 目录 上页 下页 返回 结束

因此级数的收敛半径R= 2)若P=0,则根据比值审敛法可知，对任意x原级数 绝对收敛，因此R=o; 3)若p=∞，则对除x=0以外的一切x原级发散 因此R=0」 说明据此定理 anx" 的收敛半径为R=lim n=0 n→0 An+l HIGH EDUCATION PRESS 机动目 下页返回结束

2) 若  = 0, 则根据比值审敛法可知, 绝对收敛 , R =  ; 3) 若  = , 则对除 x = 0 以外的一切 x 原级发散 , R = 0 . 对任意 x 原级数 因此 因此 的收敛半径为 说明:据此定理 1 lim + → = n n n a a R 因此级数的收敛半径 . 1  R = 机动 目录 上页 下页 返回 结束