《高等数学》课程教学资源（PPT课件）10.2二重积分的计算法

第二节 第十章 二重积分的汁算法 一、 利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、二重积分的换元法 HIGH EDUCATION PRESS 机动目录上页下页返回结束

*三、二重积分的换元法 第二节 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 机动 目录 上页 下页 返回 结束 二重积分的计算法 第十章

一、利用直角坐标计算二重积分 设曲顶柱的底为 y=P2(x) -,网到 任取xo∈[a,b],平面x=x截柱体的 截面积为 -r P(x) 故曲顶柱体体积为 V=∬nfx,)dc=∫Axx =j/cwd]a HIGH EDUCATION PRESS 机动目录上页下页返回结束

x b a [ ]d  = 设曲顶柱的底为           = a x b x y x D x y ( ) ( ) ( , ) 1  2 任取 平面 故曲顶柱体体积为  = D V f (x, y)d 截面积为 f x y y x x ( , )d ( ) ( ) 2 1     = b a A(x)d x 截柱体的 ( ) 2 y = x ( ) 1 y = x z x y o a x0 b D 机动 目录 上页 下页 返回 结束 一、利用直角坐标计算二重积分

同样，曲顶柱的底为 D={(x,y)w1(y)≤x≤Ψ2(y),c≤y≤d} 则其体积可按如下两次积分计算 V=∬nfx,yda x=V(y) x月2() -cd]ay dyrxt HIGH EDUCATION PRESS 机动目录上页下页返回结束

y d c o x ( ) 2 x = y ( ) 1 x = y y y d c [ ]d  = D = (x, y) 1 ( y)  x  2 ( y), c  y  d  同样, 曲顶柱的底为 则其体积可按如下两次积分计算  = D V f (x, y)d f x y x y y ( , )d ( ) ( ) 2 1     机动 目录 上页 下页 返回 结束

由曲顶柱体体积的计算可知，当被积函数f(x,y)≥0 且在D上连续时，若D为X-型区域 y计y=p2(x) p1(x)≤y≤02(x) a≤x≤b qay=o(x)b x 则 。xda-axga (y)≤x≤Ψ2(y) y x=W2(y) 若D为Y型区域D:esysd y 则2飞ud=afkd 等HIGH EDUCATION PRESS 机动目录上贡 下页返回结束

且在D上连续时, 当被积函数 f (x, y)  0        a x b x y x D ( ) ( ) : 1  2 D f (x, y)dxdy f x y y x x ( , )d ( ) ( ) 2 1     = b a d x 由曲顶柱体体积的计算可知, 若D为 X – 型区域 则 ( ) 1 y = x ( ) 2 y = x o b x y D a x 若D为Y –型区域        c y d y x y D ( ) ( ) : 1  2 y ( ) 1 x = y ( ) 2 x = y x d o c y f x y x y y ( , )d ( ) ( ) 2 1     d c 则 d y 机动 目录 上页 下页 返回 结束

当被积函数f(x,y)在D上变号时，由于 fx,)=3+x f(x,y)-f(x,y) 2 2 (x,y) f2(x,y)均非负 J∬nf(xy)dxdy=j∬n(x,y)dxdy -j∬nf2c,)dxdy 因此上面讨论的累次积分法仍然有效 HIGH EDUCATION PRESS 机动目录上页下页返回结束

当被积函数 f (x, y) − + = 2 ( , ) ( , ) ( , ) f x y f x y f x y 2 f (x, y) − f (x, y) ( , ) 1 f x y ( , ) 2 f x y 均非负 在D上变号时, 因此上面讨论的累次积分法仍然有效 . 由于 机动 目录 上页 下页 返回 结束

说明：(1)若积分区域既是X-型区域又是Y-型区域， 则有 J∬nfx,)drdy -d ol a b x 为计算方便，可选择积分序，必要时还可以交换积分序 (2)若积分域较复杂，可将它分成若干y X型域或Y-型域，则 川p=U+∬2+n HIGH EDUCATION PRESS 机动目 泉上页下页返回结束

o x y 说明: (1) 若积分区域既是X–型区域又是Y –型区域 , D f (x, y)dxdy 为计算方便,可选择积分序, 必要时还可以交换积分序. ( ) 2 y = x o x y D a b ( ) 1 x = y ( ) 2 x = y d c 则有 x ( ) 1 y = x y f x y y x x ( , )d ( ) ( ) 2 1     = b a d x f x y x y y ( , )d ( ) ( ) 2 1     = d c d y (2) 若积分域较复杂,可将它分成若干 D1 D2 D3 X-型域或Y-型域 ,     = + + D D1 D2 D3 则 机动 目录 上页 下页 返回 结束

例1.计算1=川Dxdo,其中D是直线y=1,x=2,及 y=x所围的闭区域 解法1.将D看作K型区域则D:Sy≤ 1≤x≤2 I-Pdxddx =[x2-x]x=8 解法2.将D看作Y型区域，则D: 「y≤x≤2 1≤y≤2 1=dx-7-2-8 HIGH EDUCATION PRESS 机动目录上页下页返回结束

x y 2 1 1 y = x o 2  = 2 1 dy 例1. 计算 d ,  = D I xy  其中D 是直线 y＝1, x＝2, 及 y＝x 所围的闭区域. x 解法1. 将D看作X–型区域, 则    D : I =  2 1 d x xyd y  = 2 1 d x    = − 2 1 2 3 1 2 1 x x dx 8 9 =   1 2 2 1 x xy 解法2. 将D看作Y–型区域, 则    D : I =  xyd x  2 1 d y   y x y 2 2 2 1    = − 2 1 3 2 1 2y y dy 8 9 = y 1 x y 2 1 y  x 1 x  2 y  x  2 1 y  2 机动 目录 上页 下页 返回 结束

例3.计算 八Dxdσ，其中D是抛物线y2=x及直线 y=x-2所围成的闭区域， 解：为计算简便，先对x后对y积分 则 y=X-2 JdG-Ldpdx =Lx2]2a=0+22-y1ay 3-22- HIGH EDUCATION PRESS 机动目录上页 下页返回结束

例3. 计算 d , D xy  其中D 是抛物线 所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分,    D :  xy d x  D xyd − = 2 1 dy   − + = 2 1 2 2 2 1 x y 2 dy y y − = + − 2 1 2 5 [ ( 2) ] d 2 1 y y y y D y = x 2 y = x − 2 2 −1 4 o y x y 2 2 y  x  y + −1 y  2 2 y y + 2 及直线 则 机动 目录 上页 下页 返回 结束

例4.求两个底圆半径为R的直角圆柱面所围的体积 解：设两个直圆柱方程为 x2+y2=R2,x2+z2=R2 利用对称性，考虑第一卦限部分， 其曲顶柱体的顶为z=√R2-x2 ()ED:05ysR2-x 0≤x≤R z2=R2 则所求体积为 -Raxdy-xd =8(R2-x2)dx=16R3 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例4. 求两个底圆半径为R 的直角圆柱面所围的体积. x y z R o R 解: 设两个直圆柱方程为 , 2 2 2 x + y = R 利用对称性, 考虑第一卦限部分, 其曲顶柱体的顶为 则所求体积为  − 2 2 0 d R x y R x x R 8 ( )d 0 2 2  = − 3 3 16 = R 2 2 2 x + z = R 2 2 z = R − x        −  0 0 ( , ) : 2 2 x R y R x x y D R x x R 8 d 0 2 2  = − 机动 目录 上页 下页 返回 结束

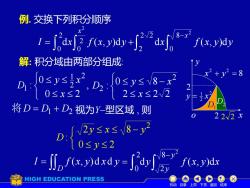
例.交换下列积分顺序 1=月fx+2a 解：积分域由两部分组成 12 =8 .0≤y≤ ≤y≤V8-x 2≤x≤22 将D=D1+D2视为Y-型区域，则 22/2 028y 0≤y≤2 1-∬，ady- f(x,y)dx HIGH EDUCATION PRESS 机动目录上页下页返回结束

例. 交换下列积分顺序     − = + 2 2 8 0 2 2 2 2 0 2 0 d ( , )d d ( , )d x x I x f x y y x f x y y 解: 积分域由两部分组成: , 0 2 0 : 2 2 1 1        x y x D 8 2 2 x + y = D2 2 2 y o 2 x D1 2 2 1 y = x 2        − 2 2 2 0 8 : 2 2 x y x D 将D = D1 + D2    D : 视为Y–型区域 , 则 2 2y  x  8 − y 0  y  2  = D I f (x, y)d xd y  − 2 8 2 ( , )d y y f x y x  = 2 0 dy 机动 目录 上页 下页 返回 结束